Browse By Unit
1.1 Introducing Calculus: Can Change Occur at An Instant?
1 min read•june 18, 2024
Welcome to AP Calculus! If you’re feeling nervous, don’t worry, we got your back. 🤗
Most of the math you have studied until this point was likely focused on functions with a constant rate of change, or you may have known it as “slope”. However, many equations that express real-world processes often do not have a constant rate of change throughout.
In fact, many functions change differently throughout their intervals, making it difficult to measure the rate of change at every single instant of a function. To simplify this process, we use the concept of limits to dynamically measure change between instances in a function.
Finding the Rate of Change
In AP Calculus AB/BC, we define slope as the rate of change between two points in a given function. Recall from your previous math classes that the slope formula is the change in y over the change in x.
By finding the change between two variables in a given interval, we can obtain the slope of the secant line of a function, which helps us understand the rate of change between two points in a given function. As you use different points to measure the rate of change in a function, you will see that the secant line changes constantly by having a different slope at different intervals, as demonstrated in the series of tangent lines in the image below:
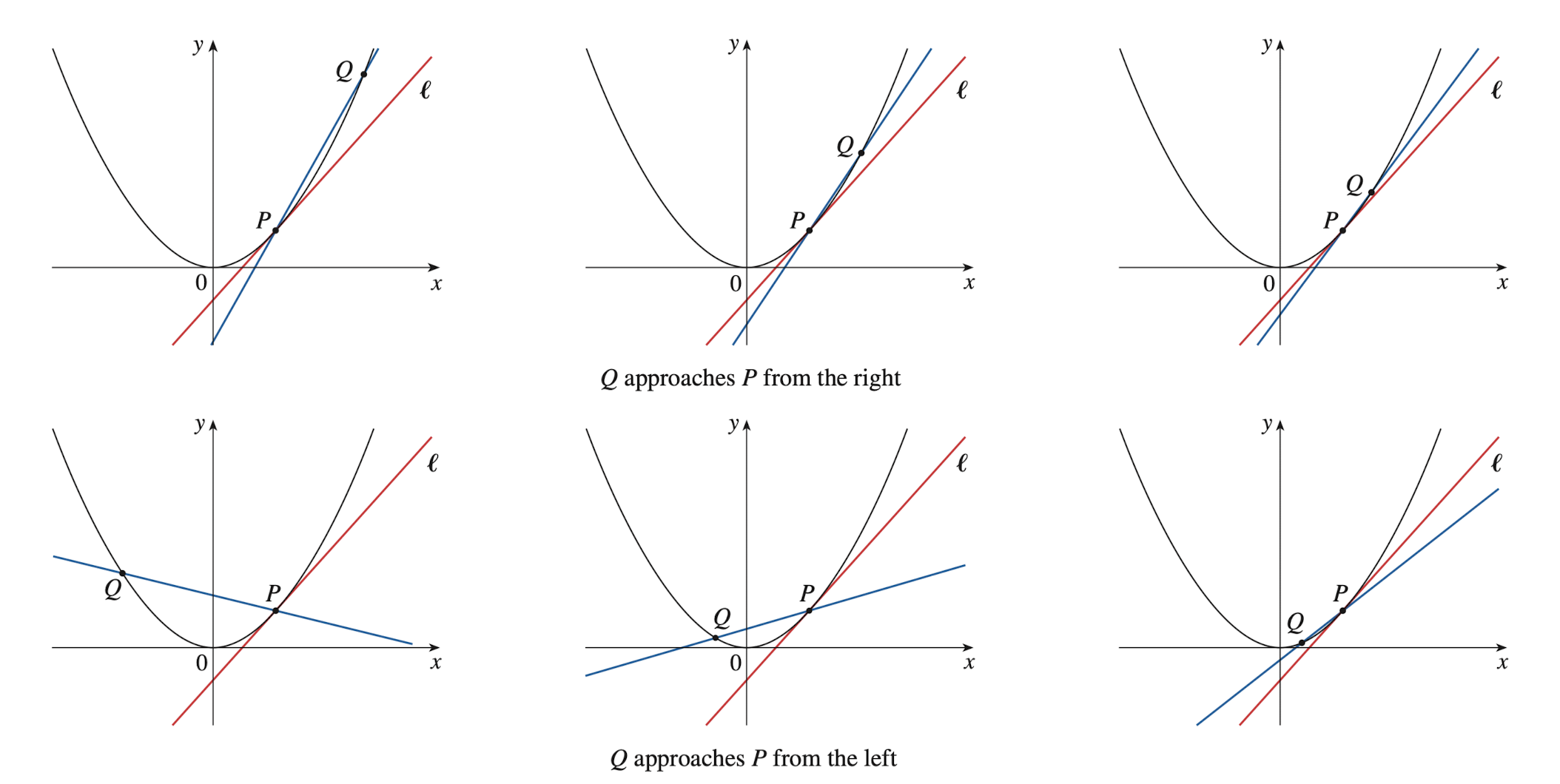
Courtesy of Calculus: Early Transcendentals by Larson and Edwards.
This image displays several secant lines of the same function. Notice how each of the secant lines has a distinct slope, which is the result of using different endpoints in the interval for measuring the rate of change.
Concept of Limits
So what are limits? Limits are going to be the focus of the first unit in this class.
Limits are expressions used to measure the rate of change at a given point. This is called the instantaneous rate of change, as it aims to find change at one particular point (for example, point a). Below is how a limit would be written and expressed mathematically:
It is important to note that due to the nature of the rate of change formula, the endpoints of the interval cannot be the same as they would result in a change of y over 0, which is undefined. In future lessons, you will use the definition of a limit to find the derivative, which is also known as the slope of the tangent line.
So…to answer the question, “can change occur at an instant?”, yes it can! Let’s get into limits further and define them.
<< Hide Menu
1.1 Introducing Calculus: Can Change Occur at An Instant?
1 min read•june 18, 2024
Welcome to AP Calculus! If you’re feeling nervous, don’t worry, we got your back. 🤗
Most of the math you have studied until this point was likely focused on functions with a constant rate of change, or you may have known it as “slope”. However, many equations that express real-world processes often do not have a constant rate of change throughout.
In fact, many functions change differently throughout their intervals, making it difficult to measure the rate of change at every single instant of a function. To simplify this process, we use the concept of limits to dynamically measure change between instances in a function.
Finding the Rate of Change
In AP Calculus AB/BC, we define slope as the rate of change between two points in a given function. Recall from your previous math classes that the slope formula is the change in y over the change in x.
By finding the change between two variables in a given interval, we can obtain the slope of the secant line of a function, which helps us understand the rate of change between two points in a given function. As you use different points to measure the rate of change in a function, you will see that the secant line changes constantly by having a different slope at different intervals, as demonstrated in the series of tangent lines in the image below:

Courtesy of Calculus: Early Transcendentals by Larson and Edwards.
This image displays several secant lines of the same function. Notice how each of the secant lines has a distinct slope, which is the result of using different endpoints in the interval for measuring the rate of change.
Concept of Limits
So what are limits? Limits are going to be the focus of the first unit in this class.
Limits are expressions used to measure the rate of change at a given point. This is called the instantaneous rate of change, as it aims to find change at one particular point (for example, point a). Below is how a limit would be written and expressed mathematically:
It is important to note that due to the nature of the rate of change formula, the endpoints of the interval cannot be the same as they would result in a change of y over 0, which is undefined. In future lessons, you will use the definition of a limit to find the derivative, which is also known as the slope of the tangent line.
So…to answer the question, “can change occur at an instant?”, yes it can! Let’s get into limits further and define them.

© 2025 Fiveable Inc. All rights reserved.