Browse By Unit
1.14 Connecting Infinite Limits and Vertical Asymptotes
4 min read•june 18, 2024
1.14 Connecting Infinite Limits and Vertical Asymptotes
In topic 1.10, we explored different types of discontinuities. Today, we’ll be zooming into one specific type: discontinuities due to vertical asymptotes. 🔬
It’s extremely important to have a solid understanding of limits and be comfortable evaluating them before tackling this lesson. Make sure to brush up on the following topics first if necessary:
- 1.2: Defining Limits and Using Limit Notation
- 1.5: Determining Limits Using Algebraic Properties of Limits
- 1.6: Determining Limits Using Algebraic Manipulation
Discontinuities
Discontinuities are points where a function is undefined or exhibits a sudden change in behavior. In calculus, many theorems can only be used when functions are continuous—that’s why it’s crucial for us to know how to identify discontinuities!
Vertical Asymptotes
As you may recall from Algebra II, vertical asymptotes are vertical lines that a function approaches but never crosses. Just remember that vertical asymptotes are off-limits. Get it?! 🙃
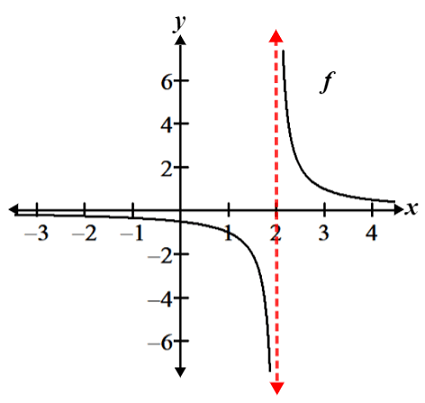
Image Courtesy of Math.net
Puns aside, knowing if a function has asymptotic behavior and where these asymptotes lie is really neat. It allows us to better visualize the functions accurately. Plus, vertical asymptotes are a type of discontinuity because they represent an x-value where a function’s behavior is unbounded.
What does this mean? As a function gets really close to this x-value, its y-value rapidly increases and approaches infinity, giving the vertical-looking part of the graph. This sudden behavior is super different from a function’s smooth, continuous behavior at most other points. Since functions can’t touch vertical asymptotes, the function can’t be evaluated at that exact x-value, making it a discontinuity.
♾️ Infinite Limits
Limits that evaluate positive or negative infinity are infinite limits. A function increases without a bound for positive infinity and decreases without a bound for negative infinity.
Connecting Infinite Limits to Vertical Asymptotes
In other words, the above notation is saying “if a function f approaches infinity as x approaches a value a”. If any of the above conditions are satisfied, we can say that there is a vertical asymptote at x = a. The function could approach infinity from the left (-), right (+), or both sides.
Infinite Limits and Vertical Asymptotes Practice
Limits and Vertical Asymptotes: Example 1
❓Using limits, show that x = -3 is a vertical asymptote for .
Solution to Example 1
If x = -3 is a vertical asymptote, then the limit as x approaches -3 must evaluate to either positive or negative infinity.
Let’s try
If you substitute -3 for x, the denominator becomes 0. The limit evaluates to positive infinity because 1 is being divided by 0. We know the function approaches positive infinity and not negative infinity because we are approaching x = -3 from the right (+) side. x is extremely close to -3 (think -2.99999…), but -3 is still more negative than that. Thus, while the denominator is approaching 0, the function grows upwards positively.
Similarly, try .
The same logic applies where the limit evaluates to infinity because 1 is divided by 0. This time, the function is approaching negative infinity because we are approaching x = -3 from the left (-) side. x is extremely close to -3 but is ever so slightly more negative than -3 (think something like -3.00000001). Thus, while the denominator is approaching 0, the function is negative and grows downwards unbounded.
Limits and Vertical Asymptotes: Example 2
Find the vertical asymptote for the function .
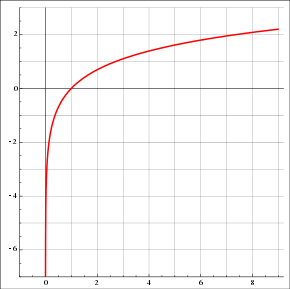
Image Courtesy of Wikipedia.
Solution to Example 2
Knowing the general shape of the natural log graph, we can determine that there is a vertical asymptote at x = 0. Let’s prove this with an infinite limit!
ln(0) does not exist because there is no n that would make equal to 0. We know that the limit evaluates to negative infinity because as x gets smaller and approaches 0 from the right (+) side, ln(x) becomes more and more negative. Remember that e is approximately 2.718, so for to be close to 0, n must be negative.
<< Hide Menu
1.14 Connecting Infinite Limits and Vertical Asymptotes
4 min read•june 18, 2024
1.14 Connecting Infinite Limits and Vertical Asymptotes
In topic 1.10, we explored different types of discontinuities. Today, we’ll be zooming into one specific type: discontinuities due to vertical asymptotes. 🔬
It’s extremely important to have a solid understanding of limits and be comfortable evaluating them before tackling this lesson. Make sure to brush up on the following topics first if necessary:
- 1.2: Defining Limits and Using Limit Notation
- 1.5: Determining Limits Using Algebraic Properties of Limits
- 1.6: Determining Limits Using Algebraic Manipulation
Discontinuities
Discontinuities are points where a function is undefined or exhibits a sudden change in behavior. In calculus, many theorems can only be used when functions are continuous—that’s why it’s crucial for us to know how to identify discontinuities!
Vertical Asymptotes
As you may recall from Algebra II, vertical asymptotes are vertical lines that a function approaches but never crosses. Just remember that vertical asymptotes are off-limits. Get it?! 🙃

Image Courtesy of Math.net
Puns aside, knowing if a function has asymptotic behavior and where these asymptotes lie is really neat. It allows us to better visualize the functions accurately. Plus, vertical asymptotes are a type of discontinuity because they represent an x-value where a function’s behavior is unbounded.
What does this mean? As a function gets really close to this x-value, its y-value rapidly increases and approaches infinity, giving the vertical-looking part of the graph. This sudden behavior is super different from a function’s smooth, continuous behavior at most other points. Since functions can’t touch vertical asymptotes, the function can’t be evaluated at that exact x-value, making it a discontinuity.
♾️ Infinite Limits
Limits that evaluate positive or negative infinity are infinite limits. A function increases without a bound for positive infinity and decreases without a bound for negative infinity.
Connecting Infinite Limits to Vertical Asymptotes
In other words, the above notation is saying “if a function f approaches infinity as x approaches a value a”. If any of the above conditions are satisfied, we can say that there is a vertical asymptote at x = a. The function could approach infinity from the left (-), right (+), or both sides.
Infinite Limits and Vertical Asymptotes Practice
Limits and Vertical Asymptotes: Example 1
❓Using limits, show that x = -3 is a vertical asymptote for .
Solution to Example 1
If x = -3 is a vertical asymptote, then the limit as x approaches -3 must evaluate to either positive or negative infinity.
Let’s try
If you substitute -3 for x, the denominator becomes 0. The limit evaluates to positive infinity because 1 is being divided by 0. We know the function approaches positive infinity and not negative infinity because we are approaching x = -3 from the right (+) side. x is extremely close to -3 (think -2.99999…), but -3 is still more negative than that. Thus, while the denominator is approaching 0, the function grows upwards positively.
Similarly, try .
The same logic applies where the limit evaluates to infinity because 1 is divided by 0. This time, the function is approaching negative infinity because we are approaching x = -3 from the left (-) side. x is extremely close to -3 but is ever so slightly more negative than -3 (think something like -3.00000001). Thus, while the denominator is approaching 0, the function is negative and grows downwards unbounded.
Limits and Vertical Asymptotes: Example 2
Find the vertical asymptote for the function .

Image Courtesy of Wikipedia.
Solution to Example 2
Knowing the general shape of the natural log graph, we can determine that there is a vertical asymptote at x = 0. Let’s prove this with an infinite limit!
ln(0) does not exist because there is no n that would make equal to 0. We know that the limit evaluates to negative infinity because as x gets smaller and approaches 0 from the right (+) side, ln(x) becomes more and more negative. Remember that e is approximately 2.718, so for to be close to 0, n must be negative.

© 2025 Fiveable Inc. All rights reserved.