Browse By Unit
1.7 Selecting Procedures for Determining Limits
7 min read•june 18, 2024
1.7 Selecting Procedures for Determining Limits
Welcome to Selecting Procedures for Determining Limits! In this guide, we’re going to be covering how to select a procedure for determining the limit of an equation. The previous topics covered in Unit 1 have described the different methods for determining the limit of an equation. Now it is up to you to figure out which method to use under which circumstance. You got this! 🍀
Let’s Recap: Determining Limits
For basic information regarding limits, you can look at an overview of limits in this Unit One Overview: Limits & Continuity. Let’s review the previously-discussed methods on how to determine limits:
♾️ Determining Limits From A Graph
We can determine the limit if given a graph. If the y-value is approaching a certain value as the x-value approaches infinity, then we have found our limit. If the x-value approaches a certain y-value from the left and right, then that y-value is our limit.
To review a bit more of this topic, check out key topic 1.3: Estimating Limit Values from Graphs.
🕵️♂️ Evaluating Limits Graphically: Practice Time!
Take the graph of y =
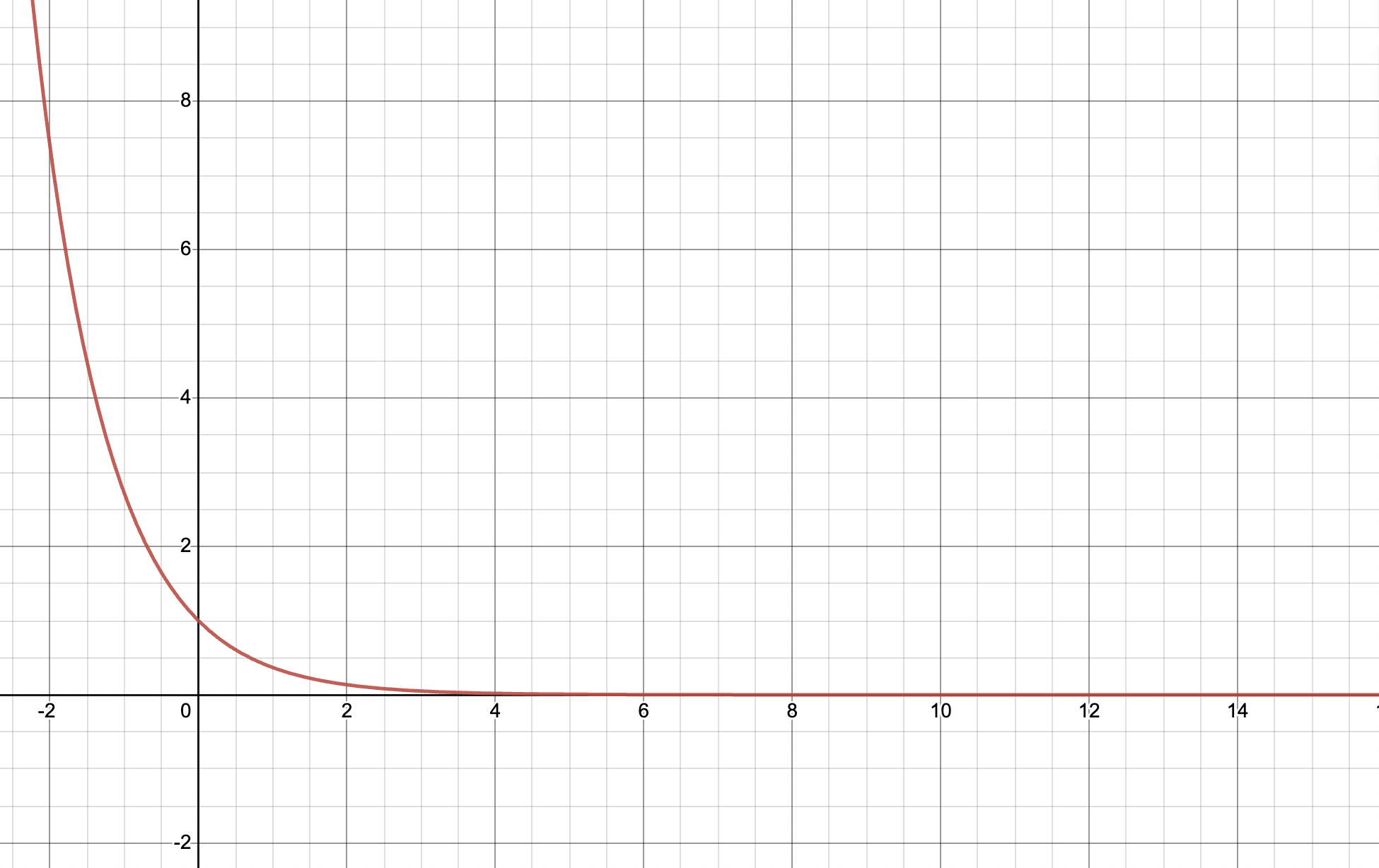
Image Courtesy of Desmos
What is the limit of this graph? When approaching this question, think of it as, “What does y approach as x approaches infinity?”
From the graph, we can see that as x approaches infinity, y approaches 0. Therefore, the limit of y = is 0. For more practice, be sure to check out key topic 1.3.
🔢 Estimating Limit Values From Tables
When given a table in a problem, we can conclude what value y is approaching by looking at patterns within the tables. If the y-value is increasing up to a certain value or decreasing up to a certain value, we can conclude that the limit of the function presented in the table is that value.
To review this content, check out key topic 1.4: Estimating Limit Values from Tables.
🕵️♂️ Evaluating Limits Numerically: Test your knowledge!

Image Courtesy of Coping With Calculus
What is the limit as the function approaches 0?
Do you have your answer yet? Well, let’s go over it!
We are given the x and y values of a certain function. From this, we can see that the function approaches a certain value at 0. Given that the function when x=-0.001 has a y-value of 1.9995, and when the function has an x-value of 0.001, the y-value is 2.0005, we can reasonably estimate that the y-value will be 2 when x is 0. Therefore, the value that the function approaches at 0, or the limit of the function, is 0.
Some more examples can be found here! 😎
✏️ Determining Limits Using Algebraic Properties
Let’s review some basic rules from key topic 1.5:
- ➕ The limit of a sum of functions is equal to the limit of each individual equation added together.
- ➖ The limit of a difference of functions is equal to the limit of one of the functions subtracted by the other.
- ✖️ The limit of a product of functions is equal to the limit of each individual equation multiplied together.
- ➗ The limit of a quotient of functions is equal to the limit of one equation divided by the limit of the other equation.
What is a composite function?

Image courtesy of OnLine Math Learning
To find the limit of composite functions given the function f(g(x)), where g(x) is the inner function and f(x) is the outer function:
- Find the limit of g(x). We’ll call this value ‘z’.
- Plug ‘z’ into f(g(x)) for (g(x)), so you are evaluating f(z).
- F(z) is your limit of the composite function!
🕵️♂️ Evaluating Limits Algebraically: Practice Problem Time!
Consider the composite function , where , and . Find the limit for this function as x approaches 3.
Try it on your own first…
Are you ready for a solution? Let’s do it! 😌
- Find the limit of g(x) as x approaches 3. We can do this by simply plugging 3 in for x. The limit for g(x) as x approaches 3 is or .
- Plug this value into your f(x) equation! f(x) = + 5. That is your solution! 🥳
🖊️ Determining Limits Using Algebraic Manipulation
Using this method to determine the limit of an equation is essentially all about manipulating the equation to get it to a form where we can easily plug in a value and get the limit of the equation. To do this, you can:
- Multiply by conjugates to simplify functions with radicals
- Use L’Hopitals to manipulate the equation into a solvable form
- Using mathematical techniques to simplify rational functions
To review each of these in-depth and do some practice, check out key topic 1.6: Determining Limits Using Algebraic Manipulation.
What is the Squeeze Theorem?
We will also cover the Squeeze Theorem under this method. So what is the squeeze theorem?
We have three functions f(x), g(x), and h(x), and . If a is a constant, and the limit as x → a for f(x) = L, and the limit as x → a for h(x) = L, then the limit as x → a for g(x) = L.
Don’t worry, the next key topic goes more in-depth about the Squeeze Theorem.
🕵️♂️ Evaluating Limits Algebraically: Practice Problem
The following question is from GeeksforGeeks. All credit to GeeksforGeeks.
Given the equation, , find the limit as x → 3.
Try it on your own first….
Now let’s get started! We want to start by simplifying the numerator. So we multiply the numerator and denominator of the fraction by the conjugate of the numerator! Follow these steps:
Now plug in 3 for x. By doing this, you’ll know that is your answer!
Now that we’ve reviewed all the methods thus far for solving for the limit of an equation, let’s move to the main purpose of this guide: determining which method you should use to solve for the limit.
🪧Selecting Procedures for Determining Limits
〽️ Procedure 1: Visual Representation
If a problem gives you a graph and asks you to find the limit of the function at a certain x-value, then you should use visual representation to scan for what the limit is, to scan for what y-value the graph approaches as your x-value approaches infinity. This should give you a good estimation of what the limit of the graph is.
🔢Procedure 2: Tables
If a problem gives you a table depicting the x and y values of a function, then you should use the tables method we discussed above to estimate the value of the limit of the function. Based on the x-values, we can see the y-values approaching a certain point or following a certain pattern.
Remember, the limit is just what value the function approaches at a given point. Scan for patterns among the y-values of the function in the table to determine your limit at the given x value!
🤔 Procedure 3: Algebraic Properties
Some questions may be straightforward. If a problem gives you two functions and asks you to find the limit of the sum of the functions, we know that this is testing our knowledge of limit theorems. All we need to do is find the limit of the two functions separately and add them together to get our answer.
If any question asks you to find the limit of an equation in the form f(g(x)), we know that we’re dealing with a composite function, and we should follow the appropriate steps as necessary to solve that.
💡Procedure 4: Algebraic Manipulation
You may be asked to find the limit of more complex functions. If you see an equation of the form , where x is your variable, and a and b are both constants, you know that you will likely have to multiply the numerator and denominator by the conjugate of in order to change the equation into a more easily solvable form.
🗒️ Determining Limits: Practice
You guessed it…it’s practice problem time!
Given the equation , find the limit as x → .
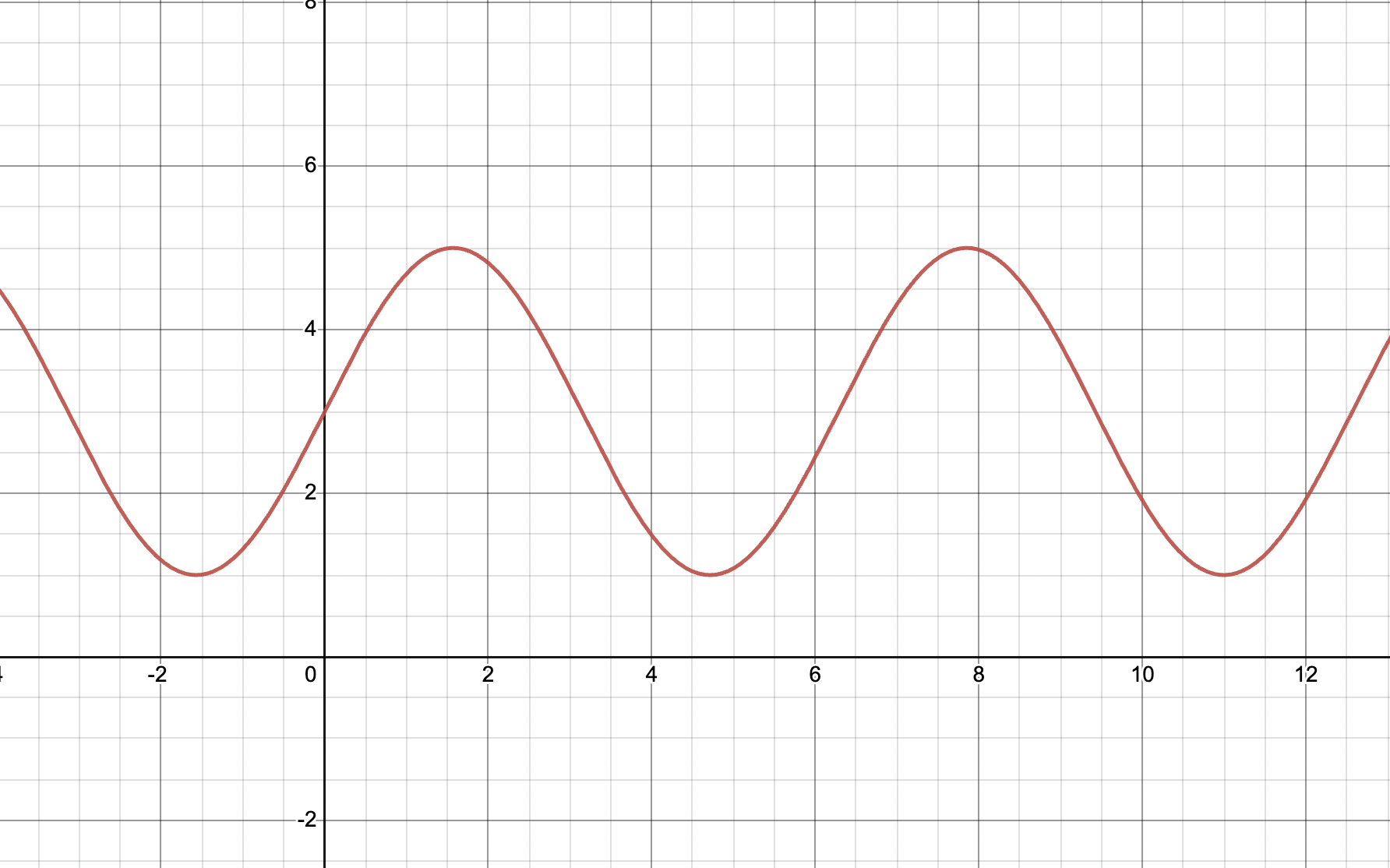
Image created with Desmos.
Which technique should be used to solve for this limit, if you are given the graph for a problem?
Answer: Visual Representation. For any question that gives you the graph of the equation, you should try visual representation as your first tactic to estimate the limit.
What is the limit of y = 2sin(x) + 3?
Answer: Based on the graph, we can conclude that the function approaches 5 as x —> .
You got this! 🍀
<< Hide Menu
1.7 Selecting Procedures for Determining Limits
7 min read•june 18, 2024
1.7 Selecting Procedures for Determining Limits
Welcome to Selecting Procedures for Determining Limits! In this guide, we’re going to be covering how to select a procedure for determining the limit of an equation. The previous topics covered in Unit 1 have described the different methods for determining the limit of an equation. Now it is up to you to figure out which method to use under which circumstance. You got this! 🍀
Let’s Recap: Determining Limits
For basic information regarding limits, you can look at an overview of limits in this Unit One Overview: Limits & Continuity. Let’s review the previously-discussed methods on how to determine limits:
♾️ Determining Limits From A Graph
We can determine the limit if given a graph. If the y-value is approaching a certain value as the x-value approaches infinity, then we have found our limit. If the x-value approaches a certain y-value from the left and right, then that y-value is our limit.
To review a bit more of this topic, check out key topic 1.3: Estimating Limit Values from Graphs.
🕵️♂️ Evaluating Limits Graphically: Practice Time!
Take the graph of y =

Image Courtesy of Desmos
What is the limit of this graph? When approaching this question, think of it as, “What does y approach as x approaches infinity?”
From the graph, we can see that as x approaches infinity, y approaches 0. Therefore, the limit of y = is 0. For more practice, be sure to check out key topic 1.3.
🔢 Estimating Limit Values From Tables
When given a table in a problem, we can conclude what value y is approaching by looking at patterns within the tables. If the y-value is increasing up to a certain value or decreasing up to a certain value, we can conclude that the limit of the function presented in the table is that value.
To review this content, check out key topic 1.4: Estimating Limit Values from Tables.
🕵️♂️ Evaluating Limits Numerically: Test your knowledge!

Image Courtesy of Coping With Calculus
What is the limit as the function approaches 0?
Do you have your answer yet? Well, let’s go over it!
We are given the x and y values of a certain function. From this, we can see that the function approaches a certain value at 0. Given that the function when x=-0.001 has a y-value of 1.9995, and when the function has an x-value of 0.001, the y-value is 2.0005, we can reasonably estimate that the y-value will be 2 when x is 0. Therefore, the value that the function approaches at 0, or the limit of the function, is 0.
Some more examples can be found here! 😎
✏️ Determining Limits Using Algebraic Properties
Let’s review some basic rules from key topic 1.5:
- ➕ The limit of a sum of functions is equal to the limit of each individual equation added together.
- ➖ The limit of a difference of functions is equal to the limit of one of the functions subtracted by the other.
- ✖️ The limit of a product of functions is equal to the limit of each individual equation multiplied together.
- ➗ The limit of a quotient of functions is equal to the limit of one equation divided by the limit of the other equation.
What is a composite function?

Image courtesy of OnLine Math Learning
To find the limit of composite functions given the function f(g(x)), where g(x) is the inner function and f(x) is the outer function:
- Find the limit of g(x). We’ll call this value ‘z’.
- Plug ‘z’ into f(g(x)) for (g(x)), so you are evaluating f(z).
- F(z) is your limit of the composite function!
🕵️♂️ Evaluating Limits Algebraically: Practice Problem Time!
Consider the composite function , where , and . Find the limit for this function as x approaches 3.
Try it on your own first…
Are you ready for a solution? Let’s do it! 😌
- Find the limit of g(x) as x approaches 3. We can do this by simply plugging 3 in for x. The limit for g(x) as x approaches 3 is or .
- Plug this value into your f(x) equation! f(x) = + 5. That is your solution! 🥳
🖊️ Determining Limits Using Algebraic Manipulation
Using this method to determine the limit of an equation is essentially all about manipulating the equation to get it to a form where we can easily plug in a value and get the limit of the equation. To do this, you can:
- Multiply by conjugates to simplify functions with radicals
- Use L’Hopitals to manipulate the equation into a solvable form
- Using mathematical techniques to simplify rational functions
To review each of these in-depth and do some practice, check out key topic 1.6: Determining Limits Using Algebraic Manipulation.
What is the Squeeze Theorem?
We will also cover the Squeeze Theorem under this method. So what is the squeeze theorem?
We have three functions f(x), g(x), and h(x), and . If a is a constant, and the limit as x → a for f(x) = L, and the limit as x → a for h(x) = L, then the limit as x → a for g(x) = L.
Don’t worry, the next key topic goes more in-depth about the Squeeze Theorem.
🕵️♂️ Evaluating Limits Algebraically: Practice Problem
The following question is from GeeksforGeeks. All credit to GeeksforGeeks.
Given the equation, , find the limit as x → 3.
Try it on your own first….
Now let’s get started! We want to start by simplifying the numerator. So we multiply the numerator and denominator of the fraction by the conjugate of the numerator! Follow these steps:
Now plug in 3 for x. By doing this, you’ll know that is your answer!
Now that we’ve reviewed all the methods thus far for solving for the limit of an equation, let’s move to the main purpose of this guide: determining which method you should use to solve for the limit.
🪧Selecting Procedures for Determining Limits
〽️ Procedure 1: Visual Representation
If a problem gives you a graph and asks you to find the limit of the function at a certain x-value, then you should use visual representation to scan for what the limit is, to scan for what y-value the graph approaches as your x-value approaches infinity. This should give you a good estimation of what the limit of the graph is.
🔢Procedure 2: Tables
If a problem gives you a table depicting the x and y values of a function, then you should use the tables method we discussed above to estimate the value of the limit of the function. Based on the x-values, we can see the y-values approaching a certain point or following a certain pattern.
Remember, the limit is just what value the function approaches at a given point. Scan for patterns among the y-values of the function in the table to determine your limit at the given x value!
🤔 Procedure 3: Algebraic Properties
Some questions may be straightforward. If a problem gives you two functions and asks you to find the limit of the sum of the functions, we know that this is testing our knowledge of limit theorems. All we need to do is find the limit of the two functions separately and add them together to get our answer.
If any question asks you to find the limit of an equation in the form f(g(x)), we know that we’re dealing with a composite function, and we should follow the appropriate steps as necessary to solve that.
💡Procedure 4: Algebraic Manipulation
You may be asked to find the limit of more complex functions. If you see an equation of the form , where x is your variable, and a and b are both constants, you know that you will likely have to multiply the numerator and denominator by the conjugate of in order to change the equation into a more easily solvable form.
🗒️ Determining Limits: Practice
You guessed it…it’s practice problem time!
Given the equation , find the limit as x → .

Image created with Desmos.
Which technique should be used to solve for this limit, if you are given the graph for a problem?
Answer: Visual Representation. For any question that gives you the graph of the equation, you should try visual representation as your first tactic to estimate the limit.
What is the limit of y = 2sin(x) + 3?
Answer: Based on the graph, we can conclude that the function approaches 5 as x —> .
You got this! 🍀

© 2025 Fiveable Inc. All rights reserved.