Browse By Unit
10.12 Lagrange Error Bound
At this point in your Calculus journey, you should have learned what exactly a Maclaurin and Taylor polynomial is, how to write one, and how to use them to approximate non-algebraic functions. If you’ve ever wondered just how good these approximations are, and by what value this approximation is wrong by, this lesson is for you.
This guide will discuss the Lagrange Error Bound and how this can be used to determine the largest, or maximum, number of error your Taylor polynomial is.
🟥Review: Taylor Polynomials
In case you’re not familiar with them, or would like to gain further proficiency in writing them, we will touch up on our knowledge of Taylor Polynomials. To generalize what they are, Taylor polynomials are approximations of functions using polynomial expressions by finding derivatives. All Taylor series are centered at a certain point, which is what’s used to estimate the functions behavior. Here’s the general formula for the Taylor Polynomial:
There are some series that are frequently asked about on the AP exam which are helpful to have memorized, but nonetheless all Taylor series can be derived by taking the derivative of the function centered at wherever you’re given. Here are some common series centered at 0:
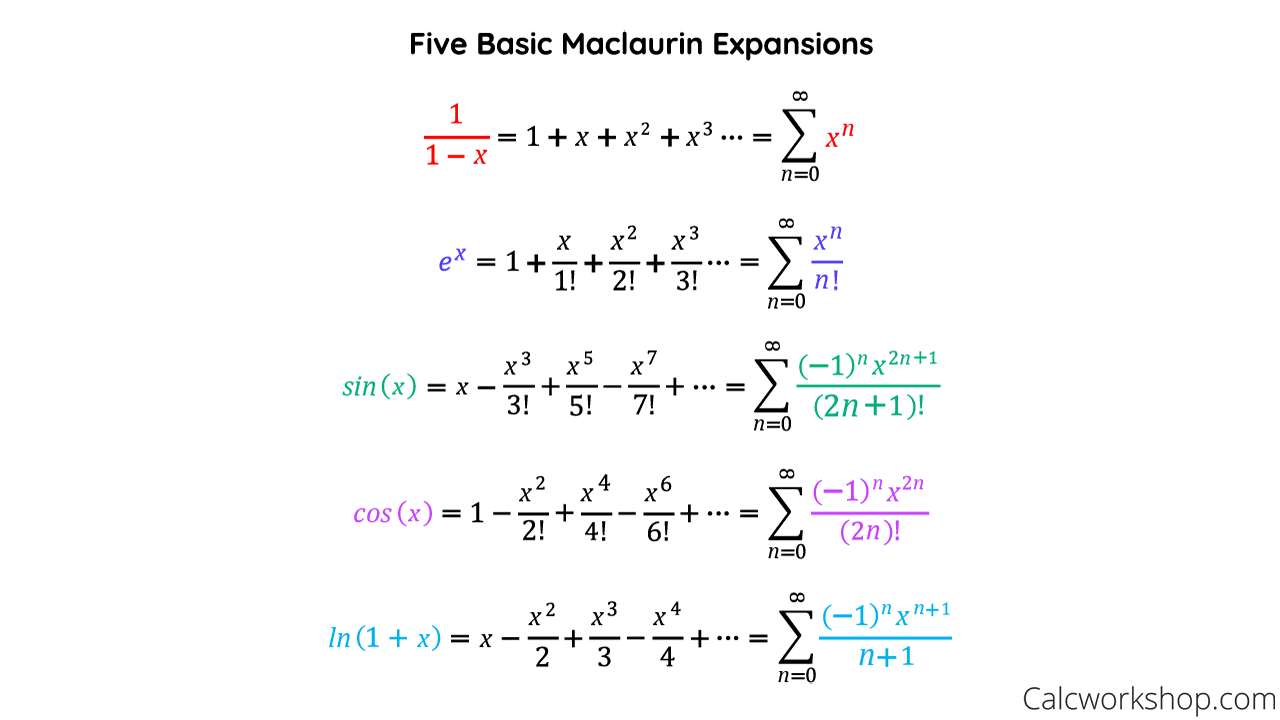
Image Courtesy of Calcworkshop
To further review Taylor polynomials, check out 10.11 Finding Taylor Polynomial Approximations of Functions.
🔷 Lagrange Error Bound
Another way to look at the definition of the Taylor polynomial is to see it as being an approximation. Knowing this, you can determine that your approximation plus an unknown remainder will equal your original function:
If we rewrote the right side of the equation in accordance to Taylor’s theorem, you can get a clearer image on what exactly is:
In simple terms, the remainder of a Taylor polynomial is the term following the degree of the polynomial, or “n+1”. So, when calculating your error bound, simply calculate the next term in the sequence.
Example 1: Lagrange Error Bound
Using the Maclaurin polynomial of to the 3rd degree to approximate , what is the Lagrange Error bound?
To begin answering this problem, we must first write out the 3rd degree Maclaurin polynomial of
Plugging in -1 for x, we get:
Now, lets find our error bound (the remainder):
To find what exactly is, we must determine what number in the interval [-1,0] will give us the maximum number of error. Since the 4th derivative of is , the largest possible number is 1. So, we can say that our .
Awesome work! 🤗
⭐Practice AP FRQ 2008 #3
The following free-response question (FRQ) is Question 3 from the 2008 AP Calculus BC examination administered by College Board. All credit to College Board.
Let h be a function having derivatives of all orders for . Selected values of h and its first four derivatives are indicated in the table above. The function h and these four derivatives are increasing on the interval .
b) Write the third-degree Taylor polynomial for h about x=2 and use it to approximate h(1.9).
Using the table given, you can construct the polynomial by using the general formula for any Taylor series:
c) Use the Lagrange error bound to show that the third-degree Taylor polynomial for h about x=2 approximates h(1.9) with error less than 3 x .
Using the given on the interval , we can find our remainder to be:
🚀Closing
Great job! You have just learned to calculate the Lagrange Error Bound of Maclaurin and Taylor polynomials. This is a frequently asked question on FRQs for the BC exam, so make sure to practice what you’ve just learned. 🎉
<< Hide Menu
10.12 Lagrange Error Bound
At this point in your Calculus journey, you should have learned what exactly a Maclaurin and Taylor polynomial is, how to write one, and how to use them to approximate non-algebraic functions. If you’ve ever wondered just how good these approximations are, and by what value this approximation is wrong by, this lesson is for you.
This guide will discuss the Lagrange Error Bound and how this can be used to determine the largest, or maximum, number of error your Taylor polynomial is.
🟥Review: Taylor Polynomials
In case you’re not familiar with them, or would like to gain further proficiency in writing them, we will touch up on our knowledge of Taylor Polynomials. To generalize what they are, Taylor polynomials are approximations of functions using polynomial expressions by finding derivatives. All Taylor series are centered at a certain point, which is what’s used to estimate the functions behavior. Here’s the general formula for the Taylor Polynomial:
There are some series that are frequently asked about on the AP exam which are helpful to have memorized, but nonetheless all Taylor series can be derived by taking the derivative of the function centered at wherever you’re given. Here are some common series centered at 0:

Image Courtesy of Calcworkshop
To further review Taylor polynomials, check out 10.11 Finding Taylor Polynomial Approximations of Functions.
🔷 Lagrange Error Bound
Another way to look at the definition of the Taylor polynomial is to see it as being an approximation. Knowing this, you can determine that your approximation plus an unknown remainder will equal your original function:
If we rewrote the right side of the equation in accordance to Taylor’s theorem, you can get a clearer image on what exactly is:
In simple terms, the remainder of a Taylor polynomial is the term following the degree of the polynomial, or “n+1”. So, when calculating your error bound, simply calculate the next term in the sequence.
Example 1: Lagrange Error Bound
Using the Maclaurin polynomial of to the 3rd degree to approximate , what is the Lagrange Error bound?
To begin answering this problem, we must first write out the 3rd degree Maclaurin polynomial of
Plugging in -1 for x, we get:
Now, lets find our error bound (the remainder):
To find what exactly is, we must determine what number in the interval [-1,0] will give us the maximum number of error. Since the 4th derivative of is , the largest possible number is 1. So, we can say that our .
Awesome work! 🤗
⭐Practice AP FRQ 2008 #3
The following free-response question (FRQ) is Question 3 from the 2008 AP Calculus BC examination administered by College Board. All credit to College Board.
Let h be a function having derivatives of all orders for . Selected values of h and its first four derivatives are indicated in the table above. The function h and these four derivatives are increasing on the interval .
b) Write the third-degree Taylor polynomial for h about x=2 and use it to approximate h(1.9).
Using the table given, you can construct the polynomial by using the general formula for any Taylor series:
c) Use the Lagrange error bound to show that the third-degree Taylor polynomial for h about x=2 approximates h(1.9) with error less than 3 x .
Using the given on the interval , we can find our remainder to be:
🚀Closing
Great job! You have just learned to calculate the Lagrange Error Bound of Maclaurin and Taylor polynomials. This is a frequently asked question on FRQs for the BC exam, so make sure to practice what you’ve just learned. 🎉

© 2025 Fiveable Inc. All rights reserved.