Browse By Unit
10.3 The nth Term Test for Divergence
Welcome back to Unit 10 of AP Calculus BC! Today, we’re going to discuss the nth-term test for divergence with series. Let’s get started!
🤷♀️ What is the nth Term Test for Divergence?
As the name suggests the nth Divergence test tells us if a series will diverge! (mind-blowing stuff guys, I know 🤯). The Divergence test states that:
As we can see, if the nth term doesn't approach 0, the series diverges. On the other hand, if the nth term approaches 0, it creates a situation where the series might converge or still diverge. The crucial point here is that the fate of the series hinges on whether the nth term tends towards zero or not.
🤓 Divergence Test Walkthrough
Let’s try a practice problem together! There are really only 3 steps involved with this:
- ✏️ Convert to limit notation.
- 📏 Evaluate the limit.
- 🤔 Make your conclusion based on the nth-term test.
Determine if the series diverges.
✏️ Step 1: Convert to limit notation.
📏 Step 2: Evaluate the limit.
Recall that any number divided by is 0.
Not too bad, right? We’re mainly just applying a new test to the mathematics that we are already familiar with!
📝 Divergence Test Practice Problems
Try the following two practice questions yourself!
✅ Divergence Test: Solution 1
Remember the three steps involved and the nth-term test itself.
Great work!
✅ Divergence Test: Solution 2
Last question 🎉
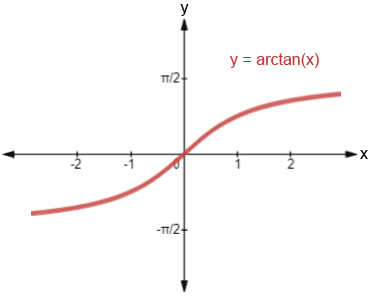
Image courtesy of Math.net
As arctan goes to , it stays at .
🕺 Closing
In conclusion, the nth Term Test for Divergence is a powerful tool for determining whether a series diverges. Remember, if the limit of the nth term does not approach zero, the series diverges. However, passing the divergence test doesn't provide information about convergence. Good luck! 🍀
<< Hide Menu
10.3 The nth Term Test for Divergence
Welcome back to Unit 10 of AP Calculus BC! Today, we’re going to discuss the nth-term test for divergence with series. Let’s get started!
🤷♀️ What is the nth Term Test for Divergence?
As the name suggests the nth Divergence test tells us if a series will diverge! (mind-blowing stuff guys, I know 🤯). The Divergence test states that:
As we can see, if the nth term doesn't approach 0, the series diverges. On the other hand, if the nth term approaches 0, it creates a situation where the series might converge or still diverge. The crucial point here is that the fate of the series hinges on whether the nth term tends towards zero or not.
🤓 Divergence Test Walkthrough
Let’s try a practice problem together! There are really only 3 steps involved with this:
- ✏️ Convert to limit notation.
- 📏 Evaluate the limit.
- 🤔 Make your conclusion based on the nth-term test.
Determine if the series diverges.
✏️ Step 1: Convert to limit notation.
📏 Step 2: Evaluate the limit.
Recall that any number divided by is 0.
Not too bad, right? We’re mainly just applying a new test to the mathematics that we are already familiar with!
📝 Divergence Test Practice Problems
Try the following two practice questions yourself!
✅ Divergence Test: Solution 1
Remember the three steps involved and the nth-term test itself.
Great work!
✅ Divergence Test: Solution 2
Last question 🎉

Image courtesy of Math.net
As arctan goes to , it stays at .
🕺 Closing
In conclusion, the nth Term Test for Divergence is a powerful tool for determining whether a series diverges. Remember, if the limit of the nth term does not approach zero, the series diverges. However, passing the divergence test doesn't provide information about convergence. Good luck! 🍀

© 2025 Fiveable Inc. All rights reserved.