Browse By Unit
2.3 Estimating Derivatives of a Function at a Point
3 min read•june 18, 2024
Sumi Vora
Sumi Vora
2.3 Estimating Derivatives of a Function at a Point
Welcome back to AP Calculus with Fiveable! This topic focuses on estimating the derivative of a function at a single point. Estimating derivatives will allow us to approximate a rate of change in an instant when we are unable to determine the derivative by hand.
We’ve just started learning about derivatives, so let's keep building our skills. 🙌
🗒️ Methods to Estimate Derivatives
A derivative represents the rate of change of a function. A derivative at a point can tell us how much a function is changing at an instant.
When we’re estimating a derivative, we are approximating at a point. This can be done by taking a small interval around the point of interest, and approximating the of the over that interval. The smaller the interval, the more accurate the estimate will be. The estimated derivative is represented by the symbol or where x or a is the point of interest.
There are several methods to estimating derivatives:
- 📝 By Hand - We can use the limit definition of a derivative, as it approximates the derivative.
- 📈 Graphically - To estimate the derivative at a point, we can draw a tangent line to the graph of the function at that point. The slope of that tangent line is an estimate of the derivative of that point.
- 💻 Using Technology - We can use a calculator or computer software, like Desmos!
More often than not, you’ll be estimating derivatives by hand and using a calculator. Let’s dive in.
📝 Estimating Derivatives by Hand
A good estimation of a derivative at a point is to calculate the slope between the point and another point close to it. Therefore, we can use this definition to approximate the derivative. This is because a derivative represents the rate of change as the distance, h, between the two points approaches 0. Review your derivative definitions here: Defining the Derivative of a Function.
Let’s use this technique with the following free-response question (FRQ), which is from the 2021 AP Calculus AB examination administered by College Board. All credit to College Board.
🧫 Bacteria Density
The density of a bacteria population in a circular petri dish at a distance centimeters from the center of the dish is given by an increasing, differentiable function , where is measured in milligrams per square centimeter.
Values of for selected values of are given in the table below.
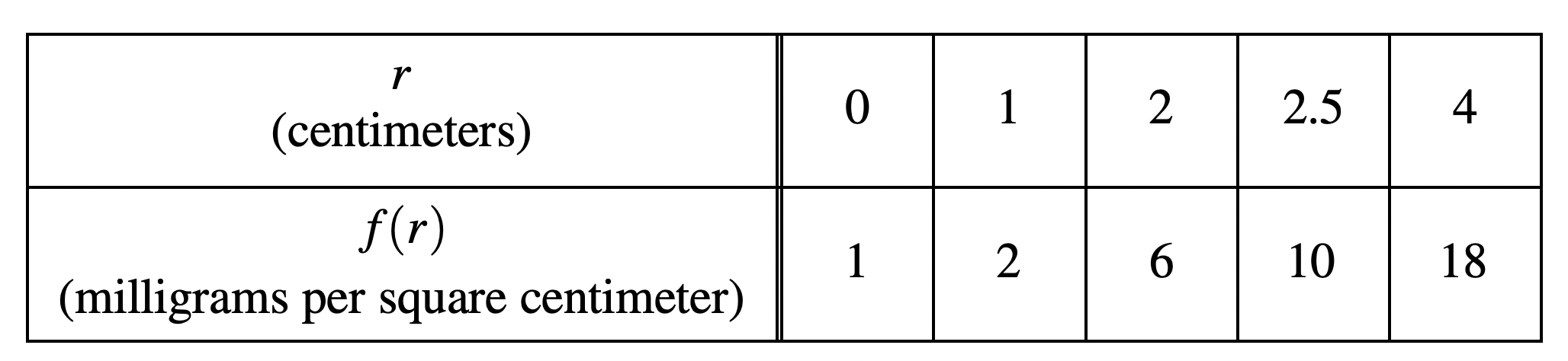
Table Courtesy of College Board. All credit to College Board.
Use the data in the table to estimate . Using correct units, interpret the meaning of your answer in the context of this problem.
a) Estimating
Remember that a derivative can be found using this definition: , where we are calculating the slope between two points close to one another.
In this case, the best points to use would be and because they are an equal distance away from the point .
Therefore, you can estimate with the following:
b) Interpreting
When you interpret data, you have to put the math into context of the question, which in this case, is the density of bacteria.
When the radius of the petri dish is 2.25 centimeters, the density of bacteria, in milligrams per square centimeter, will be increasing by 8 milligrams per square centimeter per centimeter.
The above answers would accumulate 2/2 points for this part of the FRQ! Nice work. ✅
💻 Estimating Derivatives with Technology
Technology, such as a graphing calculator, can allow us to immediately calculate the derivative of a function. If you have a graphing calculator such as a TI-Nspire, the calculator can easily find the derivative of a function at a point! Otherwise, you can use an online tool such as Desmos to estimate the derivative at a point. Let’s work through the following example with both a TI-Nspire and Desmos.
📈 Estimating Derivatives with a Calculator
Estimate the derivative of at .
Using a graphing calculator is the fastest way to calculate in this scenario.
For the TI-Nspire specifically, you can go to Menu > Calculus > Numerical Derivative at a Point. Make sure your calculator is set to radian mode!
Since the dependent variable of this function is , we must take the derivative with respect to . The value we are trying to calculate at is 2, and we are calculating only the first derivative. Then you can plug in the expression for , and your function should look similar to this:
When you press enter, the calculator will give you the value of .
So . Good job! 😁
📈 Estimating Derivatives with Desmos
Now let’s attempt this question with Desmos. First, input the function into the Desmos calculator as . Then, you can simply type and Desmos will calculate the value for you! You should get that . Looking at the graph, we can guess that should be negative, since the function is decreasing at , so we should have everything calculated correctly. You're on fire! 🔥
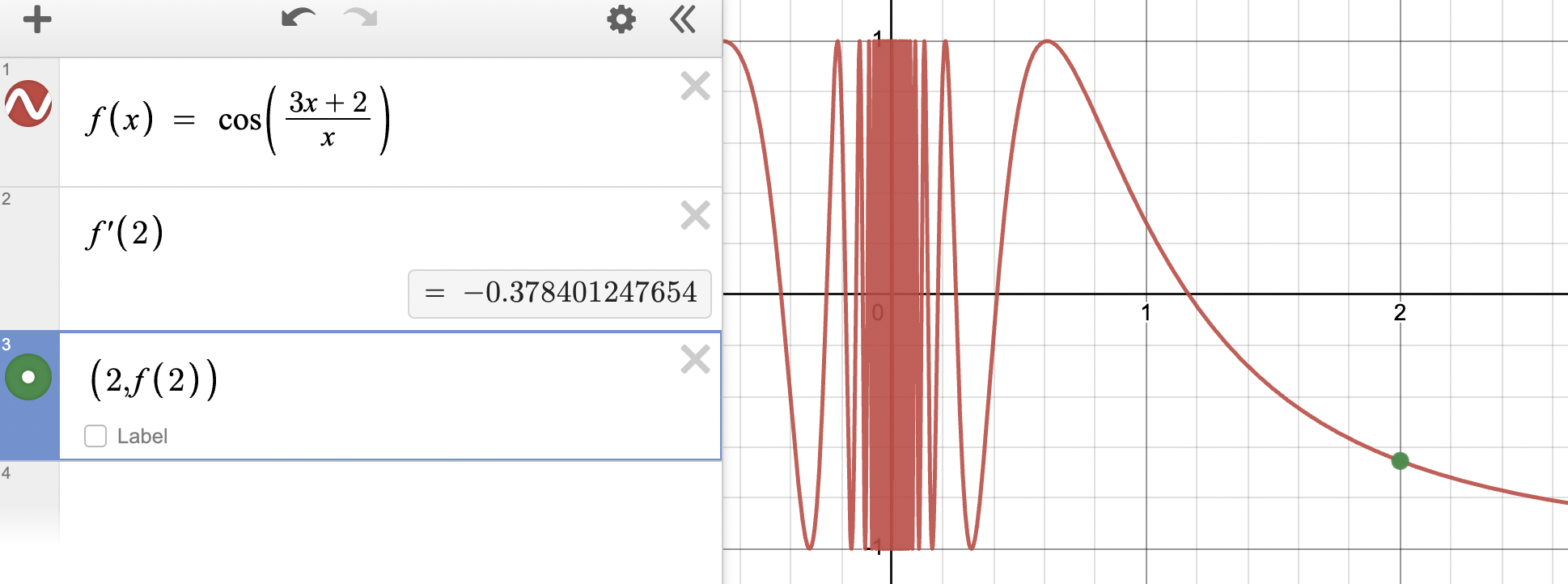
Graph created using Desmos
🌟 Closing
Nice work! Estimating derivatives is a key foundational topic for AP Calculus. You can anticipate encountering a few questions requiring you to estimate derivatives on the exam, both in multiple-choice and as part of a free response.

Image Courtesy of Giphy
<< Hide Menu
2.3 Estimating Derivatives of a Function at a Point
3 min read•june 18, 2024
Sumi Vora
Sumi Vora
2.3 Estimating Derivatives of a Function at a Point
Welcome back to AP Calculus with Fiveable! This topic focuses on estimating the derivative of a function at a single point. Estimating derivatives will allow us to approximate a rate of change in an instant when we are unable to determine the derivative by hand.
We’ve just started learning about derivatives, so let's keep building our skills. 🙌
🗒️ Methods to Estimate Derivatives
A derivative represents the rate of change of a function. A derivative at a point can tell us how much a function is changing at an instant.
When we’re estimating a derivative, we are approximating at a point. This can be done by taking a small interval around the point of interest, and approximating the of the over that interval. The smaller the interval, the more accurate the estimate will be. The estimated derivative is represented by the symbol or where x or a is the point of interest.
There are several methods to estimating derivatives:
- 📝 By Hand - We can use the limit definition of a derivative, as it approximates the derivative.
- 📈 Graphically - To estimate the derivative at a point, we can draw a tangent line to the graph of the function at that point. The slope of that tangent line is an estimate of the derivative of that point.
- 💻 Using Technology - We can use a calculator or computer software, like Desmos!
More often than not, you’ll be estimating derivatives by hand and using a calculator. Let’s dive in.
📝 Estimating Derivatives by Hand
A good estimation of a derivative at a point is to calculate the slope between the point and another point close to it. Therefore, we can use this definition to approximate the derivative. This is because a derivative represents the rate of change as the distance, h, between the two points approaches 0. Review your derivative definitions here: Defining the Derivative of a Function.
Let’s use this technique with the following free-response question (FRQ), which is from the 2021 AP Calculus AB examination administered by College Board. All credit to College Board.
🧫 Bacteria Density
The density of a bacteria population in a circular petri dish at a distance centimeters from the center of the dish is given by an increasing, differentiable function , where is measured in milligrams per square centimeter.
Values of for selected values of are given in the table below.

Table Courtesy of College Board. All credit to College Board.
Use the data in the table to estimate . Using correct units, interpret the meaning of your answer in the context of this problem.
a) Estimating
Remember that a derivative can be found using this definition: , where we are calculating the slope between two points close to one another.
In this case, the best points to use would be and because they are an equal distance away from the point .
Therefore, you can estimate with the following:
b) Interpreting
When you interpret data, you have to put the math into context of the question, which in this case, is the density of bacteria.
When the radius of the petri dish is 2.25 centimeters, the density of bacteria, in milligrams per square centimeter, will be increasing by 8 milligrams per square centimeter per centimeter.
The above answers would accumulate 2/2 points for this part of the FRQ! Nice work. ✅
💻 Estimating Derivatives with Technology
Technology, such as a graphing calculator, can allow us to immediately calculate the derivative of a function. If you have a graphing calculator such as a TI-Nspire, the calculator can easily find the derivative of a function at a point! Otherwise, you can use an online tool such as Desmos to estimate the derivative at a point. Let’s work through the following example with both a TI-Nspire and Desmos.
📈 Estimating Derivatives with a Calculator
Estimate the derivative of at .
Using a graphing calculator is the fastest way to calculate in this scenario.
For the TI-Nspire specifically, you can go to Menu > Calculus > Numerical Derivative at a Point. Make sure your calculator is set to radian mode!
Since the dependent variable of this function is , we must take the derivative with respect to . The value we are trying to calculate at is 2, and we are calculating only the first derivative. Then you can plug in the expression for , and your function should look similar to this:
When you press enter, the calculator will give you the value of .
So . Good job! 😁
📈 Estimating Derivatives with Desmos
Now let’s attempt this question with Desmos. First, input the function into the Desmos calculator as . Then, you can simply type and Desmos will calculate the value for you! You should get that . Looking at the graph, we can guess that should be negative, since the function is decreasing at , so we should have everything calculated correctly. You're on fire! 🔥

Graph created using Desmos
🌟 Closing
Nice work! Estimating derivatives is a key foundational topic for AP Calculus. You can anticipate encountering a few questions requiring you to estimate derivatives on the exam, both in multiple-choice and as part of a free response.

Image Courtesy of Giphy

© 2025 Fiveable Inc. All rights reserved.