Browse By Unit
4.4 Introduction to Related Rates
Using the concept of the rate of change, we can use derivatives to solve real-world problems particularly when dealing with how much something has changed in relation to another quantity. This is known as related rates in AP Calculus AB. 🧠
🤔 Using Derivative Rules
Related rates describe the process of using derivatives to calculate unknown quantities in relation to other quantities and their rates of change. Typically, problems regarding this topic are calculated concerning the quantity of time. ⏰
To solve related rate problems, several derivative rules must be applied, depending on the problem and the known and unknown quantities. This includes the chain rule, the Product Rule, and the Quotient Rule. For in-depth explanations, check out our previous study guides for explanations on these rules! They are all found in unit two, linked here.
✏️ How to Solve Related Rate Problems
Here is roughly a step-by-step process of solving related rates problems:
⛳️ Determine quantities from the problem
This includes known quantities where the amounts are explicitly mentioned in the problem and unknown quantities that are not mentioned in the problem.
📈 Model the relationship between quantities
This is done through a formula. It is important to note that if some quantities mentioned in the problem are not explicitly related to the unknown quantity that is trying to be solved, it should be replaced to simplify the formula when computing its derivatives.
👍 Apply derivative rules with respect to the unknown quantity
After coming up with a formula that encapsulates all of the quantities mentioned in the problem, use the derivative rules to derive the equation, its quantities, and their rates of change. Note that the variables in the formula must be derived WITH RESPECT to the same independent variable that is being solved (typically this is usually with respect to a variable of time .
🔢 Substitute known quantities into the derived equation & solve for the remaining quantities
Doing this will simplify the equation to the point where algebra can be applied to determine the value of unknown quantities.
This may be a lot to digest, so let’s go through a couple of examples to put this into action!
📝Related Rates Practice
Here are two practice problems you can use to get familiar with related rates.
Practice Example #1
Let’s start with an easy problem and work our way up!
To approach this problem, we can draw a picture or model of how this might look:
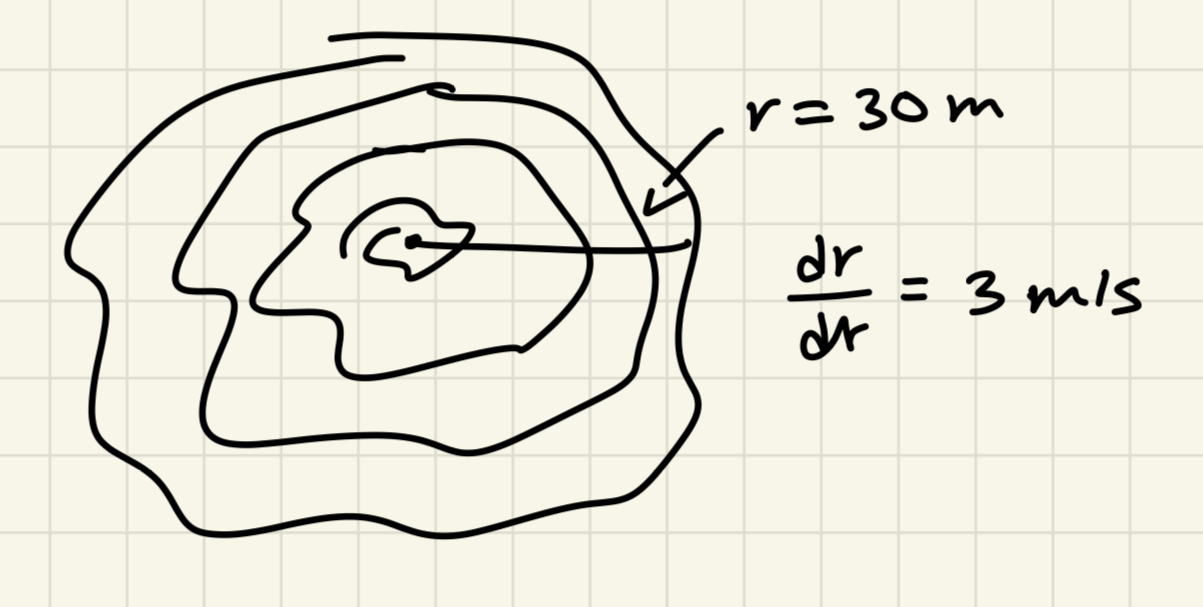
Image Courtesy of Sonia Sohail
Notice how the radius and rate of change of the radius are labeled in the image above. Labeling your quantities in relation to the picture is an excellent way to figure out the known and unknown quantities of the problem. Here, we see that the known quantities are the radius, which is 30 meters and the rate of change of radius with respect to time, denoted as , is 3 meters per second (m/s).
Because we are asked to find the area given the radius and its rate of change, we can model the relationship between the radius and the area of the oil spill using the formula for the area of a circle:
Since the problem explicitly states that the unknown quantity to solve for is how fast the area is increasing at a particular radius (r = 30), we can translate this as “the rate of change in the area with respect to time”, otherwise denoted as .
Now that we know what quantity we are looking for, we can begin differentiating the formula with respect to time. In finding the derivative of this formula, we use implicit differentiation to get:
For simplification, this can be written as
By this point, you may have noticed that we have most of the quantities that are present in this derivative, so we can substitute our values and solve for the unknown quantity. Make sure to include the units!
Therefore, our final answer is ✅
Practice Example #2
Here is another problem:
At first glance, this one may not be as clear as the previous one. This is what is known as the “ladder” problem. To understand what we are looking for, it is best, once again, to draw or model the problem, using the quantities provided in the question ✍️:
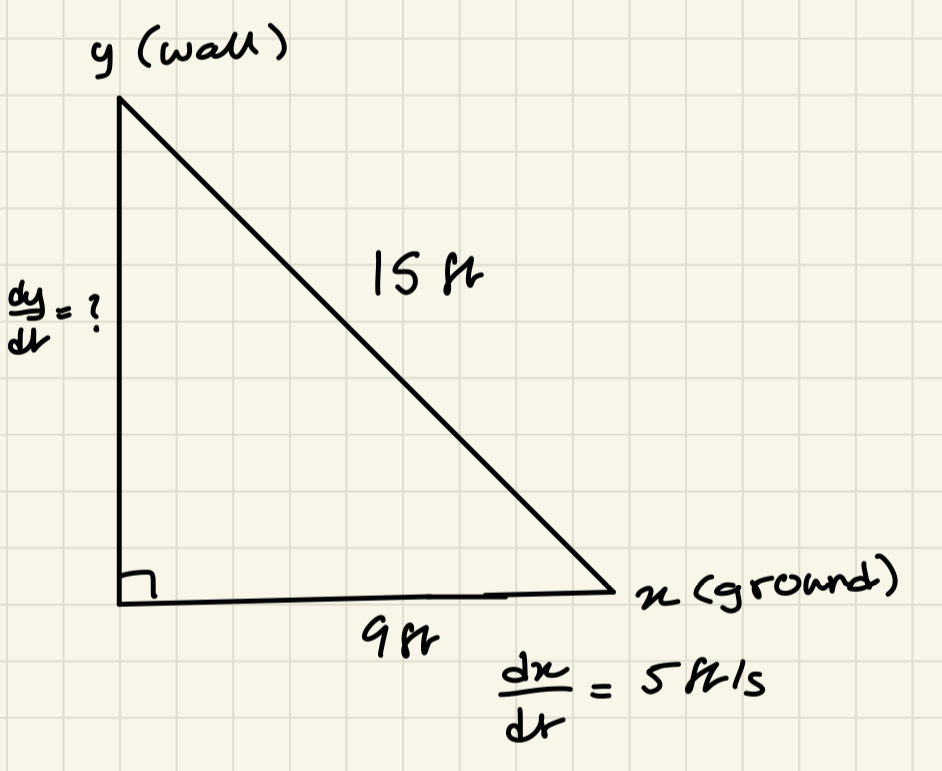
Image Courtesy of Sonia Sohail
Here we draw the ladder resting against the vertical y-axis with the bottom part of the ladder reaching the horizontal x-axis. In doing so, we have created a right triangle, and because we are given the length of the ladder (which could be considered the hypotenuse) and the length of one of the sides, we can use the Pythagorean Theorem to model the relationship between the lengths of the wall, the ground, and the ladder. 📐
Now that we have a formula that models our problem, we can see that our unknown quantity is the rate of change in y because as the ladder slides away from the wall (increasing the x-value), the length between the ground and the ladder is shrinking. This is denoted as . We can perform implicit differentiation on the formula to find the rate of change of all quantities with respect to time:
At this point, you may have noticed that while we have values for most of the quantities in this derivative, we still don't know what y is. You may think you’ve made a mistake somewhere, but all you need to do is solve for y using the original formula.
Given that , we can find the value of y by:
Now that we have the value of y, we can go back to our derivative and substitute the other values to solve for :
By substituting the values found for each of the quantities, we can use algebra to solve for , which is !
💫 Closing
Using the rules of differentiation, related rates is just one way to apply calculus to solving real-world problems. In the next guide, we’ll provide a different set of steps for you and additional practice questions. That way, you can decide what technique is best for you!
<< Hide Menu
4.4 Introduction to Related Rates
Using the concept of the rate of change, we can use derivatives to solve real-world problems particularly when dealing with how much something has changed in relation to another quantity. This is known as related rates in AP Calculus AB. 🧠
🤔 Using Derivative Rules
Related rates describe the process of using derivatives to calculate unknown quantities in relation to other quantities and their rates of change. Typically, problems regarding this topic are calculated concerning the quantity of time. ⏰
To solve related rate problems, several derivative rules must be applied, depending on the problem and the known and unknown quantities. This includes the chain rule, the Product Rule, and the Quotient Rule. For in-depth explanations, check out our previous study guides for explanations on these rules! They are all found in unit two, linked here.
✏️ How to Solve Related Rate Problems
Here is roughly a step-by-step process of solving related rates problems:
⛳️ Determine quantities from the problem
This includes known quantities where the amounts are explicitly mentioned in the problem and unknown quantities that are not mentioned in the problem.
📈 Model the relationship between quantities
This is done through a formula. It is important to note that if some quantities mentioned in the problem are not explicitly related to the unknown quantity that is trying to be solved, it should be replaced to simplify the formula when computing its derivatives.
👍 Apply derivative rules with respect to the unknown quantity
After coming up with a formula that encapsulates all of the quantities mentioned in the problem, use the derivative rules to derive the equation, its quantities, and their rates of change. Note that the variables in the formula must be derived WITH RESPECT to the same independent variable that is being solved (typically this is usually with respect to a variable of time .
🔢 Substitute known quantities into the derived equation & solve for the remaining quantities
Doing this will simplify the equation to the point where algebra can be applied to determine the value of unknown quantities.
This may be a lot to digest, so let’s go through a couple of examples to put this into action!
📝Related Rates Practice
Here are two practice problems you can use to get familiar with related rates.
Practice Example #1
Let’s start with an easy problem and work our way up!
To approach this problem, we can draw a picture or model of how this might look:

Image Courtesy of Sonia Sohail
Notice how the radius and rate of change of the radius are labeled in the image above. Labeling your quantities in relation to the picture is an excellent way to figure out the known and unknown quantities of the problem. Here, we see that the known quantities are the radius, which is 30 meters and the rate of change of radius with respect to time, denoted as , is 3 meters per second (m/s).
Because we are asked to find the area given the radius and its rate of change, we can model the relationship between the radius and the area of the oil spill using the formula for the area of a circle:
Since the problem explicitly states that the unknown quantity to solve for is how fast the area is increasing at a particular radius (r = 30), we can translate this as “the rate of change in the area with respect to time”, otherwise denoted as .
Now that we know what quantity we are looking for, we can begin differentiating the formula with respect to time. In finding the derivative of this formula, we use implicit differentiation to get:
For simplification, this can be written as
By this point, you may have noticed that we have most of the quantities that are present in this derivative, so we can substitute our values and solve for the unknown quantity. Make sure to include the units!
Therefore, our final answer is ✅
Practice Example #2
Here is another problem:
At first glance, this one may not be as clear as the previous one. This is what is known as the “ladder” problem. To understand what we are looking for, it is best, once again, to draw or model the problem, using the quantities provided in the question ✍️:

Image Courtesy of Sonia Sohail
Here we draw the ladder resting against the vertical y-axis with the bottom part of the ladder reaching the horizontal x-axis. In doing so, we have created a right triangle, and because we are given the length of the ladder (which could be considered the hypotenuse) and the length of one of the sides, we can use the Pythagorean Theorem to model the relationship between the lengths of the wall, the ground, and the ladder. 📐
Now that we have a formula that models our problem, we can see that our unknown quantity is the rate of change in y because as the ladder slides away from the wall (increasing the x-value), the length between the ground and the ladder is shrinking. This is denoted as . We can perform implicit differentiation on the formula to find the rate of change of all quantities with respect to time:
At this point, you may have noticed that while we have values for most of the quantities in this derivative, we still don't know what y is. You may think you’ve made a mistake somewhere, but all you need to do is solve for y using the original formula.
Given that , we can find the value of y by:
Now that we have the value of y, we can go back to our derivative and substitute the other values to solve for :
By substituting the values found for each of the quantities, we can use algebra to solve for , which is !
💫 Closing
Using the rules of differentiation, related rates is just one way to apply calculus to solving real-world problems. In the next guide, we’ll provide a different set of steps for you and additional practice questions. That way, you can decide what technique is best for you!

© 2025 Fiveable Inc. All rights reserved.