Browse By Unit
6.6 Applying Properties of Definite Integrals
1 min read•june 18, 2024
6.6 Applying Properties of Definite Integrals
Welcome back to AP Calculus! In this guide, we will be focusing on different definite integral properties and how to use various known integrals to determine an unknown definite integral. Although this may seem complicated at first, once you memorize the properties you will be able to answer any question that has to do with this topic!
💭 What is a Definite Integral?
Integrating a given function over the give interval to get a value (an actual number, rather than the integration + c) as a final answer. Another way to think about this is that you are finding the area of under on .
It is important to recognize what each of the terms above mean, so here is a quick summary!
-
The is the upper limit of integration, so it will always be the larger number in the given interval.
-
The is the lower limit of integration, so it will be the smaller number in the given interval.
-
is the function that are integration with respect to x.
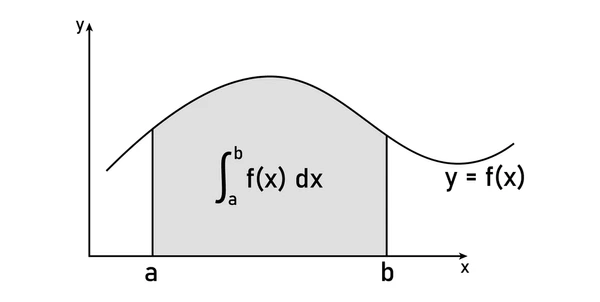
Image Courtesy of Shutterstock
📝 Definite Integral Properties
Here are the properties that should both be understood and memorized.
-
The Zero Rule: When the upper and lower integral are the same number, the integral is equal to zero. When thinking about this as finding the area under , if both limits of integration are the same then this creates a line and a line has no area.
-
If and are swapped on the integral (the lower limit is on top and the upper limit is on the bottom), you can rewrite the integral with and in the proper place if you negate the entire integral. When negating the integral, the two become equal to each other.
-
If there is a constant, k, with the function, you can bring it to the front of the integral and proceed as normal.
-
If there are two functions being added or subtracted as the integrand, you can take the integral of those two functions separately.
-
If the limits of integration go from and , you may solve for the integral by adding together an integral that goes from to and an integral that goes from to . This could be manipulated any way to solve for either integral.
An example of this manipulation can be seen below:
✏️ Properties of Definite Integral Walkthrough
If , , and find .
Let’s walk through this together!
We can set this up using property number five, as seen above. The limits of the integral that we are trying to find are 1 to 13. Since we are given the value of various integrals whose limits are between 1 to 13, we can add the integrals together to determine the value of the unknown integral.
✏️ Properties of Definite Integral Example 2
If , , find .
In this question, an integral whose limits go from 1 to 10 is given. We must instead find the value of one of the integrals whose limits are within that larger limit. This is the manipulation of property number five, and therefore this requires subtraction.
Great work! 👏
✏️ Properties of Definite Integral Example 3
If and , find .
We have to pay extra attention to the limits of integration in this question! Since one of the integrals goes from 10 to 6, we must rewrite it to ensure that 6 is placed as the lower limit since it is the smaller number according to property two.
Therefore this integral now becomes:
Now we can continue to do the question.
Understanding the properties is key to solving with definite integrals.
📝 Properties of Definite Integrals Practice Problems
Give each of these problems a try before moving on to the solutions!
- If , , and , find .
- If and , find
- If and , find .
Question 1 Solution
Question 2 Solution
Question 3 Solution
⭐ Closing
Once you learn the general idea of the concept, it becomes tough to overcomplicate, and therefore you can ace those multiple-choice questions (MCQs) when they come up. Practice the concept and you got this for the AP! ☺️
<< Hide Menu
6.6 Applying Properties of Definite Integrals
1 min read•june 18, 2024
6.6 Applying Properties of Definite Integrals
Welcome back to AP Calculus! In this guide, we will be focusing on different definite integral properties and how to use various known integrals to determine an unknown definite integral. Although this may seem complicated at first, once you memorize the properties you will be able to answer any question that has to do with this topic!
💭 What is a Definite Integral?
Integrating a given function over the give interval to get a value (an actual number, rather than the integration + c) as a final answer. Another way to think about this is that you are finding the area of under on .
It is important to recognize what each of the terms above mean, so here is a quick summary!
-
The is the upper limit of integration, so it will always be the larger number in the given interval.
-
The is the lower limit of integration, so it will be the smaller number in the given interval.
-
is the function that are integration with respect to x.

Image Courtesy of Shutterstock
📝 Definite Integral Properties
Here are the properties that should both be understood and memorized.
-
The Zero Rule: When the upper and lower integral are the same number, the integral is equal to zero. When thinking about this as finding the area under , if both limits of integration are the same then this creates a line and a line has no area.
-
If and are swapped on the integral (the lower limit is on top and the upper limit is on the bottom), you can rewrite the integral with and in the proper place if you negate the entire integral. When negating the integral, the two become equal to each other.
-
If there is a constant, k, with the function, you can bring it to the front of the integral and proceed as normal.
-
If there are two functions being added or subtracted as the integrand, you can take the integral of those two functions separately.
-
If the limits of integration go from and , you may solve for the integral by adding together an integral that goes from to and an integral that goes from to . This could be manipulated any way to solve for either integral.
An example of this manipulation can be seen below:
✏️ Properties of Definite Integral Walkthrough
If , , and find .
Let’s walk through this together!
We can set this up using property number five, as seen above. The limits of the integral that we are trying to find are 1 to 13. Since we are given the value of various integrals whose limits are between 1 to 13, we can add the integrals together to determine the value of the unknown integral.
✏️ Properties of Definite Integral Example 2
If , , find .
In this question, an integral whose limits go from 1 to 10 is given. We must instead find the value of one of the integrals whose limits are within that larger limit. This is the manipulation of property number five, and therefore this requires subtraction.
Great work! 👏
✏️ Properties of Definite Integral Example 3
If and , find .
We have to pay extra attention to the limits of integration in this question! Since one of the integrals goes from 10 to 6, we must rewrite it to ensure that 6 is placed as the lower limit since it is the smaller number according to property two.
Therefore this integral now becomes:
Now we can continue to do the question.
Understanding the properties is key to solving with definite integrals.
📝 Properties of Definite Integrals Practice Problems
Give each of these problems a try before moving on to the solutions!
- If , , and , find .
- If and , find
- If and , find .
Question 1 Solution
Question 2 Solution
Question 3 Solution
⭐ Closing
Once you learn the general idea of the concept, it becomes tough to overcomplicate, and therefore you can ace those multiple-choice questions (MCQs) when they come up. Practice the concept and you got this for the AP! ☺️

© 2025 Fiveable Inc. All rights reserved.