Browse By Unit
Remember earlier in this unit when you had to evaluate definite integrals? Now, imagine trying to solve a definite integral with one of the boundaries, instead of being an integer, being to infinity. How would you go about doing that? Today, we’ll learn about improper integrals and how to deal with these cases. 🚀
🟥 Recap: Definite Integrals
When coming across integration problems, you will encounter one of the following: an indefinite integral or a definite integral. Unlike indefinite integrals, which do not have boundaries, definite integrals have an upper and lower bound that can be plugged into your antiderivative to get a numerical value. Here are some examples of typical definite integrals you may have encountered in AP Calculus AB:
♾️ Evaluating Improper Integrals
An improper integral occurs when the limits of integration involve infinity or when the function being integrated becomes unbounded within the integration interval. This basically means that in the interval being evaluated, the function becomes unbounded to infinity.
In order to properly evaluate them, we must go back to Unit 1 and use limits. Limits allow for the evaluation of integral expressions where one or both of the boundaries are unbounded. When taking the limit of an improper integral, set the unbounded boundary to approach a letter and then take the limit from the lower bound to the upper bound:
Here are some steps to follow when evaluating improper integrals:
-
🤔 Identify the Issue: Determine whether the improper integral has one or both limits extending to infinity or if the integrand is unbounded within the integration interval.
-
✏️ Express as a Limit: If one or both limits are infinite, express the improper integral as a limit. For example, if integrating from a to infinity, rewrite it as the limit as b approaches infinity of the integral from a to b.
-
📐 Evaluate the Integral: Integrate the function as you normally would and apply the First Fundamental Theorem of Calculus:
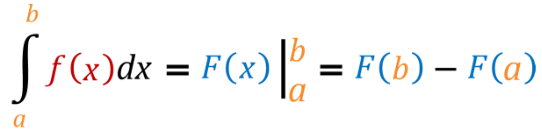
Image Courtesy of Calcworkshop
-
📏 Evaluate the Limit: Now, evaluate the limit that you've introduced in step 2. This involves considering what happens to the integral as the bound approaches its infinite or unbounded value.
-
🏁 Check for Convergence: Determine whether the limit converges or diverges. If the limit approaches a finite value, the improper integral converges; if it approaches infinity or doesn't exist, it diverges.
🧠 Improper Integrals Example 1
🤔 Step 1) Identify the Issue:
In the integral above, the graph is unbounded at x=0.
✏️ Step 2) Express as a Limit:
📐 Step 3) Evaluate the Integral:
📏 Step 4) Evaluate the Limit:
🏁 Step 5) Check for Convergence:
The limit approaches 2, a finite number, which means the improper integral converges at 2.
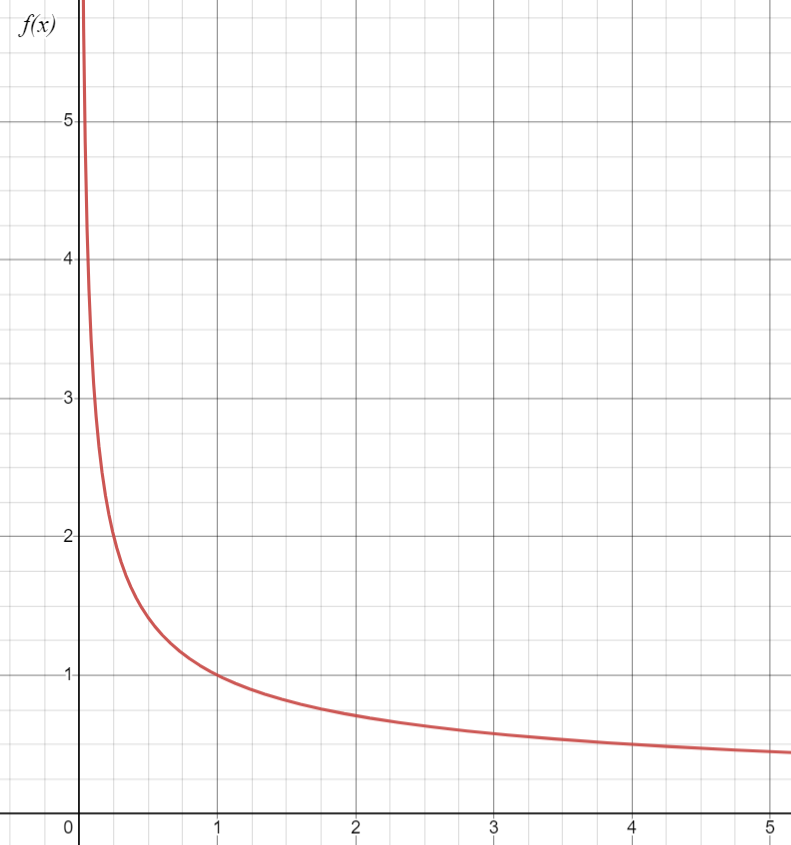
Image Courtesy of Desmos
🧠 Improper Integrals Example 2
Find the area of the function from to or state that it converges.
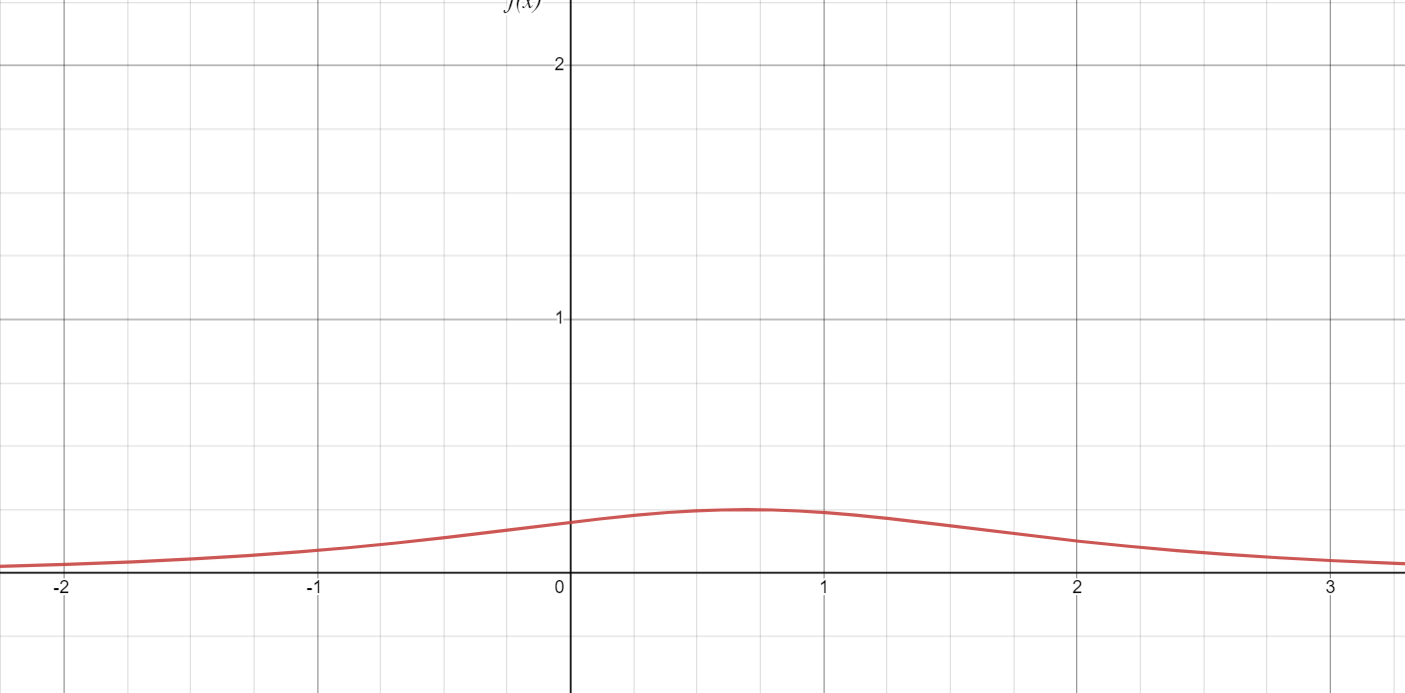
Image Courtesy of Desmos
Since both the upper and lower boundaries are unbounded, we must split the integral into two by choosing an arbitrary point in between the bounds. By choosing (the global maximum of the function), we make it so both to the left and the right of are equal in area, so we only have to manipulate one side of the integral:
So, the area of this unbounded shaded region is . Great job! 🤗
🖊️ 2017 AP Calc Exam #5c Walkthrough
The following free-response question (FRQ) is Question 5 (c) from the 2017 AP Calculus BC Examination administered by College Board. All credit to College Board.
Let be the function defined by…
Using the following identity, evaluate or show that the integral diverges.
Let’s go through it! ⬇️
To solve this question, all we must do is express the integral as a limit and determine whether or not it diverges.
Because the partial fraction is already given to us, all we must do is substitute it into our integrand and solve normally:
Awesome work! 👍
⭐️ Closing
Well done! You have now learned how to successfully evaluate improper integrals and distinguish whether or not the area of these integrals converge or diverge. Make sure to keep practicing and improving your skills. 😊
<< Hide Menu
Remember earlier in this unit when you had to evaluate definite integrals? Now, imagine trying to solve a definite integral with one of the boundaries, instead of being an integer, being to infinity. How would you go about doing that? Today, we’ll learn about improper integrals and how to deal with these cases. 🚀
🟥 Recap: Definite Integrals
When coming across integration problems, you will encounter one of the following: an indefinite integral or a definite integral. Unlike indefinite integrals, which do not have boundaries, definite integrals have an upper and lower bound that can be plugged into your antiderivative to get a numerical value. Here are some examples of typical definite integrals you may have encountered in AP Calculus AB:
♾️ Evaluating Improper Integrals
An improper integral occurs when the limits of integration involve infinity or when the function being integrated becomes unbounded within the integration interval. This basically means that in the interval being evaluated, the function becomes unbounded to infinity.
In order to properly evaluate them, we must go back to Unit 1 and use limits. Limits allow for the evaluation of integral expressions where one or both of the boundaries are unbounded. When taking the limit of an improper integral, set the unbounded boundary to approach a letter and then take the limit from the lower bound to the upper bound:
Here are some steps to follow when evaluating improper integrals:
-
🤔 Identify the Issue: Determine whether the improper integral has one or both limits extending to infinity or if the integrand is unbounded within the integration interval.
-
✏️ Express as a Limit: If one or both limits are infinite, express the improper integral as a limit. For example, if integrating from a to infinity, rewrite it as the limit as b approaches infinity of the integral from a to b.
-
📐 Evaluate the Integral: Integrate the function as you normally would and apply the First Fundamental Theorem of Calculus:
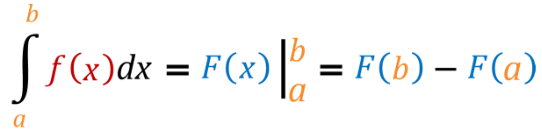
Image Courtesy of Calcworkshop
-
📏 Evaluate the Limit: Now, evaluate the limit that you've introduced in step 2. This involves considering what happens to the integral as the bound approaches its infinite or unbounded value.
-
🏁 Check for Convergence: Determine whether the limit converges or diverges. If the limit approaches a finite value, the improper integral converges; if it approaches infinity or doesn't exist, it diverges.
🧠 Improper Integrals Example 1
🤔 Step 1) Identify the Issue:
In the integral above, the graph is unbounded at x=0.
✏️ Step 2) Express as a Limit:
📐 Step 3) Evaluate the Integral:
📏 Step 4) Evaluate the Limit:
🏁 Step 5) Check for Convergence:
The limit approaches 2, a finite number, which means the improper integral converges at 2.

Image Courtesy of Desmos
🧠 Improper Integrals Example 2
Find the area of the function from to or state that it converges.

Image Courtesy of Desmos
Since both the upper and lower boundaries are unbounded, we must split the integral into two by choosing an arbitrary point in between the bounds. By choosing (the global maximum of the function), we make it so both to the left and the right of are equal in area, so we only have to manipulate one side of the integral:
So, the area of this unbounded shaded region is . Great job! 🤗
🖊️ 2017 AP Calc Exam #5c Walkthrough
The following free-response question (FRQ) is Question 5 (c) from the 2017 AP Calculus BC Examination administered by College Board. All credit to College Board.
Let be the function defined by…
Using the following identity, evaluate or show that the integral diverges.
Let’s go through it! ⬇️
To solve this question, all we must do is express the integral as a limit and determine whether or not it diverges.
Because the partial fraction is already given to us, all we must do is substitute it into our integrand and solve normally:
Awesome work! 👍
⭐️ Closing
Well done! You have now learned how to successfully evaluate improper integrals and distinguish whether or not the area of these integrals converge or diverge. Make sure to keep practicing and improving your skills. 😊

© 2025 Fiveable Inc. All rights reserved.