Browse By Unit
6.10 Integrating Functions Using Long Division and Completing the Square
1 min read•june 18, 2024
6.10 Integrating Functions Using Long Division and Completing the Square
Ever find yourself dealing with a tricky integral that doesn't seem possible with techniques you’re familiar with? This is when your knowledge of Algebra and Precalculus comes in handy. As you’ll learn today, it is possible to use techniques such as polynomial long division and completing the square to rearrange integral expressions into simpler, more approachable problems to solve. 🙌
➗ Integrating Using Long Division
If you can recall from Precalculus, a rational function has a polynomial in the numerator and the denominator of the function. A good rule of thumb is if the numerator of the rational function is an equal degree or higher than the denominator, long division might be the way to go.
✏️ Integrating Using Long Division Walkthrough
Solve the integral expression:
First things first, we can see that we have a rational function, where the degree in the numerator is higher than that of the denominator. Let’s go ahead and solve it with long division!
Since we can see a quadratic function in the numerator and a linear function in the denominator, we can use long division to simplify this integral:
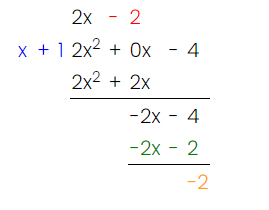
Image Courtesy of MathCelebrity
Now, replace your integrand with the answer from your polynomial division:
Great job! You can now identify and solve integrals involving long division. 😊
Usually, these problems appear in the multiple-choice section and a quick look at the answer options can tell you that you may be looking at a long-division integral. If you see multiple answer options that start off as polynomials and end with a natural log term, that is a strong indicator of a long-division integral. For the last several years, this type of problem has appeared, at most, as one problem in the multiple-choice section.
🟦 Integrating Using Complete the Square
If you come across an integral with a quadratic expression in the integrand, and it's missing a perfect square term, completing the square could be very helpful. Manipulating the quadratic expression by adding and subtracting the right value allows you to simplify the integral and make it more manageable. This is commonly seen in integral expressions that end up being inverse trigonometric functions.
✏️ Integrating Using Complete the Square Walkthrough
Solve the integral expression:
First, complete the square of the denominator, which is currently a quadratic expression. To complete the square, we want it in the form .
Next, we need to place it into the integrand:
The next step is not necessarily intuitive. You should be starting to sense that we are heading towards an inverse trig solution. As such, making the numerator a 1 would make the integral easier.
You may start to realize that this integral can be manipulated to resemble the integral of :
Compare what you have with this integral and you’ll see that and . Substitute these into the formula. Remember to multiply the whole integral by the constant in the numerator, which is 4 in this case.
Awesome work!!
⭐ Practice Problems
Practice #1
Evaluate the following integral.
And here’s the work for it!
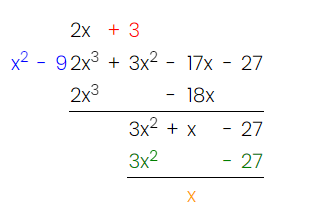
Image Courtesy of MathCelebrity
Practice #2
Evaluate the following integral.
This time, integrate by completing the square.
Practice #3
Evaluate the following integral.
Last but not least, another long-division question!
Image Courtesy of MathCelebrity
🔷 Closing
Well done! 🎉
You can now successfully integrate expressions that require you to complete the square and do long division to simplify the integrand. These problems can get pretty convoluted, so it is important to get enough practice with them. Happy studying!
<< Hide Menu
6.10 Integrating Functions Using Long Division and Completing the Square
1 min read•june 18, 2024
6.10 Integrating Functions Using Long Division and Completing the Square
Ever find yourself dealing with a tricky integral that doesn't seem possible with techniques you’re familiar with? This is when your knowledge of Algebra and Precalculus comes in handy. As you’ll learn today, it is possible to use techniques such as polynomial long division and completing the square to rearrange integral expressions into simpler, more approachable problems to solve. 🙌
➗ Integrating Using Long Division
If you can recall from Precalculus, a rational function has a polynomial in the numerator and the denominator of the function. A good rule of thumb is if the numerator of the rational function is an equal degree or higher than the denominator, long division might be the way to go.
✏️ Integrating Using Long Division Walkthrough
Solve the integral expression:
First things first, we can see that we have a rational function, where the degree in the numerator is higher than that of the denominator. Let’s go ahead and solve it with long division!
Since we can see a quadratic function in the numerator and a linear function in the denominator, we can use long division to simplify this integral:
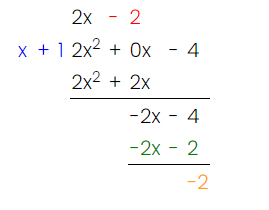
Image Courtesy of MathCelebrity
Now, replace your integrand with the answer from your polynomial division:
Great job! You can now identify and solve integrals involving long division. 😊
Usually, these problems appear in the multiple-choice section and a quick look at the answer options can tell you that you may be looking at a long-division integral. If you see multiple answer options that start off as polynomials and end with a natural log term, that is a strong indicator of a long-division integral. For the last several years, this type of problem has appeared, at most, as one problem in the multiple-choice section.
🟦 Integrating Using Complete the Square
If you come across an integral with a quadratic expression in the integrand, and it's missing a perfect square term, completing the square could be very helpful. Manipulating the quadratic expression by adding and subtracting the right value allows you to simplify the integral and make it more manageable. This is commonly seen in integral expressions that end up being inverse trigonometric functions.
✏️ Integrating Using Complete the Square Walkthrough
Solve the integral expression:
First, complete the square of the denominator, which is currently a quadratic expression. To complete the square, we want it in the form .
Next, we need to place it into the integrand:
The next step is not necessarily intuitive. You should be starting to sense that we are heading towards an inverse trig solution. As such, making the numerator a 1 would make the integral easier.
You may start to realize that this integral can be manipulated to resemble the integral of :
Compare what you have with this integral and you’ll see that and . Substitute these into the formula. Remember to multiply the whole integral by the constant in the numerator, which is 4 in this case.
Awesome work!!
⭐ Practice Problems
Practice #1
Evaluate the following integral.
And here’s the work for it!
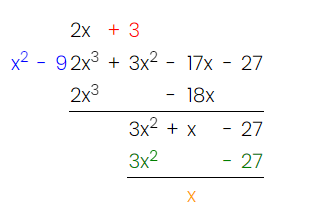
Image Courtesy of MathCelebrity
Practice #2
Evaluate the following integral.
This time, integrate by completing the square.
Practice #3
Evaluate the following integral.
Last but not least, another long-division question!
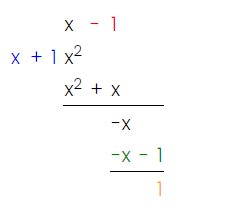
Image Courtesy of MathCelebrity
🔷 Closing
Well done! 🎉
You can now successfully integrate expressions that require you to complete the square and do long division to simplify the integrand. These problems can get pretty convoluted, so it is important to get enough practice with them. Happy studying!

© 2025 Fiveable Inc. All rights reserved.