Browse By Unit
6.5 Interpreting the Behavior of Accumulation Functions Involving Area
1 min read•june 18, 2024
6.5 Interpreting the Behavior of Accumulation Functions Involving Area
Welcome back to AP Calculus! 🌶️
In this guide, we'll analyze the behavior of accumulation functions using the Fundamental Theorem of Calculus. We'll focus on graphical, numerical, analytical, and verbal representations to gain a comprehensive understanding of integrally-defined functions.
👩🏫The Fundamental Theorem Of Calculus
The Fundamental Theorem of Calculus links accumulation functions, which are adapted from infinite Riemann sums, to antiderivatives, which “undo” a derivative. This theory states that if
Then,
The first equation above states that is the accumulation function of which equals the area under the curve of between the boundaries made by the lines and . Here, a is some constant number while n is a variable. Visually, this looks like the following:
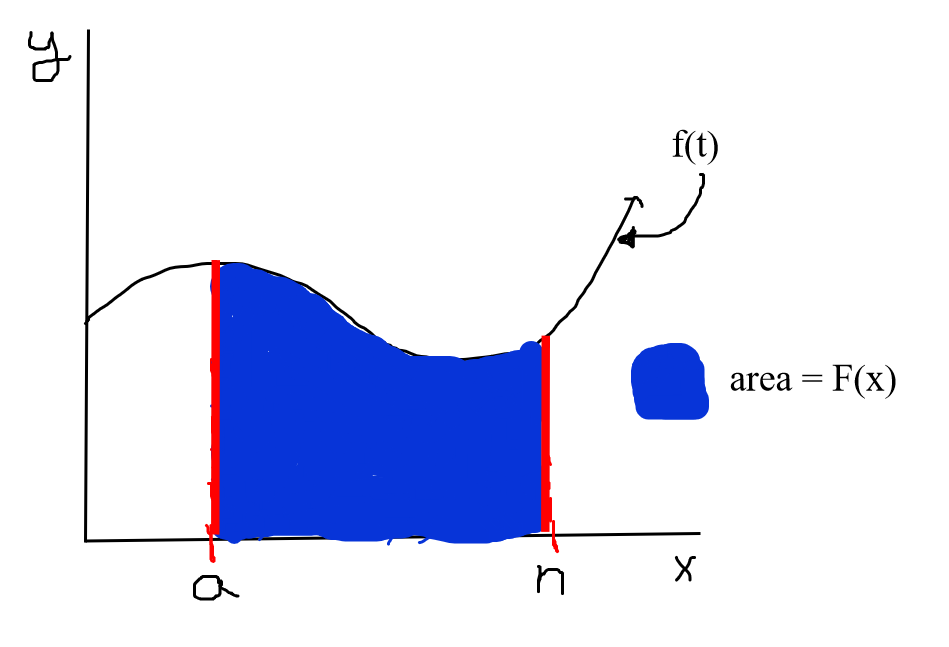
Image Courtesy of Julianna Fontanilla
The second equation says that the derivative of is . This also means that the antiderivative of is , and that .
To put these 2 pieces of information together, the area under a function is equal to the value of its antiderivative (calculated with the same bounds, of course).
📒 Using the Fundamental Theorem Of Calculus
Just like previous functions, these integrally defined functions can be defined by their various characteristics listed below. Some AP multiple-choice or free-response questions will ask you to analyze these factors given a graph or a function with an integral.
Quick Refresher Chart
| If F(x) is… | then F’(x) | and F’'(x) |
| Increasing | + | ——— |
| Decreasing | - | ——— |
| Relative Maximum | 0 and changes from + to - | is - |
| Relative Minimum | 0 and changes from - to + | is + |
| Concave Up | ——— | is + |
| Concave Down | ——— | is - |
| Inflection Point | ——— | Changes Sign |
It’s important to note that finding increasing/decreasing ranges uses the first derivative while finding concave up/down ranges uses the second derivative. In addition, a relative minimum or maximum cannot be an inflection point.
When working with analysis integral problems where you must find one of the above items in the table remember that you are working backwards. Instead of finding or drawing the derivative of the given numerical graph or function, use the information as the already-found derivative of your target integral. For example, if you are told that
Realize that is equal to the first derivative and find critical points or the second derivative accordingly.
🤔 Practicing with Accumulation Functions
Almost all AP questions on this topic will fall into 1 of 3 types: graph, table, or equation. These are all equally likely to occur. We will be going over a graph problem!
📈 Graph Questions
Graph questions almost always tell you that a function and give you a graph or image of the function .
The most important thing to remember with this type of problem is that the graph given is not your target function. Instead, the graph is the derivative of your target function. Let’s try an official College Board FRQ from the 2022 exam! (All credits to College Board.)
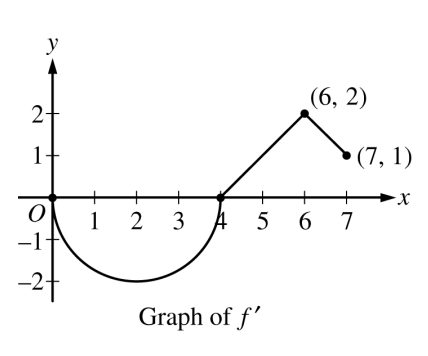
Courtesy of College Board
Let be a differentiable function with . On the interval , the graph of , the derivative of , consists of a semicircle and two line segments, as shown in the figure above.
(a) Find and .
(b) Find the x-coordinates of all points of inflection on the graph of for . Justify your answer.
(c) Let be the function defined by . On what intervals, if any, is decreasing for ? Show the analysis that leads to your answer.
(d) For the function defined in part (c), find the absolute minimum value on the interval . Justify your answer.
AP Calc 2022 #3a
Part A of this question asks us to find and . Since we are told that the graph above is the graph of , this means that the original equation of…
Using the Fundamental Theorem of Calculus, we know that this equation is equal to the accumulation function, and is represented on the graph by the area between the curve and the x-axis. This area is the change in over the given bounds.
Using mathematical operations, we can set up 2 equations to find and .
The first equation is
which can be simplified to
We know that from the problem and that is the area under between x = 0 and x = 4, given the definition of the accumulation function. Our problem tells us that is composed of a semicircle and 2 line segments, and we can see that the area between 0 and 4 is the semicircle area. The area of this semicircle is
Remember that since this area is below the x-axis, it is considered negative!
Plugging this into the our equation above gives
In the same way, you can set up your equation for .
Again, we know that . The area of from and lies on the first straight line which has a slope of , using the known points of (4,0) and (6,2). Using this information in a slope equation OR by looking at the graph, we know that when then . This means that the triangle area between and has a height of 1 and a width of 1, with a total area of . Putting this into our earlier equation, we get
Remember to write down your integrals AND label your final answers as f(0) and f(5) to earn all points on the free-response portion!
AP Calc 2022 #3b
This part asks for the x-coordinates of any points of inflection of the function . Since we are given the graph of , we need to look at the derivative of this graph to find points of inflection (2nd derivative) of the original function .
Remember that points of inflection occur when the second derivative of a function changes signs. On the graph given to us, this occurs where the slope of the derivative changes signs. This occurs at x = 2, where the slope changes from negative to positive, and x = 6, where the slope changes from positive to negative. Since the slope of a function at a point is the 1st derivative, the slope of the first derivative at a point is the second derivative!
AP Calc 2022 #3c
Our new equation is defined by
so the new derivative is
A function is decreasing when its derivative is negative, so g(x) is decreasing when
or
According to the graph, this occurs between .
AP Calc 2022 #3d
This part asks for the absolute minimum function of . A local minimum occurs when and changes from negative to positive. Our candidates are the two endpoints of and as well as the local minimum . Just as a reminder, so when which only occurs within the function when .
Testing all 3 candidates for the absolute minimum gives…
| x | f(x) | g(x) = f(x) -x |
| 0 | 3 + 2pi | 3 + 2pi |
| 5 | 3.5 | 3.5 - 5 = -1.5 |
| 7 | 7.5 | 6.5 -7 =-0.5 |
and were both imported from Part A.
was found by adding through geometry.
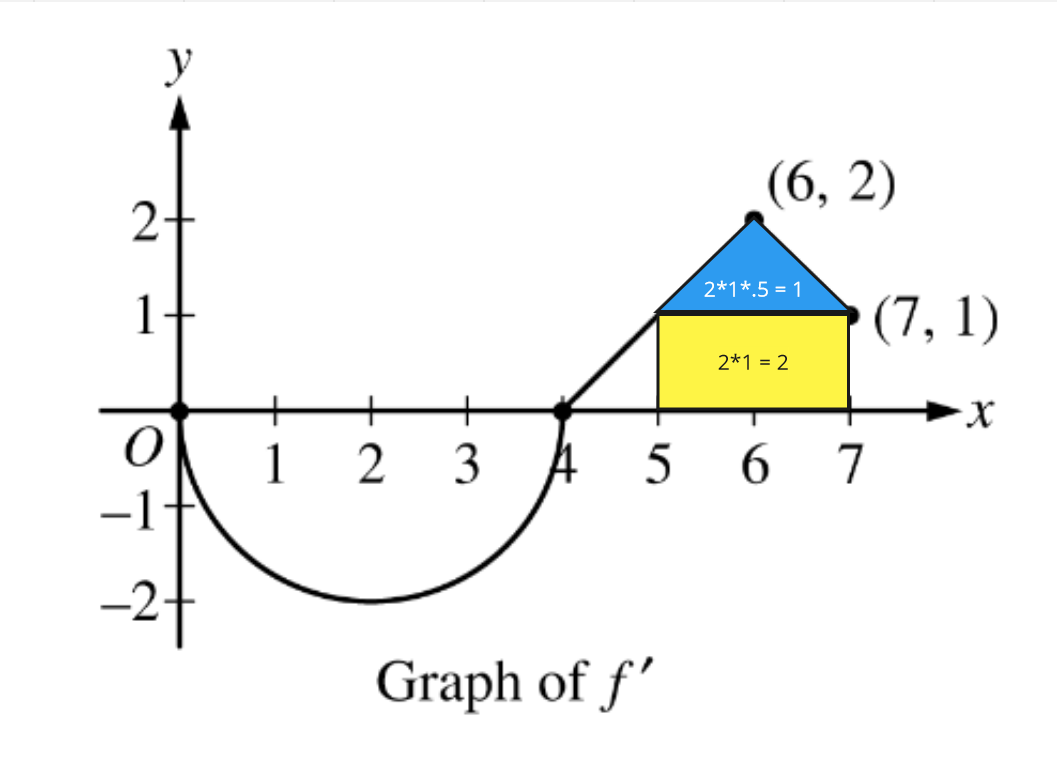
Courtesy of College Board and Julianna Fontanilla
So the absolute minimum of is -1.5 which occurs when .
📝 Practice Tips
Here are some tips and tricks when approaching these question types:
- 💭 Understand the Relationship: If , this means that and .
- 📈 Use Graphical Information: Identify notable points on a graph, such as zeroes, minimums, and maximums. Always relate these back to the original integral equation.
- 🧠 Evaluate Extrema: Evaluate function values at critical points (zeroes) to determine relative and absolute extrema of the original integral. Don’t forget to also evaluate endpoints!
- ✅ Clarify the Question: Make sure you are looking for the zeroes of the correct derivative! It gets very easy to confuse F(x), F’(x), and F’’(x). Write Tip 1 somewhere on your paper.
This topic may be difficult, but the most important thing to remember is that area under a curve = the antiderivative. Practice using both concepts with different integral questions to get comfortable with the idea. As always, the best way to improve your understanding is to try lots of practice problems and familiarize yourself with the setup of common AP questions covering this topic. You’ve got this! 👍🏼
<< Hide Menu
6.5 Interpreting the Behavior of Accumulation Functions Involving Area
1 min read•june 18, 2024
6.5 Interpreting the Behavior of Accumulation Functions Involving Area
Welcome back to AP Calculus! 🌶️
In this guide, we'll analyze the behavior of accumulation functions using the Fundamental Theorem of Calculus. We'll focus on graphical, numerical, analytical, and verbal representations to gain a comprehensive understanding of integrally-defined functions.
👩🏫The Fundamental Theorem Of Calculus
The Fundamental Theorem of Calculus links accumulation functions, which are adapted from infinite Riemann sums, to antiderivatives, which “undo” a derivative. This theory states that if
Then,
The first equation above states that is the accumulation function of which equals the area under the curve of between the boundaries made by the lines and . Here, a is some constant number while n is a variable. Visually, this looks like the following:

Image Courtesy of Julianna Fontanilla
The second equation says that the derivative of is . This also means that the antiderivative of is , and that .
To put these 2 pieces of information together, the area under a function is equal to the value of its antiderivative (calculated with the same bounds, of course).
📒 Using the Fundamental Theorem Of Calculus
Just like previous functions, these integrally defined functions can be defined by their various characteristics listed below. Some AP multiple-choice or free-response questions will ask you to analyze these factors given a graph or a function with an integral.
Quick Refresher Chart
| If F(x) is… | then F’(x) | and F’'(x) |
| Increasing | + | ——— |
| Decreasing | - | ——— |
| Relative Maximum | 0 and changes from + to - | is - |
| Relative Minimum | 0 and changes from - to + | is + |
| Concave Up | ——— | is + |
| Concave Down | ——— | is - |
| Inflection Point | ——— | Changes Sign |
It’s important to note that finding increasing/decreasing ranges uses the first derivative while finding concave up/down ranges uses the second derivative. In addition, a relative minimum or maximum cannot be an inflection point.
When working with analysis integral problems where you must find one of the above items in the table remember that you are working backwards. Instead of finding or drawing the derivative of the given numerical graph or function, use the information as the already-found derivative of your target integral. For example, if you are told that
Realize that is equal to the first derivative and find critical points or the second derivative accordingly.
🤔 Practicing with Accumulation Functions
Almost all AP questions on this topic will fall into 1 of 3 types: graph, table, or equation. These are all equally likely to occur. We will be going over a graph problem!
📈 Graph Questions
Graph questions almost always tell you that a function and give you a graph or image of the function .
The most important thing to remember with this type of problem is that the graph given is not your target function. Instead, the graph is the derivative of your target function. Let’s try an official College Board FRQ from the 2022 exam! (All credits to College Board.)

Courtesy of College Board
Let be a differentiable function with . On the interval , the graph of , the derivative of , consists of a semicircle and two line segments, as shown in the figure above.
(a) Find and .
(b) Find the x-coordinates of all points of inflection on the graph of for . Justify your answer.
(c) Let be the function defined by . On what intervals, if any, is decreasing for ? Show the analysis that leads to your answer.
(d) For the function defined in part (c), find the absolute minimum value on the interval . Justify your answer.
AP Calc 2022 #3a
Part A of this question asks us to find and . Since we are told that the graph above is the graph of , this means that the original equation of…
Using the Fundamental Theorem of Calculus, we know that this equation is equal to the accumulation function, and is represented on the graph by the area between the curve and the x-axis. This area is the change in over the given bounds.
Using mathematical operations, we can set up 2 equations to find and .
The first equation is
which can be simplified to
We know that from the problem and that is the area under between x = 0 and x = 4, given the definition of the accumulation function. Our problem tells us that is composed of a semicircle and 2 line segments, and we can see that the area between 0 and 4 is the semicircle area. The area of this semicircle is
Remember that since this area is below the x-axis, it is considered negative!
Plugging this into the our equation above gives
In the same way, you can set up your equation for .
Again, we know that . The area of from and lies on the first straight line which has a slope of , using the known points of (4,0) and (6,2). Using this information in a slope equation OR by looking at the graph, we know that when then . This means that the triangle area between and has a height of 1 and a width of 1, with a total area of . Putting this into our earlier equation, we get
Remember to write down your integrals AND label your final answers as f(0) and f(5) to earn all points on the free-response portion!
AP Calc 2022 #3b
This part asks for the x-coordinates of any points of inflection of the function . Since we are given the graph of , we need to look at the derivative of this graph to find points of inflection (2nd derivative) of the original function .
Remember that points of inflection occur when the second derivative of a function changes signs. On the graph given to us, this occurs where the slope of the derivative changes signs. This occurs at x = 2, where the slope changes from negative to positive, and x = 6, where the slope changes from positive to negative. Since the slope of a function at a point is the 1st derivative, the slope of the first derivative at a point is the second derivative!
AP Calc 2022 #3c
Our new equation is defined by
so the new derivative is
A function is decreasing when its derivative is negative, so g(x) is decreasing when
or
According to the graph, this occurs between .
AP Calc 2022 #3d
This part asks for the absolute minimum function of . A local minimum occurs when and changes from negative to positive. Our candidates are the two endpoints of and as well as the local minimum . Just as a reminder, so when which only occurs within the function when .
Testing all 3 candidates for the absolute minimum gives…
| x | f(x) | g(x) = f(x) -x |
| 0 | 3 + 2pi | 3 + 2pi |
| 5 | 3.5 | 3.5 - 5 = -1.5 |
| 7 | 7.5 | 6.5 -7 =-0.5 |
and were both imported from Part A.
was found by adding through geometry.

Courtesy of College Board and Julianna Fontanilla
So the absolute minimum of is -1.5 which occurs when .
📝 Practice Tips
Here are some tips and tricks when approaching these question types:
- 💭 Understand the Relationship: If , this means that and .
- 📈 Use Graphical Information: Identify notable points on a graph, such as zeroes, minimums, and maximums. Always relate these back to the original integral equation.
- 🧠 Evaluate Extrema: Evaluate function values at critical points (zeroes) to determine relative and absolute extrema of the original integral. Don’t forget to also evaluate endpoints!
- ✅ Clarify the Question: Make sure you are looking for the zeroes of the correct derivative! It gets very easy to confuse F(x), F’(x), and F’’(x). Write Tip 1 somewhere on your paper.
This topic may be difficult, but the most important thing to remember is that area under a curve = the antiderivative. Practice using both concepts with different integral questions to get comfortable with the idea. As always, the best way to improve your understanding is to try lots of practice problems and familiarize yourself with the setup of common AP questions covering this topic. You’ve got this! 👍🏼

© 2025 Fiveable Inc. All rights reserved.