Browse By Unit
6.3 Riemann Sums, Summation Notation, and Definite Integral Notation
1 min read•june 18, 2024
Emery
Emery
6.3 Riemann Sums, Summation Notation, and Definite Integral Notation
So far in Unit 6, we’ve learned how to approximate the area under the curve. But what if we wanted to find its exact value? For that, we’ll need to learn about integrals and how they are related to the Riemann sum. We’re bringing limits back! 🧠
Σ Summation Notation
Before we get into integrals, we first need to learn how to make taking a Riemann sum faster. To do this, we’ll introduce summation notation so that we can apply algebra instead of manually computing the Riemann sum.
Let’s consider the function over the interval 0 to 5:
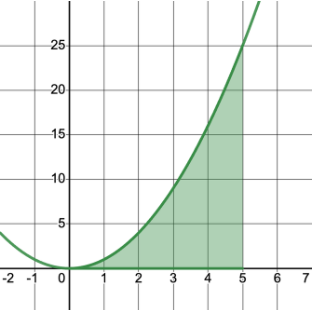
Image courtesy of Emery
Now, let’s use a left Riemann sum with 5 subintervals to approximate this area.
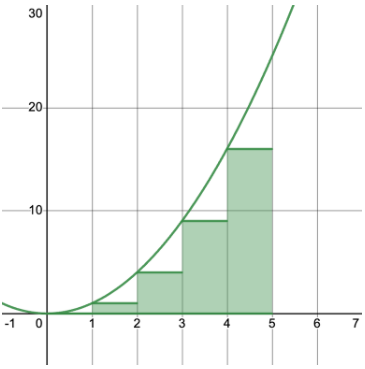
Image courtesy of Emery
To convert this to summation notation, we need to create a function that will give us the area of each rectangle. For now, let’s name this function so that gives us the area of the th rectangle. With this function, we can write the Riemann sum as:
Now that we have our summation notation, we need to find an expression for . We know that the area of the rectangle will be , where is the width of the base and is the height.
The width of our base will be constant, and we can find it by dividing the entire interval by the number of subintervals we want:
The height is a little more tricky to notate, but it is just the value of the function at each of the left endpoints. To find this next (or th) point, let’s first find the -value, which we’ll denote as . To do this, we start at 0 and repeatedly add 1, the length of our subinterval.
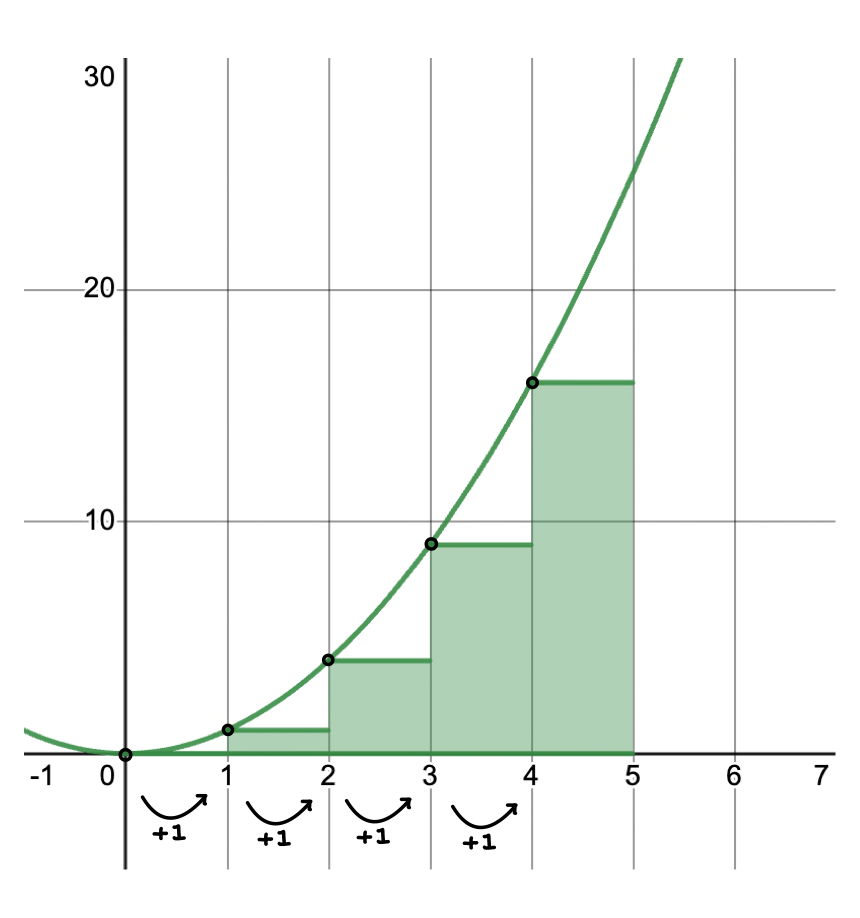
Image courtesy of Emery
We can write the formula for this -value as or just . We can obtain the -value, or height, by simply plugging in this formula for the -value to our original formula like so: .
We can put these two things together in the area formula as:
which simplifies to
Now, we simply plug that back into our summation notation:
✏️ General Form of Riemann Sum
The general form for the Riemann sum in summation notation is as follows:
for left-endpoint, and
for right-endpoint.
Let’s break down what each symbol means!
- : This denotes the number of subintervals, and is usually given in the problem
- : The lower bound of the interval.
- : The upper bound of the interval.
- : This is the width of each subinterval, and can be calculated by using the formula .
- : This denotes the right endpoint for each rectangle, such that .
- : The original function with plugged in.
- : Tells us to add up the values from for left Riemann sums or for right Riemann sums.
Whew! That’s a lot of pieces to put together. 🧩
∫ Connecting to Definite Integrals
We learned in the last lesson that our Riemann sum becomes more precise if we use more rectangles or a greater value for . But what if we could have infinite rectangles, with infinitely tiny widths?
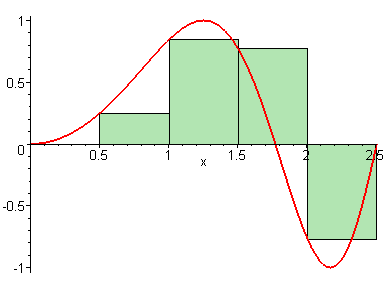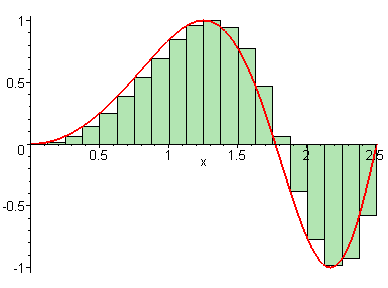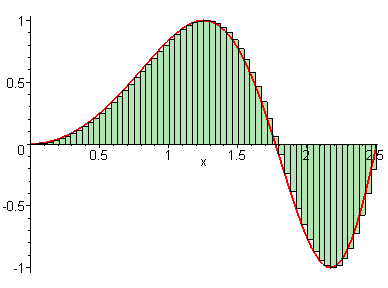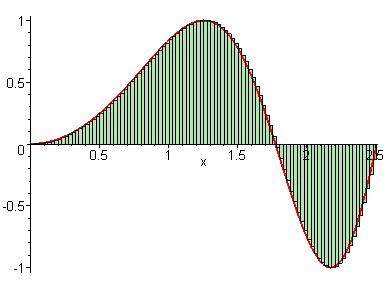
GIF courtesy of Maplesoft
We see that as , our approximation for the area under the curve gets closer and closer to perfect. This means that we can connect the Riemann sum to the definite integral like so:
Where and .
The truly amazing thing is that this limit tells us the exact value for the definite integral—not just an approximation! 👌
📌 Connecting to Definite Integrals Walkthrough
Let’s connect all the dots and practice converting from summation to definite integral notation with this example problem!
Given the function over the interval , give the summation notation for the right Riemann sum using 10 subintervals and calculate its value. Then, write the definite integral as the limit of the right Riemann sum as approaches infinity.
1) Solving Summation Notation
The first part of the problem asks us to give and solve the summation notation with a fixed, finite . Let’s first write the general form without our area function defined:
Now, we need to define our terms, starting with , which is defined as . Then, we need to define so that we can plug it into the original equation. To get the th right endpoint, we use the formula . In our case, and , so . Now, we plug that back into our original equation to find that . Putting it all together, we find that the right Riemann sum using 10 subintervals is:
The next part of the problem asks us to calculate this sum. This sum essentially tells us to plug in values from 1 to 10 and sum them all up, like so:
This can be rewritten as
Lots of math, but not too bad, right?
2) Writing the Definite Integral
The final part of the problem asks us to write the definite integral as the limit of the right Riemann sum as approaches infinity. First, let’s write the definite integral:
Now, let’s remind ourselves of the general form for equation definite integrals to Riemann sums:
This is where things get a little tricky—since is the variable of our limit, we need to define our other terms in terms of .
- Let’s start by first defining as .
- Then, let’s define in terms of , too. .
- Now let’s plug that back into to find that .
Finally, let’s put that all back into our equation to get:
These problems take a lot of practice, but once you commit the process for finding and to memory, they become very doable. Good luck! 🍀
✏️ Riemann Sum Practice
Try to tackle these three problems yourself! When you’re done, you can check out the solutions and how to walk through them.
❓Practice Problems
- For the function , determine the definite integral as the limit of a Riemann sum.
- Express the definite integral dx as the limit of a Riemann sum.
- The velocity function is given by for the time interval . Express the definite integral as the limit of a Riemann sum.
Answers below! ⬇️
📝 Solutions
Practice Problem 1 Solution
Start by defining in terms of : . Then, do the same for : . Then, plug this in to to get:
Finally, plug this all into the general limit equation to find that:
The next question follows a very similar process.
Practice Problem 2 Solution
You can again start by defining in terms of : . Then, do the same for : . Then, plug this in to to get:
Finally, plug this all into the general limit equation to find that:
Practice Problem 3 Solution
Last question! Start by defining in terms of : . Then, do the same for : . Then, plug this in to to get:
Finally, plug this all into the general limit equation to find that:
💫 Closing
Now that you’ve completed this guide, you should feel comfortable expressing Riemann sums using summation notation, understand the connection between definite integrals and Riemann sums, and be able to rewrite a definite integral as the limit of a Riemann sum! 🏃
<< Hide Menu
6.3 Riemann Sums, Summation Notation, and Definite Integral Notation
1 min read•june 18, 2024
Emery
Emery
6.3 Riemann Sums, Summation Notation, and Definite Integral Notation
So far in Unit 6, we’ve learned how to approximate the area under the curve. But what if we wanted to find its exact value? For that, we’ll need to learn about integrals and how they are related to the Riemann sum. We’re bringing limits back! 🧠
Σ Summation Notation
Before we get into integrals, we first need to learn how to make taking a Riemann sum faster. To do this, we’ll introduce summation notation so that we can apply algebra instead of manually computing the Riemann sum.
Let’s consider the function over the interval 0 to 5:

Image courtesy of Emery
Now, let’s use a left Riemann sum with 5 subintervals to approximate this area.

Image courtesy of Emery
To convert this to summation notation, we need to create a function that will give us the area of each rectangle. For now, let’s name this function so that gives us the area of the th rectangle. With this function, we can write the Riemann sum as:
Now that we have our summation notation, we need to find an expression for . We know that the area of the rectangle will be , where is the width of the base and is the height.
The width of our base will be constant, and we can find it by dividing the entire interval by the number of subintervals we want:
The height is a little more tricky to notate, but it is just the value of the function at each of the left endpoints. To find this next (or th) point, let’s first find the -value, which we’ll denote as . To do this, we start at 0 and repeatedly add 1, the length of our subinterval.

Image courtesy of Emery
We can write the formula for this -value as or just . We can obtain the -value, or height, by simply plugging in this formula for the -value to our original formula like so: .
We can put these two things together in the area formula as:
which simplifies to
Now, we simply plug that back into our summation notation:
✏️ General Form of Riemann Sum
The general form for the Riemann sum in summation notation is as follows:
for left-endpoint, and
for right-endpoint.
Let’s break down what each symbol means!
- : This denotes the number of subintervals, and is usually given in the problem
- : The lower bound of the interval.
- : The upper bound of the interval.
- : This is the width of each subinterval, and can be calculated by using the formula .
- : This denotes the right endpoint for each rectangle, such that .
- : The original function with plugged in.
- : Tells us to add up the values from for left Riemann sums or for right Riemann sums.
Whew! That’s a lot of pieces to put together. 🧩
∫ Connecting to Definite Integrals
We learned in the last lesson that our Riemann sum becomes more precise if we use more rectangles or a greater value for . But what if we could have infinite rectangles, with infinitely tiny widths?

GIF courtesy of Maplesoft
We see that as , our approximation for the area under the curve gets closer and closer to perfect. This means that we can connect the Riemann sum to the definite integral like so:
Where and .
The truly amazing thing is that this limit tells us the exact value for the definite integral—not just an approximation! 👌
📌 Connecting to Definite Integrals Walkthrough
Let’s connect all the dots and practice converting from summation to definite integral notation with this example problem!
Given the function over the interval , give the summation notation for the right Riemann sum using 10 subintervals and calculate its value. Then, write the definite integral as the limit of the right Riemann sum as approaches infinity.
1) Solving Summation Notation
The first part of the problem asks us to give and solve the summation notation with a fixed, finite . Let’s first write the general form without our area function defined:
Now, we need to define our terms, starting with , which is defined as . Then, we need to define so that we can plug it into the original equation. To get the th right endpoint, we use the formula . In our case, and , so . Now, we plug that back into our original equation to find that . Putting it all together, we find that the right Riemann sum using 10 subintervals is:
The next part of the problem asks us to calculate this sum. This sum essentially tells us to plug in values from 1 to 10 and sum them all up, like so:
This can be rewritten as
Lots of math, but not too bad, right?
2) Writing the Definite Integral
The final part of the problem asks us to write the definite integral as the limit of the right Riemann sum as approaches infinity. First, let’s write the definite integral:
Now, let’s remind ourselves of the general form for equation definite integrals to Riemann sums:
This is where things get a little tricky—since is the variable of our limit, we need to define our other terms in terms of .
- Let’s start by first defining as .
- Then, let’s define in terms of , too. .
- Now let’s plug that back into to find that .
Finally, let’s put that all back into our equation to get:
These problems take a lot of practice, but once you commit the process for finding and to memory, they become very doable. Good luck! 🍀
✏️ Riemann Sum Practice
Try to tackle these three problems yourself! When you’re done, you can check out the solutions and how to walk through them.
❓Practice Problems
- For the function , determine the definite integral as the limit of a Riemann sum.
- Express the definite integral dx as the limit of a Riemann sum.
- The velocity function is given by for the time interval . Express the definite integral as the limit of a Riemann sum.
Answers below! ⬇️
📝 Solutions
Practice Problem 1 Solution
Start by defining in terms of : . Then, do the same for : . Then, plug this in to to get:
Finally, plug this all into the general limit equation to find that:
The next question follows a very similar process.
Practice Problem 2 Solution
You can again start by defining in terms of : . Then, do the same for : . Then, plug this in to to get:
Finally, plug this all into the general limit equation to find that:
Practice Problem 3 Solution
Last question! Start by defining in terms of : . Then, do the same for : . Then, plug this in to to get:
Finally, plug this all into the general limit equation to find that:
💫 Closing
Now that you’ve completed this guide, you should feel comfortable expressing Riemann sums using summation notation, understand the connection between definite integrals and Riemann sums, and be able to rewrite a definite integral as the limit of a Riemann sum! 🏃

© 2025 Fiveable Inc. All rights reserved.