Browse By Unit
7.7 Finding Particular Solutions Using Initial Conditions and Separation of Variables
4 min read•june 18, 2024
7.7 Finding Particular Solutions Using Initial Conditions and Separation of Variables
Welcome to topic 7.7, where you’ll learn about how to find unique solutions to differential equations. You’ve almost made it to the end of the unit! 🌟
In this topic, we’ll learn about the difference between a general solution and a particular solution using separation of variables. To review separation of variables, please look at 7.6 linked here!
🤔 Difference Between General and Particular Solutions
A general solution to a differential equation consists of a constant in the equation. Therefore, when you change the constant, you can get multiple equations when plotting, as seen in the picture below on the left side below. ⬅️ You get a general solution when you don’t have any initial conditions that are given by the problem. When plotting the general solution, you will also get a graph that looks similar to a slope field. For references on slope fields, please look at 7.3 and 7.4!
However, when given an initial condition in the problem, you can solve for a specific equation, which leaves you with one equation on your graph, like on the right side below. ➡️
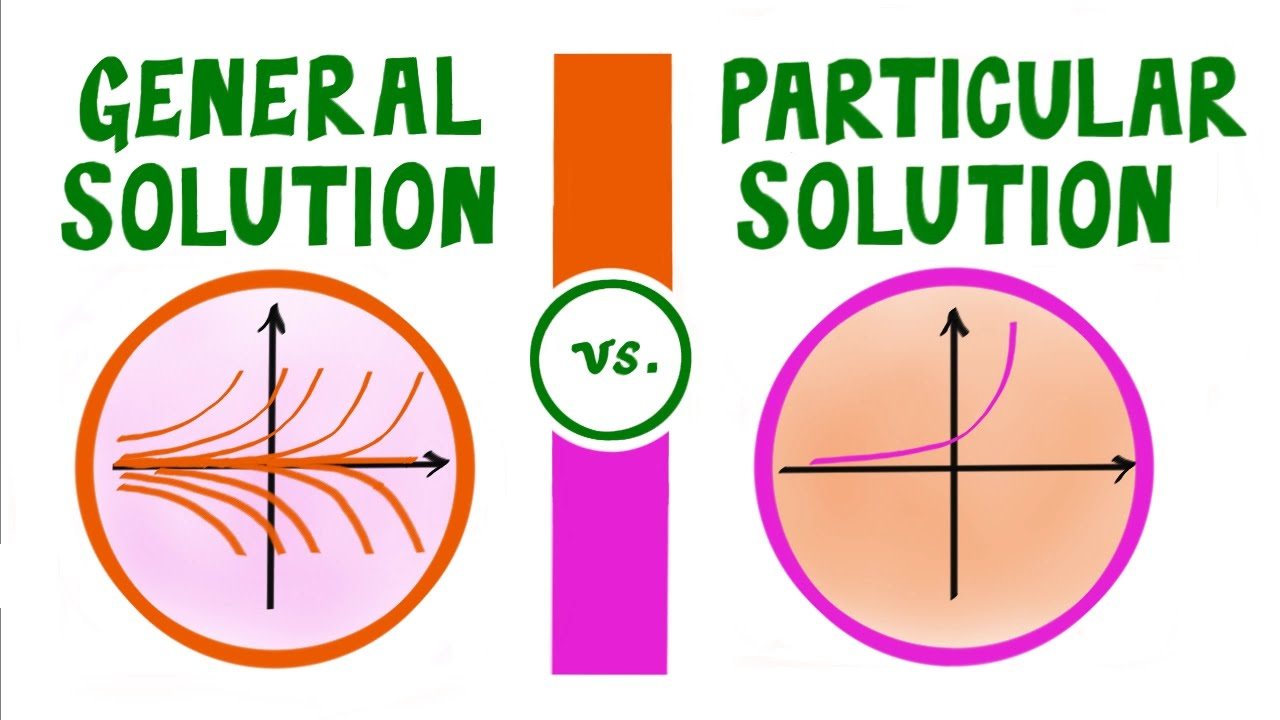
Image Courtesy of Higher Math Notes
Essentially…
- 🎩 A general solution to a differential equation is a family of functions that satisfies the equation. There are infinitely many functions that could do so!
- 🎯 A particular solution is a unique solution that passes through a specific point, and we can calculate it when given initial conditions.
🧠 Particular Solution Function
When this topic shows up on free-response questions and you’re asked to write an expression, you must include the initial condition. Here is a general form that you can use:
This is a particular solution to the differential equation , where (the initial condition!).
Now, let’s get into how to do the math behind finding a particular solution.
🪜 Steps for Solving a Separation of Variables Problem with Initial Conditions
Here are some steps you can follow!
- 🪓 Separate the two variables that you will be using. For example, gather all the ’s on one side and ’s on the other side.
- ◀️ Integrate both sides of the equation with respect to their variables. Make sure not to forget to add the !
- 🟰 Solve for to get the general equation.
- 1️⃣ Plug in your initial conditions (which are given!) for and and solve for .
- 🟰 Finally, plug back in your that you calculated and there’s your particular solution!
This skill combines a lot of skills you already practiced! ✏️
😑 Consideration: Domain Restrictions
Solutions to differential equations may not always be defined for all values of the independent variable. There may be restrictions on the domain, or range of values, for which the solution is valid. These restrictions can arise for several reasons, including: 🔸
- Singularities - Certain values of the independent variable may result in division by zero or other mathematical singularities in the solution, leading to an undefined solution.
- Physical constraints - The solution may only be physically meaningful within certain ranges of the independent variable. For example, the position of a projectile may only be defined when it is above the ground, and not when it is below.
- Mathematical constraints - Certain mathematical conditions may be required for the solution to be well-defined. For example, the solution may only be valid for positive values of the independent variable.
It's important to keep these domain restrictions in mind when solving differential equations and interpreting the results. Ignoring the domain restrictions can lead to incorrect or meaningless solutions. To avoid this, it may be necessary to split the domain into several intervals, each with its own solution, or to use different methods to obtain a solution for different parts of the domain.
Imagine you were asked to find the particular solution of the following differential equation, given the initial condition .
We can see here that there is a domain restriction since the denominator becomes zero when . Therefore, the solution cannot include these values.
📝 AP Free-Response Practice Problem
The following free-response question (FRQ) is from the 2012 AP Calculus AB examination administered by College Board. All credit goes to College Board. We are only going to work on part c since it is the part that focuses on solving differential equations with an initial condition!
The rate at which a baby bird gains weight is proportional to the difference between its adult weight and its current weight. At time , when the bird is first weighed, its weight is 20 grams. If is the weight of the bird, in grams, at time days after it is first weighed, then
Let be the solution to the differential equation above with initial condition .
(c) Use separation of variables to find , the particular solution to the differential equation with initial condition .
Let’s follow the steps we outlined before!
🪓 Step 1) Gather all the ’s on one side and ’s on the other side.
Another possible separation could be moving the to the left side and leaving on the right side!
◀️ Step 2) Integrate both sides of the equation with respect to and .
🟰 Step 3) Add the and solve for the general equation!
Note that this consists of the constant from integrating the left side plus the constant from integrating the right side! Since it is a constant, we can always redefine for the situation!
1️⃣ Step 4) The initial conditions for this problem are for and . Solve for algebraically!
We eliminated the absolute value sign on the left side of the equation because according to the graph that was provided, all the values for were positive for !
🟰 Step 5) Finally, plug back in and solve for !
You already know how to do everything up to step 4 and everything after step 4 is just algebra and arithmetic! You’ve got this with practice! 😃
🔢 Scoring Guidelines Tips
Typically on an FRQ, if there is a differential equation problem, the bulk of the points will come from the part about the differential equation. Here are some important tips to make sure you maximize your points!
1️⃣ Always separate your variables!
Even if you don’t know how to integrate, simply separating your variables can get you one point on the part! If you don’t separate your variables, you lose all the points for that part of the question, even if you do something right later on.
2️⃣ Never forget the !
The constant of integration is incredibly important in differential equation problems because that is how you can use the initial condition to narrow a general solution to a particular solution.
The maximum number of points you can get without the constant is 2: one for separation and one for finding the correct antiderivatives.
📕 Closing
Initially, these types of differential equations will be hard, but with practice and the explicit step-by-step procedure, you can totally rock those questions in the free-response section! You’ve got this! 👏
<< Hide Menu
7.7 Finding Particular Solutions Using Initial Conditions and Separation of Variables
4 min read•june 18, 2024
7.7 Finding Particular Solutions Using Initial Conditions and Separation of Variables
Welcome to topic 7.7, where you’ll learn about how to find unique solutions to differential equations. You’ve almost made it to the end of the unit! 🌟
In this topic, we’ll learn about the difference between a general solution and a particular solution using separation of variables. To review separation of variables, please look at 7.6 linked here!
🤔 Difference Between General and Particular Solutions
A general solution to a differential equation consists of a constant in the equation. Therefore, when you change the constant, you can get multiple equations when plotting, as seen in the picture below on the left side below. ⬅️ You get a general solution when you don’t have any initial conditions that are given by the problem. When plotting the general solution, you will also get a graph that looks similar to a slope field. For references on slope fields, please look at 7.3 and 7.4!
However, when given an initial condition in the problem, you can solve for a specific equation, which leaves you with one equation on your graph, like on the right side below. ➡️

Image Courtesy of Higher Math Notes
Essentially…
- 🎩 A general solution to a differential equation is a family of functions that satisfies the equation. There are infinitely many functions that could do so!
- 🎯 A particular solution is a unique solution that passes through a specific point, and we can calculate it when given initial conditions.
🧠 Particular Solution Function
When this topic shows up on free-response questions and you’re asked to write an expression, you must include the initial condition. Here is a general form that you can use:
This is a particular solution to the differential equation , where (the initial condition!).
Now, let’s get into how to do the math behind finding a particular solution.
🪜 Steps for Solving a Separation of Variables Problem with Initial Conditions
Here are some steps you can follow!
- 🪓 Separate the two variables that you will be using. For example, gather all the ’s on one side and ’s on the other side.
- ◀️ Integrate both sides of the equation with respect to their variables. Make sure not to forget to add the !
- 🟰 Solve for to get the general equation.
- 1️⃣ Plug in your initial conditions (which are given!) for and and solve for .
- 🟰 Finally, plug back in your that you calculated and there’s your particular solution!
This skill combines a lot of skills you already practiced! ✏️
😑 Consideration: Domain Restrictions
Solutions to differential equations may not always be defined for all values of the independent variable. There may be restrictions on the domain, or range of values, for which the solution is valid. These restrictions can arise for several reasons, including: 🔸
- Singularities - Certain values of the independent variable may result in division by zero or other mathematical singularities in the solution, leading to an undefined solution.
- Physical constraints - The solution may only be physically meaningful within certain ranges of the independent variable. For example, the position of a projectile may only be defined when it is above the ground, and not when it is below.
- Mathematical constraints - Certain mathematical conditions may be required for the solution to be well-defined. For example, the solution may only be valid for positive values of the independent variable.
It's important to keep these domain restrictions in mind when solving differential equations and interpreting the results. Ignoring the domain restrictions can lead to incorrect or meaningless solutions. To avoid this, it may be necessary to split the domain into several intervals, each with its own solution, or to use different methods to obtain a solution for different parts of the domain.
Imagine you were asked to find the particular solution of the following differential equation, given the initial condition .
We can see here that there is a domain restriction since the denominator becomes zero when . Therefore, the solution cannot include these values.
📝 AP Free-Response Practice Problem
The following free-response question (FRQ) is from the 2012 AP Calculus AB examination administered by College Board. All credit goes to College Board. We are only going to work on part c since it is the part that focuses on solving differential equations with an initial condition!
The rate at which a baby bird gains weight is proportional to the difference between its adult weight and its current weight. At time , when the bird is first weighed, its weight is 20 grams. If is the weight of the bird, in grams, at time days after it is first weighed, then
Let be the solution to the differential equation above with initial condition .
(c) Use separation of variables to find , the particular solution to the differential equation with initial condition .
Let’s follow the steps we outlined before!
🪓 Step 1) Gather all the ’s on one side and ’s on the other side.
Another possible separation could be moving the to the left side and leaving on the right side!
◀️ Step 2) Integrate both sides of the equation with respect to and .
🟰 Step 3) Add the and solve for the general equation!
Note that this consists of the constant from integrating the left side plus the constant from integrating the right side! Since it is a constant, we can always redefine for the situation!
1️⃣ Step 4) The initial conditions for this problem are for and . Solve for algebraically!
We eliminated the absolute value sign on the left side of the equation because according to the graph that was provided, all the values for were positive for !
🟰 Step 5) Finally, plug back in and solve for !
You already know how to do everything up to step 4 and everything after step 4 is just algebra and arithmetic! You’ve got this with practice! 😃
🔢 Scoring Guidelines Tips
Typically on an FRQ, if there is a differential equation problem, the bulk of the points will come from the part about the differential equation. Here are some important tips to make sure you maximize your points!
1️⃣ Always separate your variables!
Even if you don’t know how to integrate, simply separating your variables can get you one point on the part! If you don’t separate your variables, you lose all the points for that part of the question, even if you do something right later on.
2️⃣ Never forget the !
The constant of integration is incredibly important in differential equation problems because that is how you can use the initial condition to narrow a general solution to a particular solution.
The maximum number of points you can get without the constant is 2: one for separation and one for finding the correct antiderivatives.
📕 Closing
Initially, these types of differential equations will be hard, but with practice and the explicit step-by-step procedure, you can totally rock those questions in the free-response section! You’ve got this! 👏

© 2025 Fiveable Inc. All rights reserved.