Browse By Unit
8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals
4 min read•june 18, 2024
8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals
In this guide, we will look at how to use integrals to find the position, velocity, and acceleration of a function. We'll break it down for you in a way that's not just about numbers and formulas, but about understanding the language of motion. 👟
💭 What are Position, Velocity, and Acceleration?
To begin with, it is important to understand the definitions of position, velocity, and acceleration. Going back to unit 4, we did cover rectilinear motion and applied our knowledge of derivatives to these three concepts. Check out our 4.2 guide here for a review! If you’re curious and want to learn more, we have an entire guide dedicated to these concepts as part of our AP Physics 1 study material.
🧍Position
In the calculus world, position refers to the location of an object in space at a given time. Mathematically, we denote position as a function of time, usually represented by .
Imagine you're in the driver's seat of your dream car, and you want to know where you are on the highway. Well, that's your position . It's like your car's GPS telling you exactly where you are at any given time. Let's say you start at mile marker zero—that's your starting position. We can represent an object’s position as a function of time using a graph, such as the graph below.
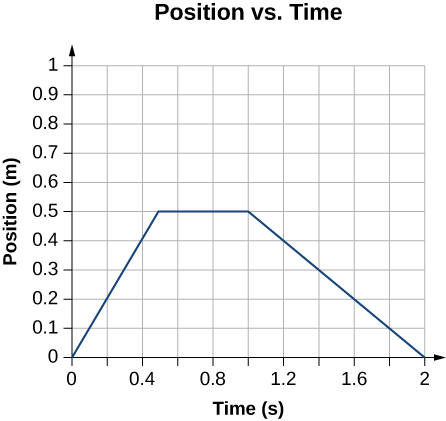
Image courtesy of BCcampus Pressbooks.
Let’s say the graph above represents the movements of a caterpillar. From time to , the caterpillar is moving in a positive direction, away from the starting point. We can conclude this because the slope of the first line segment is positive.
At , the caterpillar is at position 0.5 m—in other words, the caterpillar is 0.5 meters away from its starting point. Then, from to , the caterpillar does not change position, meaning it has stopped moving and is at rest. Whenever there is a horizontal line on a position vs. time graph, it means the object is at rest.
Finally, from to , the caterpillar is moving in the negative direction, back towards the starting point. We can conclude this because the slope of the last line segment is negative.
It is important that you learn to read this graph, as well as the graphs that are pictured below, to make sure you have a good understanding of the relationship between position, velocity, and acceleration. 🤯
🚗 Velocity
Velocity is the rate of change of position concerning time. In simpler terms, it tells us how fast an object is moving and in which direction. Mathematically, velocity, denoted by , is the derivative of the position function with respect to time.
Going back to our example of your dream car, let’s say you step on the gas, and your car starts zooming down the road. How fast are you going, and in which direction? That's velocity, the rate of change of your position. Here is an equation that states the previous sentence in mathematical terms:
As you can see, the velocity can be found by taking the derivative of a position function On a graph, the velocity is the slope of a position vs. time graph, and is often written in m/s (meters per second). We can also use a velocity vs. time graph to represent the velocity of an object as a function of time.

Image courtesy of Study.com.
In the graph above, when the line segment has a positive slope, that means the velocity is steadily increasing. When the segment is horizontal, that means the velocity is constant, but the object is still moving, just with a constant speed. When the line segment has a negative slope, the velocity is steadily decreasing.
There is one more quantity related to velocity: speed. The speed of an object is simply the magnitude of the velocity, or in one-dimensional motion, the absolute value of the velocity.
🏎 Acceleration
Acceleration is the rate of change of the velocity with respect to time. It provides insights into how an object's speed is increasing or decreasing at a given moment. Acceleration is denoted as and is the derivative of velocity with respect to time. It’s like the force that pushes or slows down your car. Speeding up? Positive acceleration. Slamming on the brakes? Negative acceleration (or deceleration). 🚥
Because acceleration is the derivative of the velocity, and velocity is the derivative of position, acceleration can also be defined as the second derivative of position.
In terms of the graphs, the acceleration is the slope of the velocity vs. time graph. In the velocity vs. time graph above, the fact that the line segments are all straight lines, not curves, means the acceleration has constant values. In the first, positively-sloped line segment, the acceleration has a constant positive value. In the horizontal line segment, the velocity is not changing, so the acceleration is zero. In the negatively-sloped line segment, the acceleration has a constant negative value, so the object is decelerating.
✈️ Using Integration to Find Position, Velocity, and Acceleration
Understanding the connections between position, velocity, and acceleration involves integrating and differentiating these functions. Let's explore how integration plays a crucial role in solving real-world problems.
🧮 Integrating Velocity to Find Position
To determine an object's position at any given time, we integrate its velocity function and add the initial position. Recall that the velocity is the derivative of an object’s position, so integrating velocity will give us the position equation of an object. The fundamental theorem of calculus states that the integral of velocity over a specific time interval gives the change in position over that interval.
Here, represents the constant of integration, which corresponds to the initial position. It’s important to recognize here that simply integrating the velocity function gives us the change in position, not the final position of the object. This change in position is called the displacement of the object, defined as the difference between the final position and the initial position .
So, to find the final position of an object, we have to add its initial position after integrating the velocity function. There is one more quantity we can measure by integrating the speed of an object, which is the absolute value of the velocity. This quantity is called the distance traveled, and it measures the length of the path an object takes. Below is an example of how the distance traveled and displacement measure two different quantities.
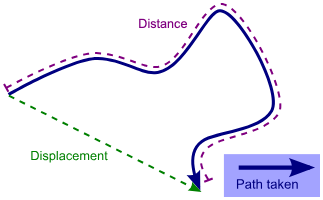
Image courtesy of Khan Academy.
As you can see the displacement only measures the difference between the final and initial positions, but does not take into account that the object may not have taken the shortest path to get there. In the image above, the object took a much longer path to get to the final position, so its distance traveled is greater than its displacement. The general formula for finding the distance traveled is…
where we integrate the absolute value of the velocity function.
🏃 Integrating Acceleration to Find Velocity
Similarly, to find an object's velocity at any time, we integrate its acceleration function. The integral of acceleration with respect to time yields the change in velocity over a given interval.
In this equation, represents the constant of integration, which corresponds to the initial velocity. Just like finding the final position, we need to add the initial velocity to the result of our integral in order to find the final velocity.
✏️ Practice with Examples
❓ Integration and Motion: Question 1
Suppose an object has a velocity function with an initial position . Find the position function .
The velocity function tells us how fast the object is moving at any given time. To find the position function we integrate the velocity function with respect to time. Mathematically, this is represented as…
Integrating this function and adding the initial position, we get…
Great work!
❓ Integration and Motion: Question 2
Given an object's velocity function on the interval with an initial position of , find the displacement and distance traveled.
The displacement is the change in position from to . Mathematically, it's represented as:
Let's integrate the velocity function over the given interval:
Evaluating this expression using the fundamental theorem of calculus yields , which is our displacement. Next, let’s find the distance traveled. The distance traveled is the total path length covered. Since velocity can be negative, we need to consider the absolute value when finding distance.
Integrate the absolute value of the velocity function over the interval. This velocity function is already always positive, so we can remove the absolute value symbols and integrate normally:
Evaluating this integral using the fundamental theorem of calculus yields .
Surprisingly, in this case, the displacement and distance traveled are the same, both equal to . This means that the object didn't take a longer path during the interval , resulting in a positive displacement equal to the distance traveled.
📘 Conclusion
You've successfully navigated through the intricacies of connecting position, velocity, and acceleration using integrals. To recap, the velocity is the derivative of the position with respect to time, and the acceleration is the derivative of velocity with respect to time. The displacement is calculated using the difference between the final and initial position values, and the distance traveled is the length of the path the object took. Here’s a little summary as well:
| Graph Type | Slope Represents | Area Under Graph Represents | Definite Integral Represents | |
| Position | Position vs Time | Velocity | - | - |
| Velocity | Velocity vs Time | Acceleration | Change in position (displacement) | Particle’s displacement over time |
| Acceleration | Acceleration vs Time | Change in acceleration | Change in velocity | - |
Remember, this understanding is not just a tool for calculus exams; it's a powerful skill applicable to various real-world scenarios. Keep practicing, and you'll master the art of solving dynamic problems in no time. 🍀
<< Hide Menu
8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals
4 min read•june 18, 2024
8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals
In this guide, we will look at how to use integrals to find the position, velocity, and acceleration of a function. We'll break it down for you in a way that's not just about numbers and formulas, but about understanding the language of motion. 👟
💭 What are Position, Velocity, and Acceleration?
To begin with, it is important to understand the definitions of position, velocity, and acceleration. Going back to unit 4, we did cover rectilinear motion and applied our knowledge of derivatives to these three concepts. Check out our 4.2 guide here for a review! If you’re curious and want to learn more, we have an entire guide dedicated to these concepts as part of our AP Physics 1 study material.
🧍Position
In the calculus world, position refers to the location of an object in space at a given time. Mathematically, we denote position as a function of time, usually represented by .
Imagine you're in the driver's seat of your dream car, and you want to know where you are on the highway. Well, that's your position . It's like your car's GPS telling you exactly where you are at any given time. Let's say you start at mile marker zero—that's your starting position. We can represent an object’s position as a function of time using a graph, such as the graph below.

Image courtesy of BCcampus Pressbooks.
Let’s say the graph above represents the movements of a caterpillar. From time to , the caterpillar is moving in a positive direction, away from the starting point. We can conclude this because the slope of the first line segment is positive.
At , the caterpillar is at position 0.5 m—in other words, the caterpillar is 0.5 meters away from its starting point. Then, from to , the caterpillar does not change position, meaning it has stopped moving and is at rest. Whenever there is a horizontal line on a position vs. time graph, it means the object is at rest.
Finally, from to , the caterpillar is moving in the negative direction, back towards the starting point. We can conclude this because the slope of the last line segment is negative.
It is important that you learn to read this graph, as well as the graphs that are pictured below, to make sure you have a good understanding of the relationship between position, velocity, and acceleration. 🤯
🚗 Velocity
Velocity is the rate of change of position concerning time. In simpler terms, it tells us how fast an object is moving and in which direction. Mathematically, velocity, denoted by , is the derivative of the position function with respect to time.
Going back to our example of your dream car, let’s say you step on the gas, and your car starts zooming down the road. How fast are you going, and in which direction? That's velocity, the rate of change of your position. Here is an equation that states the previous sentence in mathematical terms:
As you can see, the velocity can be found by taking the derivative of a position function On a graph, the velocity is the slope of a position vs. time graph, and is often written in m/s (meters per second). We can also use a velocity vs. time graph to represent the velocity of an object as a function of time.

Image courtesy of Study.com.
In the graph above, when the line segment has a positive slope, that means the velocity is steadily increasing. When the segment is horizontal, that means the velocity is constant, but the object is still moving, just with a constant speed. When the line segment has a negative slope, the velocity is steadily decreasing.
There is one more quantity related to velocity: speed. The speed of an object is simply the magnitude of the velocity, or in one-dimensional motion, the absolute value of the velocity.
🏎 Acceleration
Acceleration is the rate of change of the velocity with respect to time. It provides insights into how an object's speed is increasing or decreasing at a given moment. Acceleration is denoted as and is the derivative of velocity with respect to time. It’s like the force that pushes or slows down your car. Speeding up? Positive acceleration. Slamming on the brakes? Negative acceleration (or deceleration). 🚥
Because acceleration is the derivative of the velocity, and velocity is the derivative of position, acceleration can also be defined as the second derivative of position.
In terms of the graphs, the acceleration is the slope of the velocity vs. time graph. In the velocity vs. time graph above, the fact that the line segments are all straight lines, not curves, means the acceleration has constant values. In the first, positively-sloped line segment, the acceleration has a constant positive value. In the horizontal line segment, the velocity is not changing, so the acceleration is zero. In the negatively-sloped line segment, the acceleration has a constant negative value, so the object is decelerating.
✈️ Using Integration to Find Position, Velocity, and Acceleration
Understanding the connections between position, velocity, and acceleration involves integrating and differentiating these functions. Let's explore how integration plays a crucial role in solving real-world problems.
🧮 Integrating Velocity to Find Position
To determine an object's position at any given time, we integrate its velocity function and add the initial position. Recall that the velocity is the derivative of an object’s position, so integrating velocity will give us the position equation of an object. The fundamental theorem of calculus states that the integral of velocity over a specific time interval gives the change in position over that interval.
Here, represents the constant of integration, which corresponds to the initial position. It’s important to recognize here that simply integrating the velocity function gives us the change in position, not the final position of the object. This change in position is called the displacement of the object, defined as the difference between the final position and the initial position .
So, to find the final position of an object, we have to add its initial position after integrating the velocity function. There is one more quantity we can measure by integrating the speed of an object, which is the absolute value of the velocity. This quantity is called the distance traveled, and it measures the length of the path an object takes. Below is an example of how the distance traveled and displacement measure two different quantities.

Image courtesy of Khan Academy.
As you can see the displacement only measures the difference between the final and initial positions, but does not take into account that the object may not have taken the shortest path to get there. In the image above, the object took a much longer path to get to the final position, so its distance traveled is greater than its displacement. The general formula for finding the distance traveled is…
where we integrate the absolute value of the velocity function.
🏃 Integrating Acceleration to Find Velocity
Similarly, to find an object's velocity at any time, we integrate its acceleration function. The integral of acceleration with respect to time yields the change in velocity over a given interval.
In this equation, represents the constant of integration, which corresponds to the initial velocity. Just like finding the final position, we need to add the initial velocity to the result of our integral in order to find the final velocity.
✏️ Practice with Examples
❓ Integration and Motion: Question 1
Suppose an object has a velocity function with an initial position . Find the position function .
The velocity function tells us how fast the object is moving at any given time. To find the position function we integrate the velocity function with respect to time. Mathematically, this is represented as…
Integrating this function and adding the initial position, we get…
Great work!
❓ Integration and Motion: Question 2
Given an object's velocity function on the interval with an initial position of , find the displacement and distance traveled.
The displacement is the change in position from to . Mathematically, it's represented as:
Let's integrate the velocity function over the given interval:
Evaluating this expression using the fundamental theorem of calculus yields , which is our displacement. Next, let’s find the distance traveled. The distance traveled is the total path length covered. Since velocity can be negative, we need to consider the absolute value when finding distance.
Integrate the absolute value of the velocity function over the interval. This velocity function is already always positive, so we can remove the absolute value symbols and integrate normally:
Evaluating this integral using the fundamental theorem of calculus yields .
Surprisingly, in this case, the displacement and distance traveled are the same, both equal to . This means that the object didn't take a longer path during the interval , resulting in a positive displacement equal to the distance traveled.
📘 Conclusion
You've successfully navigated through the intricacies of connecting position, velocity, and acceleration using integrals. To recap, the velocity is the derivative of the position with respect to time, and the acceleration is the derivative of velocity with respect to time. The displacement is calculated using the difference between the final and initial position values, and the distance traveled is the length of the path the object took. Here’s a little summary as well:
| Graph Type | Slope Represents | Area Under Graph Represents | Definite Integral Represents | |
| Position | Position vs Time | Velocity | - | - |
| Velocity | Velocity vs Time | Acceleration | Change in position (displacement) | Particle’s displacement over time |
| Acceleration | Acceleration vs Time | Change in acceleration | Change in velocity | - |
Remember, this understanding is not just a tool for calculus exams; it's a powerful skill applicable to various real-world scenarios. Keep practicing, and you'll master the art of solving dynamic problems in no time. 🍀

© 2025 Fiveable Inc. All rights reserved.