Browse By Unit
8.5 Finding the Area Between Curves Expressed as Functions of y
1 min read•june 18, 2024
8.5 Finding the Area Between Curves Expressed as Functions of y
Welcome back to AP Calculus with Fiveable! Today, we're delving into the fascinating world of finding the area between two curves expressed as functions of y. We've already tackled definite integrals and finding the area between two curves, so lets keep up the momentum! 🚀
📏 Area Between Curves defined using
The AP Calculus Exam often throws questions at you that involve finding the area between curves. Most of the time, it will be using functions defined using . To review that process, check out the following Fiveable Guide: Finding the Area Between Curves Expressed as Functions of x. The following image shows the difference between taking the area between curves with vertical slices, as we did in the last key topic, and horizontal slices, as we’ll do today!
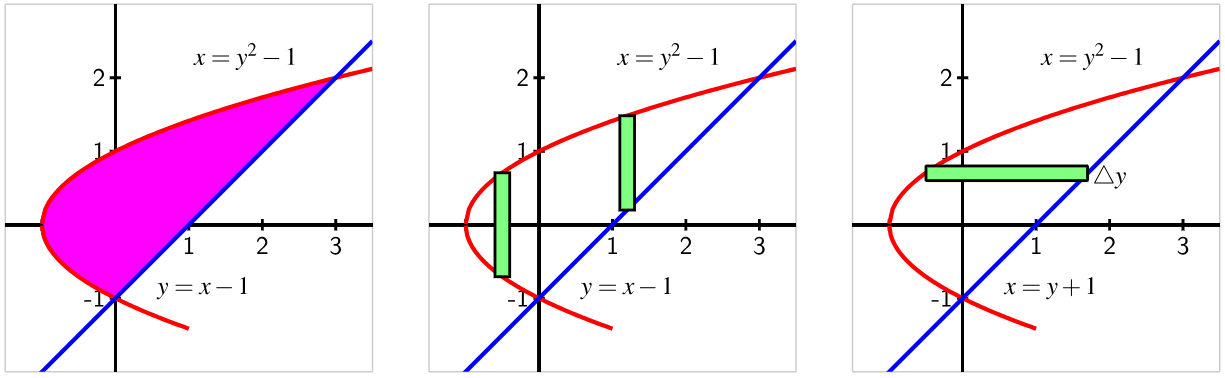
Image Courtesy of Coordinated Calculus
In this case, we're dealing with functions expressed in terms of y. The key idea here is to use horizontal slices to break down the region between the curves into small rectangles. By summing up the areas of these rectangles, we can find the total area. It will be a very similar process to Finding the Area Between Curves Expressed as Functions of x, so lets get right to work!
🧱 Setting Up the Integral
To find the area between two curves and over an interval , we'll be integrating with respect to .
The formula for the area is given by, where :
Here, is the interval on the y-axis where the curves intersect. We take the absolute value to ensure we're dealing with positive areas.
Then you can integrate, making sure it is with respect to . Visually, this is as if we are stacking in the positive and negative directions. Check it out in the graph below:
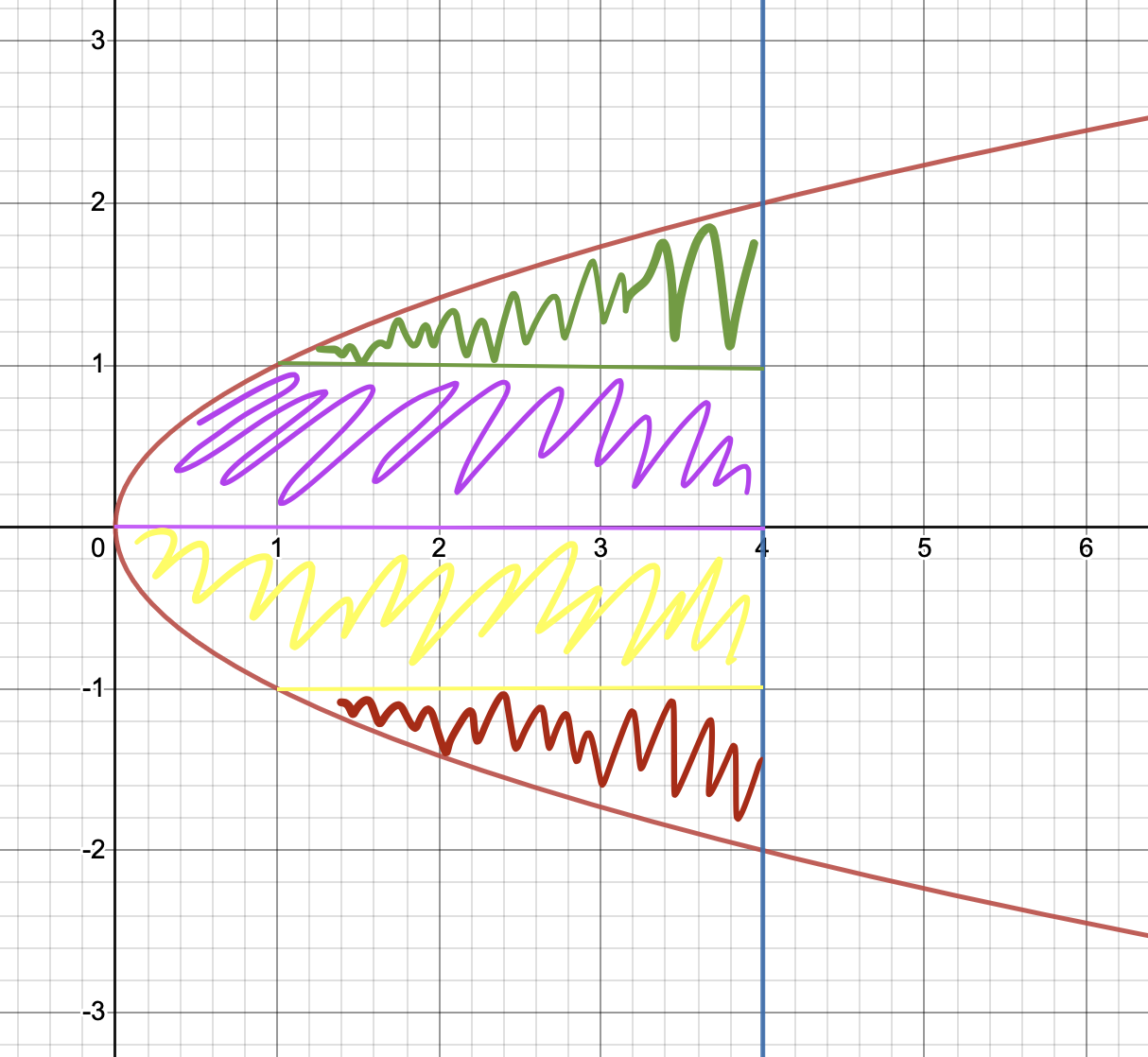
Graph created with Desmos
🧮 Practice Problems
Let’s give some questions a try.
1) Area Between Curves
Given the functions and , find the area between the curves.
Our first step is to identify intersection points. To find where the curves intersect, set : . Solving this equation gives and . So, the interval of integration is .
Visually, the two functions look like this. Make sure to subtract the graphs properly so that the area is positive!
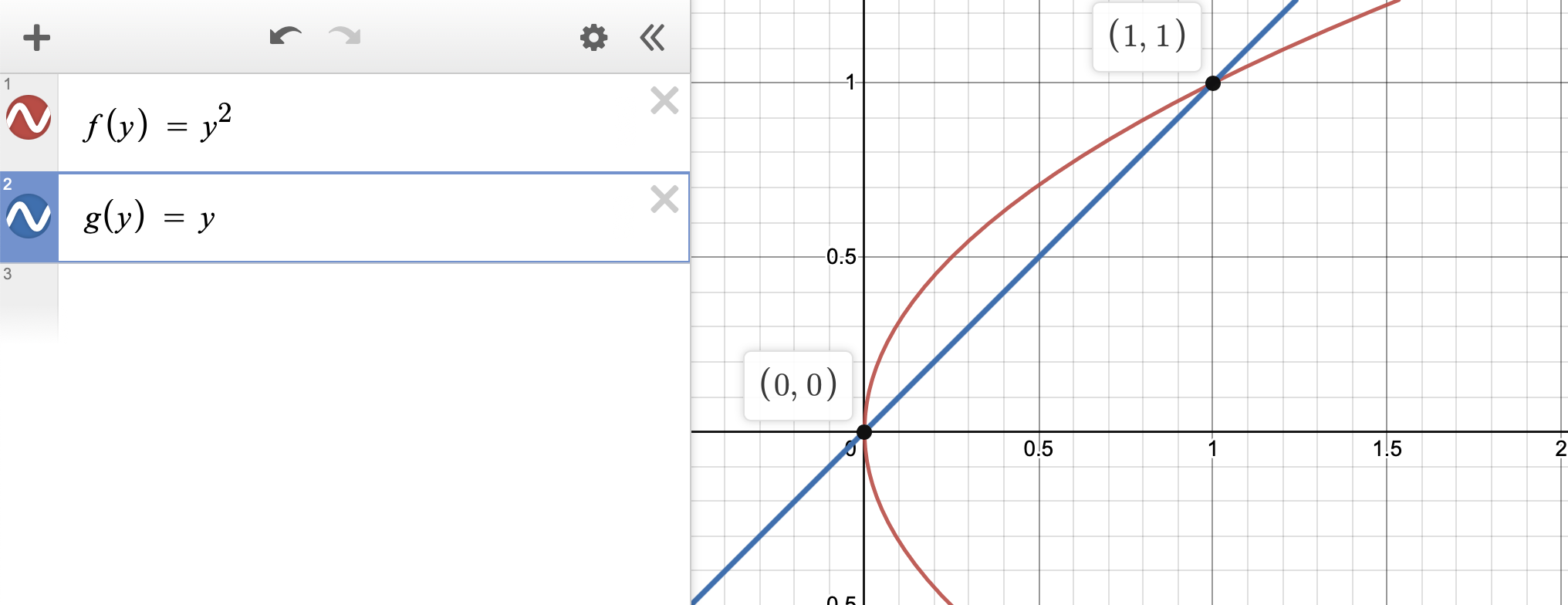
Graph created with Desmos
Next, we need to set up the integral with all of the correct information.
Then, we can evaluate the integral. Make sure you are integrating with respect to !
Our final step is to evaluate at the upper and lower limits, plugging in for y.
Therefore, the area between the curves over the interval is square units. Great work!
2) Area Between Curves using a Calculator
Find the area of the region above the x-axis between and using a calculator.
Depending on which calculator you have, you may be able to plug in more or less information. Let’s go through and set up the problem to be solved in a TI graphing calculator.
First, let’s graph out the functions. This will show us which of the functions has greater -values and can give us the points of intersections.

Graph created with Desmos
Now, we can just plug the following integral into our graphing calculator!
The correct answer is:
Therefore, the area of the region above the x-axis between and is approximately square units.
Amazing job!
🌟 Closing
Great work! You’ve made great strides in mastering integration and finding area between curves, with and without a calculator! You can expect to see these types of problems on the AP Calculus exam in both the Free Response and Multiple Choice sections.
Now, go tackle some more practice problems to solidify your knowledge. Happy studying! 🎉

Image Courtesy of Giphy
<< Hide Menu
8.5 Finding the Area Between Curves Expressed as Functions of y
1 min read•june 18, 2024
8.5 Finding the Area Between Curves Expressed as Functions of y
Welcome back to AP Calculus with Fiveable! Today, we're delving into the fascinating world of finding the area between two curves expressed as functions of y. We've already tackled definite integrals and finding the area between two curves, so lets keep up the momentum! 🚀
📏 Area Between Curves defined using
The AP Calculus Exam often throws questions at you that involve finding the area between curves. Most of the time, it will be using functions defined using . To review that process, check out the following Fiveable Guide: Finding the Area Between Curves Expressed as Functions of x. The following image shows the difference between taking the area between curves with vertical slices, as we did in the last key topic, and horizontal slices, as we’ll do today!

Image Courtesy of Coordinated Calculus
In this case, we're dealing with functions expressed in terms of y. The key idea here is to use horizontal slices to break down the region between the curves into small rectangles. By summing up the areas of these rectangles, we can find the total area. It will be a very similar process to Finding the Area Between Curves Expressed as Functions of x, so lets get right to work!
🧱 Setting Up the Integral
To find the area between two curves and over an interval , we'll be integrating with respect to .
The formula for the area is given by, where :
Here, is the interval on the y-axis where the curves intersect. We take the absolute value to ensure we're dealing with positive areas.
Then you can integrate, making sure it is with respect to . Visually, this is as if we are stacking in the positive and negative directions. Check it out in the graph below:

Graph created with Desmos
🧮 Practice Problems
Let’s give some questions a try.
1) Area Between Curves
Given the functions and , find the area between the curves.
Our first step is to identify intersection points. To find where the curves intersect, set : . Solving this equation gives and . So, the interval of integration is .
Visually, the two functions look like this. Make sure to subtract the graphs properly so that the area is positive!

Graph created with Desmos
Next, we need to set up the integral with all of the correct information.
Then, we can evaluate the integral. Make sure you are integrating with respect to !
Our final step is to evaluate at the upper and lower limits, plugging in for y.
Therefore, the area between the curves over the interval is square units. Great work!
2) Area Between Curves using a Calculator
Find the area of the region above the x-axis between and using a calculator.
Depending on which calculator you have, you may be able to plug in more or less information. Let’s go through and set up the problem to be solved in a TI graphing calculator.
First, let’s graph out the functions. This will show us which of the functions has greater -values and can give us the points of intersections.

Graph created with Desmos
Now, we can just plug the following integral into our graphing calculator!
The correct answer is:
Therefore, the area of the region above the x-axis between and is approximately square units.
Amazing job!
🌟 Closing
Great work! You’ve made great strides in mastering integration and finding area between curves, with and without a calculator! You can expect to see these types of problems on the AP Calculus exam in both the Free Response and Multiple Choice sections.
Now, go tackle some more practice problems to solidify your knowledge. Happy studying! 🎉

Image Courtesy of Giphy

© 2025 Fiveable Inc. All rights reserved.