Browse By Unit
8.1 Finding the Average Value of a Function on an Interval
2 min read•june 18, 2024
Anusha Tekumulla
Jesse
Anusha Tekumulla
Jesse
8.1 Finding the Average Value of a Function on an Interval
Welcome back to AP Calculus with Fiveable! This topic focuses on finding the average value of a continuous function using definite integrals.
🔢 Average Value of a Function
The average value of a function will allow us to solve problems that involve the accumulation of change over an interval, which will later be used to understand more difficult topics of integration.
For questions that require the average value of a function, we are never given a finite number of data points. Therefore, we must use integration to determine what the average value is.
This idea is fairly simple once you memorize a key piece of information: if f is continuous on then the average value of f on ] is the following.
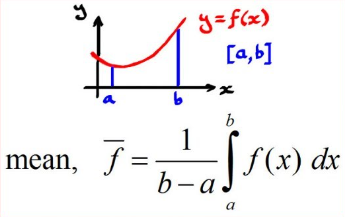
Image Courtesy of ExamSolutions
🔍Average Value of a Function Steps
Here are some steps to help break down the formula!
- Set up the integral so that you integrate f(x) from a to b with respect to x, which will calculate the area under the curve between these two limits.
- Then place the fraction in front of the integral, which is simply the reciprocal of the difference between a and b.
- Evaluating this expression allows you to get the average y-value of this function between
✏️ Average Value of a Function Walkthrough
If the formula still seems a little difficult to understand due to its notation, practice questions are the best way to better understand its use!
Consider the function on the interval [1,4]. Find the average value of this function on the interval.
In this case, a = 1 and b = 4. So we begin by subbing the 1 and 4 into both the denominator of the fraction in front of the integral and the limits of the integral.
Next, take the integral of f(x).
Finally, we can sub in the limits and evaluate.
Time for you to practice some questions yourself! ⬇️
📝 Average Value of a Function Practice Problems
Give each of these problems a try before you move onto the solutions!
- What is the average value of on the interval ?
- What is the average value of on the interval ?
- What is the average value of on the interval ?
Average Value of a Function Question Solutions
Question 1 Solution
Question 2 Solution
Question 3 Solution
⭐ Closing
Great job! This topic often shows up as part (a) of FRQs, so keep this in mind for the AP.
<< Hide Menu
8.1 Finding the Average Value of a Function on an Interval
2 min read•june 18, 2024
Anusha Tekumulla
Jesse
Anusha Tekumulla
Jesse
8.1 Finding the Average Value of a Function on an Interval
Welcome back to AP Calculus with Fiveable! This topic focuses on finding the average value of a continuous function using definite integrals.
🔢 Average Value of a Function
The average value of a function will allow us to solve problems that involve the accumulation of change over an interval, which will later be used to understand more difficult topics of integration.
For questions that require the average value of a function, we are never given a finite number of data points. Therefore, we must use integration to determine what the average value is.
This idea is fairly simple once you memorize a key piece of information: if f is continuous on then the average value of f on ] is the following.

Image Courtesy of ExamSolutions
🔍Average Value of a Function Steps
Here are some steps to help break down the formula!
- Set up the integral so that you integrate f(x) from a to b with respect to x, which will calculate the area under the curve between these two limits.
- Then place the fraction in front of the integral, which is simply the reciprocal of the difference between a and b.
- Evaluating this expression allows you to get the average y-value of this function between
✏️ Average Value of a Function Walkthrough
If the formula still seems a little difficult to understand due to its notation, practice questions are the best way to better understand its use!
Consider the function on the interval [1,4]. Find the average value of this function on the interval.
In this case, a = 1 and b = 4. So we begin by subbing the 1 and 4 into both the denominator of the fraction in front of the integral and the limits of the integral.
Next, take the integral of f(x).
Finally, we can sub in the limits and evaluate.
Time for you to practice some questions yourself! ⬇️
📝 Average Value of a Function Practice Problems
Give each of these problems a try before you move onto the solutions!
- What is the average value of on the interval ?
- What is the average value of on the interval ?
- What is the average value of on the interval ?
Average Value of a Function Question Solutions
Question 1 Solution
Question 2 Solution
Question 3 Solution
⭐ Closing
Great job! This topic often shows up as part (a) of FRQs, so keep this in mind for the AP.

© 2025 Fiveable Inc. All rights reserved.