Browse By Unit
8.3 Using Accumulation Functions and Definite Integrals in Applied Contexts
4 min read•june 18, 2024
8.3 Using Accumulation Functions and Definite Integrals in Applied Contexts
Welcome to the third topic in Unit 8! In this key topic, we’ll be learning more about what an accumulation problem is and how to solve one. For a more in-depth review of how to take an integral, take a look at Unit 6!
⛰️ Accumulation Problems
So before we learn how to solve an accumulation problem, we need to know what an accumulation problem is in the first place. The picture below is a visual representation of the graphical meaning of an integral. 📈
To calculate the integral of a function, you are essentially taking the area that is under the curve! More specifically in an accumulation problem, you are taking the integral of the rate of change function that you are given.
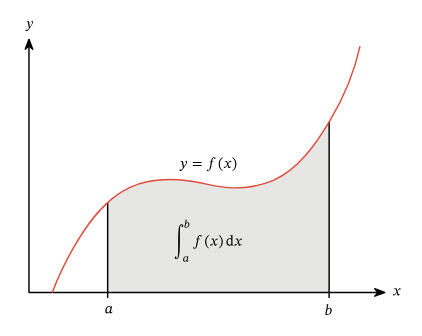
Image Courtesy of Nagwa
📝 Walkthrough of an Accumulation Problem
This will be a very simple example to understand the concept of accumulation. You are given a velocity equation, which is . How would you calculate the total displacement between and ?
Here’s one way we can solve the problem, step by step.
1️⃣ Identify the rate of change function.
In this case, the rate of change function is velocity since we want to end up with time! ⏲️
2️⃣ Set up the definite integral to evaluate.
Why exactly is this the definite integral? Good question! 😄
The definition of velocity is the rate of change of the position. Since we are trying to find the displacement, it makes sense that we are taking the integral of the velocity.
3️⃣ Evaluate the integral!
We get that the final displacement is !
📝 2004 AP Calculus AB Form B Question 2c Walkthrough
The following free-response question (FRQ) is from the 2004 AP Calculus AB examination from Form B administered by College Board. All credit to College Board.

Image Courtesy of College Board
For this problem, we are only working on Part C because that is the part that has to do with accumulation. ✨
🪜Accumulation Function: Steps to Follow
1️⃣ Identify the rate of change function.
2️⃣ Set up the definite integral to find the net change.
3️⃣ Evaluate the integral.
4️⃣ Use any provided initial condition to complete the problem!
🔎 Step 1: Identifying the rate of change function
The function is given in the problem. Here it is below! Remember that the units for the rate of change is mosquitoes per day 🦟!
📕 Steps 2 & 3: Setting up and evaluating the definite integral
In Part C, we’re trying to find the number of mosquitoes on the island at , which means we are trying to find the accumulation of the rate of change from to !
✅ Step 4: Using the initial condition
In the problem you are told that at , there are mosquitoes on the island. Since we calculated the total change, we can add that to our initial condition to get the final answer!
Since the final answer says to round to the nearest whole number, the final answer will be 964 mosquitoes! 🦟
⭐️ Closing
Congrats on making it through the application part of the accumulation problems. With continuous practice, you’ll learn more and be able to ace the AP Calculus exam! You’ve got this! ☺️
<< Hide Menu
8.3 Using Accumulation Functions and Definite Integrals in Applied Contexts
4 min read•june 18, 2024
8.3 Using Accumulation Functions and Definite Integrals in Applied Contexts
Welcome to the third topic in Unit 8! In this key topic, we’ll be learning more about what an accumulation problem is and how to solve one. For a more in-depth review of how to take an integral, take a look at Unit 6!
⛰️ Accumulation Problems
So before we learn how to solve an accumulation problem, we need to know what an accumulation problem is in the first place. The picture below is a visual representation of the graphical meaning of an integral. 📈
To calculate the integral of a function, you are essentially taking the area that is under the curve! More specifically in an accumulation problem, you are taking the integral of the rate of change function that you are given.

Image Courtesy of Nagwa
📝 Walkthrough of an Accumulation Problem
This will be a very simple example to understand the concept of accumulation. You are given a velocity equation, which is . How would you calculate the total displacement between and ?
Here’s one way we can solve the problem, step by step.
1️⃣ Identify the rate of change function.
In this case, the rate of change function is velocity since we want to end up with time! ⏲️
2️⃣ Set up the definite integral to evaluate.
Why exactly is this the definite integral? Good question! 😄
The definition of velocity is the rate of change of the position. Since we are trying to find the displacement, it makes sense that we are taking the integral of the velocity.
3️⃣ Evaluate the integral!
We get that the final displacement is !
📝 2004 AP Calculus AB Form B Question 2c Walkthrough
The following free-response question (FRQ) is from the 2004 AP Calculus AB examination from Form B administered by College Board. All credit to College Board.

Image Courtesy of College Board
For this problem, we are only working on Part C because that is the part that has to do with accumulation. ✨
🪜Accumulation Function: Steps to Follow
1️⃣ Identify the rate of change function.
2️⃣ Set up the definite integral to find the net change.
3️⃣ Evaluate the integral.
4️⃣ Use any provided initial condition to complete the problem!
🔎 Step 1: Identifying the rate of change function
The function is given in the problem. Here it is below! Remember that the units for the rate of change is mosquitoes per day 🦟!
📕 Steps 2 & 3: Setting up and evaluating the definite integral
In Part C, we’re trying to find the number of mosquitoes on the island at , which means we are trying to find the accumulation of the rate of change from to !
✅ Step 4: Using the initial condition
In the problem you are told that at , there are mosquitoes on the island. Since we calculated the total change, we can add that to our initial condition to get the final answer!
Since the final answer says to round to the nearest whole number, the final answer will be 964 mosquitoes! 🦟
⭐️ Closing
Congrats on making it through the application part of the accumulation problems. With continuous practice, you’ll learn more and be able to ace the AP Calculus exam! You’ve got this! ☺️

© 2025 Fiveable Inc. All rights reserved.