Browse By Unit
8.9 Volume with Disc Method: Revolving Around the x- or y-Axis
5 min read•june 18, 2024
8.9 Volume with Disc Method: Revolving Around the x- or y-Axis
In AP Calculus, we dive deep into the concept of calculating volume through the disc method, where we revolve shapes around either the x- or y-axis. This method is fundamental in solving problems involving volumes of solids of revolution. Let’s get started!
🌪️ Volumes of Solids of Revolution
When we talk about finding the volume of a solid of revolution, we're essentially determining how much space the 3D shape occupies. To do this, we take a curve and rotate it around a particular axis, which creates a solid shape. The disc method allows us to calculate the volume of these solids accurately.
🥏 The Disc Method: X-Axis
The disc method involves slicing the solid into infinitely thin discs perpendicular to the axis of rotation. By summing up the volumes of these discs using definite integrals, we obtain the total volume of the solid.
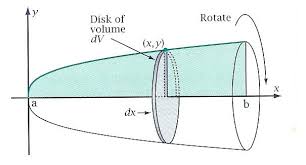
Courtesy of Cochran Math
To find the volume of a solid rotated around the x-axis, as shown above, we add together the volume of many thin cross-sections! These cross sections of the rotate volume have a width of (or approaching 0) and a radius of . As shown above, each cross-section is a super flat cylinder, with a volume of , where is the width and is the radius. Plugging in our formulas for width and radius, we get:
To add many of these volumes together, we use an integral! Our final integral is:
Where and are the stated boundaries or endpoints for the given equation , given as and .
🥏 The Disc Method: Y-Axis
Sometimes, you will be asked to rotate an object around the y-axis.
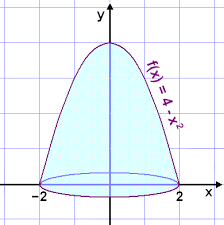
Courtesy of MathScene
The process is pretty much the same, except you replace and with and . The new equation to use is:
Where the boundaries and are given as and .
✏️ Solving Using the Disc Method
To solve any rotated solid problem involving the x- or y-axis and only 1 equation, use these steps!
- 🧠 Determine the Axis: Identify whether the solid is being revolved around the x-axis or y-axis. This determines how we set up our integral.
- ⛏️ Slice the Solid: Visualize slicing the solid into thin discs perpendicular to the chosen axis. Each disc represents an infinitesimally small volume element.
- 🧱 Setup Integral: Using definite integrals, set up the integral to sum up the volumes of all these discs along the given interval. Use the equation above!
- 📏 Evaluate the Integral: Once the integral is set up, evaluate it to find the total volume of the solid.
🌶️ Practicing with the Disc Method
Let’s get into how to apply these steps to practice problems!
✏️ Disc Method: Practice Question 1
Calculate the volume of the solid obtained by revolving the region bounded by the curves , , and the y-axis about the x-axis.
🧠 Step 1) Determine the Axis
As stated in the question, we need to find the volume of the solid obtained by revolving the region bounded by the curves about the x-axis.
⛏️ Step 2) Slice the Solid
Visualize slicing the region into thin discs perpendicular to the x-axis. At this point, you should be graphing all of your equations and shading the area to be revolved!
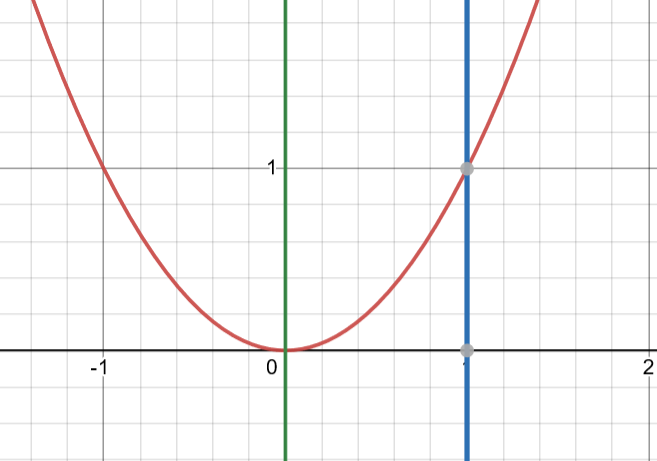
Graph Courtesy of Julianna Fontanilla
🧱 Step 3) Setup Integral
Since we're revolving around the x-axis, we integrate with respect to x and use the first general equation. The volume can be found using the formula below where represents the function defining the region and and represent the interval of integration.
📏 Step 4) Evaluate the Integral
Integrate the function from to using definite integration. As you can see on the graph, the lower bound of this integral occur first where the function intersects with the y-axis, or when . The upper bound occurs when .
Amazing work! Let’s give another one a try.
✏️ Disc Method: Practice Question 2
Find the area of the solid found by rotating the region bounded by , , and around the y-axis.
🧠 Step 1) Determine the Axis
The problem states that we are rotating around the y-axis. This means that our integral should be in terms of instead of .
⛏️ Step 2) Slice the Solid
Again, we need to draw out the integral!
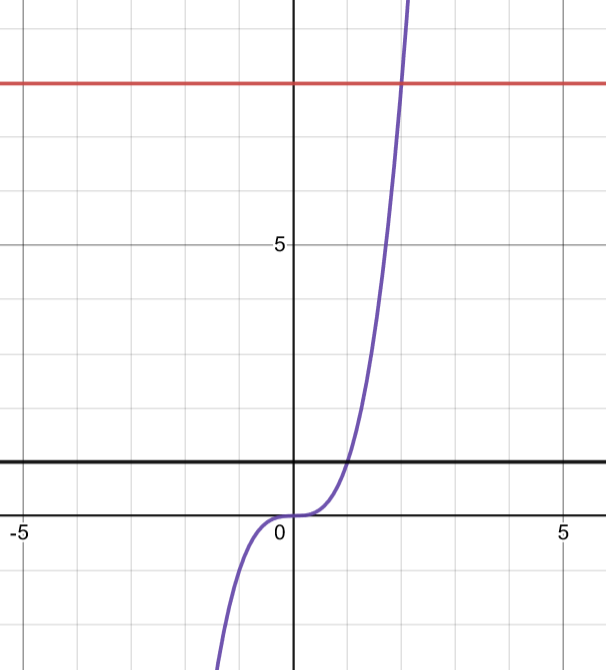
Graph Courtesy of Julianna Fontanilla
As you can see here, we are rotating the area between the purple function and the y-axis which is also between the red and black horizontal lines of and respectively.
🧱 Step 3) Setup Integral
Be careful here! Remember that for rotating around the y-axis, you need to have your main function to rotate in terms of , or look like . Our current equation given is:
To change this to terms of , we would take the cube root of both sides to get:
This is the correct function to use in your general integral formula!
📏 Step 4) Evaluate the Integral
Again, the general integral format is
We are told that our bounds are , , and . Plugging this information into the equation, we get:
This simplifies to…
You did it! 👏
📒 Conclusion
Mastering the disc method for finding volumes of solids of revolution expands our problem-solving toolkit in calculus. Let’s move on to the next guide for wider applications of this important technique!
<< Hide Menu
8.9 Volume with Disc Method: Revolving Around the x- or y-Axis
5 min read•june 18, 2024
8.9 Volume with Disc Method: Revolving Around the x- or y-Axis
In AP Calculus, we dive deep into the concept of calculating volume through the disc method, where we revolve shapes around either the x- or y-axis. This method is fundamental in solving problems involving volumes of solids of revolution. Let’s get started!
🌪️ Volumes of Solids of Revolution
When we talk about finding the volume of a solid of revolution, we're essentially determining how much space the 3D shape occupies. To do this, we take a curve and rotate it around a particular axis, which creates a solid shape. The disc method allows us to calculate the volume of these solids accurately.
🥏 The Disc Method: X-Axis
The disc method involves slicing the solid into infinitely thin discs perpendicular to the axis of rotation. By summing up the volumes of these discs using definite integrals, we obtain the total volume of the solid.

Courtesy of Cochran Math
To find the volume of a solid rotated around the x-axis, as shown above, we add together the volume of many thin cross-sections! These cross sections of the rotate volume have a width of (or approaching 0) and a radius of . As shown above, each cross-section is a super flat cylinder, with a volume of , where is the width and is the radius. Plugging in our formulas for width and radius, we get:
To add many of these volumes together, we use an integral! Our final integral is:
Where and are the stated boundaries or endpoints for the given equation , given as and .
🥏 The Disc Method: Y-Axis
Sometimes, you will be asked to rotate an object around the y-axis.

Courtesy of MathScene
The process is pretty much the same, except you replace and with and . The new equation to use is:
Where the boundaries and are given as and .
✏️ Solving Using the Disc Method
To solve any rotated solid problem involving the x- or y-axis and only 1 equation, use these steps!
- 🧠 Determine the Axis: Identify whether the solid is being revolved around the x-axis or y-axis. This determines how we set up our integral.
- ⛏️ Slice the Solid: Visualize slicing the solid into thin discs perpendicular to the chosen axis. Each disc represents an infinitesimally small volume element.
- 🧱 Setup Integral: Using definite integrals, set up the integral to sum up the volumes of all these discs along the given interval. Use the equation above!
- 📏 Evaluate the Integral: Once the integral is set up, evaluate it to find the total volume of the solid.
🌶️ Practicing with the Disc Method
Let’s get into how to apply these steps to practice problems!
✏️ Disc Method: Practice Question 1
Calculate the volume of the solid obtained by revolving the region bounded by the curves , , and the y-axis about the x-axis.
🧠 Step 1) Determine the Axis
As stated in the question, we need to find the volume of the solid obtained by revolving the region bounded by the curves about the x-axis.
⛏️ Step 2) Slice the Solid
Visualize slicing the region into thin discs perpendicular to the x-axis. At this point, you should be graphing all of your equations and shading the area to be revolved!

Graph Courtesy of Julianna Fontanilla
🧱 Step 3) Setup Integral
Since we're revolving around the x-axis, we integrate with respect to x and use the first general equation. The volume can be found using the formula below where represents the function defining the region and and represent the interval of integration.
📏 Step 4) Evaluate the Integral
Integrate the function from to using definite integration. As you can see on the graph, the lower bound of this integral occur first where the function intersects with the y-axis, or when . The upper bound occurs when .
Amazing work! Let’s give another one a try.
✏️ Disc Method: Practice Question 2
Find the area of the solid found by rotating the region bounded by , , and around the y-axis.
🧠 Step 1) Determine the Axis
The problem states that we are rotating around the y-axis. This means that our integral should be in terms of instead of .
⛏️ Step 2) Slice the Solid
Again, we need to draw out the integral!

Graph Courtesy of Julianna Fontanilla
As you can see here, we are rotating the area between the purple function and the y-axis which is also between the red and black horizontal lines of and respectively.
🧱 Step 3) Setup Integral
Be careful here! Remember that for rotating around the y-axis, you need to have your main function to rotate in terms of , or look like . Our current equation given is:
To change this to terms of , we would take the cube root of both sides to get:
This is the correct function to use in your general integral formula!
📏 Step 4) Evaluate the Integral
Again, the general integral format is
We are told that our bounds are , , and . Plugging this information into the equation, we get:
This simplifies to…
You did it! 👏
📒 Conclusion
Mastering the disc method for finding volumes of solids of revolution expands our problem-solving toolkit in calculus. Let’s move on to the next guide for wider applications of this important technique!

© 2025 Fiveable Inc. All rights reserved.