Browse By Unit
8.12 Volume with Washer Method: Revolving Around Other Axes
4 min read•june 18, 2024
8.12 Volume with Washer Method: Revolving Around Other Axes
🎉 Hello, hello! Welcome to 8.12, the last section of Unit 8 AB Calculus.
This section is about using the washer method plus revolving around other axes. It requires a couple of skills acquired earlier in this unit! If you need a refresher, check out the following guides:
- 8.10 Volume with Disc Method: Revolving Around Other Axes
- 8.11 Volume with Washer Method: Revolving Around the x- or y-Axis
Let’s get into it!
🌪️ Revolving Around Other Axes
Revolving around other axes just means that you choose a different vertical or horizontal line of either x = a or y =b to revolve around instead of the x or y axis.
Just as a reminder, the general equation looks like this for revolving around a horizontal line of .
Or, it can look like the following for revolving around a vertical line of .
🧼 Washer Method
The washer method removes the area of a circle of a small radius from the area of a circle with a bigger radius, creating a washer shape (like the construction component).
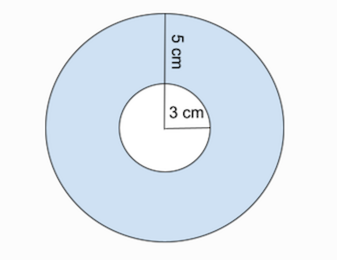
Image courtesy of study.com.
The general formula for the integral using the washer method is
↪️ The Washer Method Around Other Axes
Taking aspects from both of the general integrals above, we get the new integral of…
This is the complete washer integral used with revolving around other axes! You aren’t given a formula sheet on the AP Calculus Exam, so it would be a good idea to memorize this.
✏️ The Washer Method: Practice Time!
Let’s apply this integral to some practice questions.
📝 The Washer Method Practice Question
Find the volume of the solid found by revolving the area between and about the line .
First off, always start by graphing all given functions!
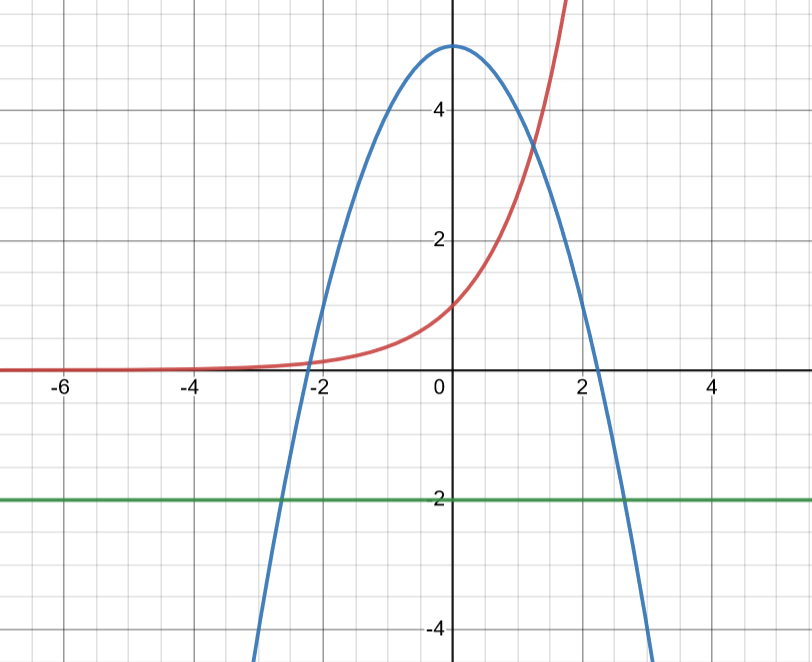
Graph created with Desmos.
As you see in this image, is farther from the green axis of rotation than so it should come first in the washer integral.
Next, we need to find our lower and upper bounds, which occur where the 2 functions intersect. This happens when which can be found using a graphing calculator. The 2 intersections are approximately at and which are the lower and upper bounds respectively. We also know that since ,
Now, it’s time to use the general equation! Plugging in all of our known information,
becomes
After using FOIL, the integral becomes
This integral can be solved with the integral power rule, basic rules about sums of integrals, and u-substitution. For more information on solving integrals, check out our guide here!
Back to the problem! We get
Solving this with a calculator, we get a final volume of 275.7.
📝 The Washer Method AP Practice Question
Let’s try a real AP problem involving revolution of a solid! Note that we will only be solving part (b) of this free-response question.
The following free-response question (FRQ) is from the 2016 AP Calculus AB examination administered by College Board. All credit to College Board.
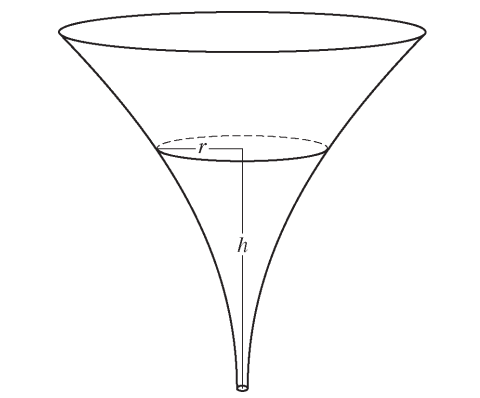
All credit to College Board, 2016 AP, FRQ #5.
The inside of a funnel of height 10 inches has circular cross sections, as shown in the figure above. At height , the radius of the funnel is given by , where . The units of and are inches.
Find the volume of the funnel.
This problem states that the radius of the funnel is and that the bounds of this funnel are , where h is the height in inches. Remember that the original washer equation is
Which is simply the integral of the area of the solid at all possible points, which can be represented by
where pi is the radius.
Here, we are told that the radius is so we can just substitute this into the above equation!
Our final integral to solve is
which can be simplified to
or
When solving this integral, we get
This is equal to , our final answer.
⭐ Closing
To succeed at rotated volume problems, remember to draw or graph all of the given functions, find your upper and lower bounds, and be careful with negative numbers. With such a complicated process, it is very important to check your work if you have the time. And as always, practice, practice, practice. You can do this! 🍀
<< Hide Menu
8.12 Volume with Washer Method: Revolving Around Other Axes
4 min read•june 18, 2024
8.12 Volume with Washer Method: Revolving Around Other Axes
🎉 Hello, hello! Welcome to 8.12, the last section of Unit 8 AB Calculus.
This section is about using the washer method plus revolving around other axes. It requires a couple of skills acquired earlier in this unit! If you need a refresher, check out the following guides:
- 8.10 Volume with Disc Method: Revolving Around Other Axes
- 8.11 Volume with Washer Method: Revolving Around the x- or y-Axis
Let’s get into it!
🌪️ Revolving Around Other Axes
Revolving around other axes just means that you choose a different vertical or horizontal line of either x = a or y =b to revolve around instead of the x or y axis.
Just as a reminder, the general equation looks like this for revolving around a horizontal line of .
Or, it can look like the following for revolving around a vertical line of .
🧼 Washer Method
The washer method removes the area of a circle of a small radius from the area of a circle with a bigger radius, creating a washer shape (like the construction component).

Image courtesy of study.com.
The general formula for the integral using the washer method is
↪️ The Washer Method Around Other Axes
Taking aspects from both of the general integrals above, we get the new integral of…
This is the complete washer integral used with revolving around other axes! You aren’t given a formula sheet on the AP Calculus Exam, so it would be a good idea to memorize this.
✏️ The Washer Method: Practice Time!
Let’s apply this integral to some practice questions.
📝 The Washer Method Practice Question
Find the volume of the solid found by revolving the area between and about the line .
First off, always start by graphing all given functions!

Graph created with Desmos.
As you see in this image, is farther from the green axis of rotation than so it should come first in the washer integral.
Next, we need to find our lower and upper bounds, which occur where the 2 functions intersect. This happens when which can be found using a graphing calculator. The 2 intersections are approximately at and which are the lower and upper bounds respectively. We also know that since ,
Now, it’s time to use the general equation! Plugging in all of our known information,
becomes
After using FOIL, the integral becomes
This integral can be solved with the integral power rule, basic rules about sums of integrals, and u-substitution. For more information on solving integrals, check out our guide here!
Back to the problem! We get
Solving this with a calculator, we get a final volume of 275.7.
📝 The Washer Method AP Practice Question
Let’s try a real AP problem involving revolution of a solid! Note that we will only be solving part (b) of this free-response question.
The following free-response question (FRQ) is from the 2016 AP Calculus AB examination administered by College Board. All credit to College Board.

All credit to College Board, 2016 AP, FRQ #5.
The inside of a funnel of height 10 inches has circular cross sections, as shown in the figure above. At height , the radius of the funnel is given by , where . The units of and are inches.
Find the volume of the funnel.
This problem states that the radius of the funnel is and that the bounds of this funnel are , where h is the height in inches. Remember that the original washer equation is
Which is simply the integral of the area of the solid at all possible points, which can be represented by
where pi is the radius.
Here, we are told that the radius is so we can just substitute this into the above equation!
Our final integral to solve is
which can be simplified to
or
When solving this integral, we get
This is equal to , our final answer.
⭐ Closing
To succeed at rotated volume problems, remember to draw or graph all of the given functions, find your upper and lower bounds, and be careful with negative numbers. With such a complicated process, it is very important to check your work if you have the time. And as always, practice, practice, practice. You can do this! 🍀

© 2025 Fiveable Inc. All rights reserved.