Browse By Unit
9.3 Finding Arc Lengths of Curves Given by Parametric Equations
5 min read•june 18, 2024
9.3 Finding Arc Lengths of Curves Given by Parametric Equations
For this portion of the AP Calculus BC course, we will learn how to apply what we have previously learned about arc length to parametric curves. To learn more about finding arc lengths of smooth planar curves, please refer to the Unit 8.13 study guide!
🏹 Reviewing Arc Length
In calculus, the arc length of a curve refers to the distance between two points on a curve. For example, if we were to mark two points on a paperclip, we could measure the arc length between those two points by unraveling the paperclip. Once the paperclip is straightened out, we can use a ruler to measure the distance between those two points. A similar strategy is used to measure the arc length of a curve.
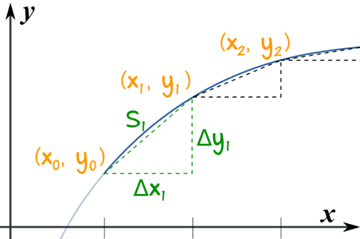
Image Courtesy of Math Is Fun
✏️ Derivation of Arc Length Formula (Cartesian)
This image above depicts how calculus can be used to calculate the arc length of curves. The process essentially involves using the Pythagorean Theorem, , to find the hypotenuse of a triangle with side lengths of and . By adding up all the little hypotenuses, we can get a good approximation for the arc length of the curve. The arc length formula is derived from this idea. The derivation is shown in greater detail below:
However, this formula is only used to find the arc length of smooth planar curves. We need to adapt the formula a little more in order to use it for parametric curves!
💭 Arc Length of Parametric Curves
Review of Parametric Equations
To understand how the arc length formula needs to be adapted for parametric equations, it’s important that you first understand the relationship between parametric and Cartesian equations. The diagram below does a great job of helping us visualize this relationship!
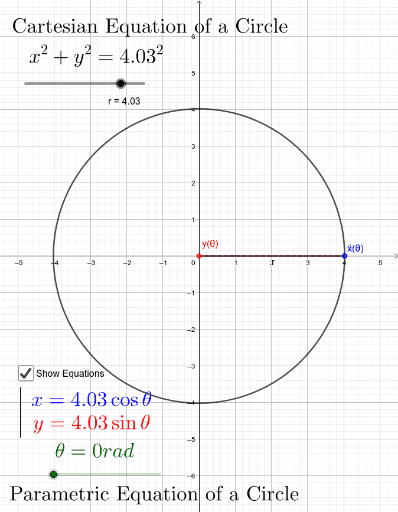
Image Courtesy of GeoGebra
As can be seen in the image, while .
✏️ Deriving the Arc Length Formula (Parametric)
Earlier, we derived the arc length formula for cartesian curves. When we substitute for for their parametric equivalents, and , we arrive at the arc length formula for parametric curves. This process is shown below:
Notice that the formula looks similar to the case of the Cartesian equation. However, both x and y are changing, so we need to account for both of their fluctuations!
📝 Arc Length—Parametric Practice
Now that we know the formula for finding the arc length of parametric curves, let’s try a couple of practice problems!
Arc Length Practice Question 1
Find the arc length over [0, π] for the parametric curve and .
Here’s how we can go about this question. First, we can begin by finding taking the derivatives of and .
Recall that the formula for arc length is .
We are given the values of and in the problem. We know that and . All we have left to do is substitute our values into the problem and solve it.
We can simplify to which is equivalent to 1!
And we have our answer! The arc length is .
Arc Length Practice Question 2
Let’s try solving another problem!
Find the arc length over [0, π] for the parametric curve and .
Once again, we can begin by finding taking the derivatives of and .
The formula for arc length is .
Like last time, we are given the values of and in the problem. We know that and .
Now we have to substitute our values into the problem and solve it.
And we have our answer! The arc length is .
⭐ Closing
These problems rarely get tougher than this!! The difficult part is integrating the equations. Once you get the hang of integrating, you will be easily able to solve these problems :)
<< Hide Menu
9.3 Finding Arc Lengths of Curves Given by Parametric Equations
5 min read•june 18, 2024
9.3 Finding Arc Lengths of Curves Given by Parametric Equations
For this portion of the AP Calculus BC course, we will learn how to apply what we have previously learned about arc length to parametric curves. To learn more about finding arc lengths of smooth planar curves, please refer to the Unit 8.13 study guide!
🏹 Reviewing Arc Length
In calculus, the arc length of a curve refers to the distance between two points on a curve. For example, if we were to mark two points on a paperclip, we could measure the arc length between those two points by unraveling the paperclip. Once the paperclip is straightened out, we can use a ruler to measure the distance between those two points. A similar strategy is used to measure the arc length of a curve.

Image Courtesy of Math Is Fun
✏️ Derivation of Arc Length Formula (Cartesian)
This image above depicts how calculus can be used to calculate the arc length of curves. The process essentially involves using the Pythagorean Theorem, , to find the hypotenuse of a triangle with side lengths of and . By adding up all the little hypotenuses, we can get a good approximation for the arc length of the curve. The arc length formula is derived from this idea. The derivation is shown in greater detail below:
However, this formula is only used to find the arc length of smooth planar curves. We need to adapt the formula a little more in order to use it for parametric curves!
💭 Arc Length of Parametric Curves
Review of Parametric Equations
To understand how the arc length formula needs to be adapted for parametric equations, it’s important that you first understand the relationship between parametric and Cartesian equations. The diagram below does a great job of helping us visualize this relationship!

Image Courtesy of GeoGebra
As can be seen in the image, while .
✏️ Deriving the Arc Length Formula (Parametric)
Earlier, we derived the arc length formula for cartesian curves. When we substitute for for their parametric equivalents, and , we arrive at the arc length formula for parametric curves. This process is shown below:
Notice that the formula looks similar to the case of the Cartesian equation. However, both x and y are changing, so we need to account for both of their fluctuations!
📝 Arc Length—Parametric Practice
Now that we know the formula for finding the arc length of parametric curves, let’s try a couple of practice problems!
Arc Length Practice Question 1
Find the arc length over [0, π] for the parametric curve and .
Here’s how we can go about this question. First, we can begin by finding taking the derivatives of and .
Recall that the formula for arc length is .
We are given the values of and in the problem. We know that and . All we have left to do is substitute our values into the problem and solve it.
We can simplify to which is equivalent to 1!
And we have our answer! The arc length is .
Arc Length Practice Question 2
Let’s try solving another problem!
Find the arc length over [0, π] for the parametric curve and .
Once again, we can begin by finding taking the derivatives of and .
The formula for arc length is .
Like last time, we are given the values of and in the problem. We know that and .
Now we have to substitute our values into the problem and solve it.
And we have our answer! The arc length is .
⭐ Closing
These problems rarely get tougher than this!! The difficult part is integrating the equations. Once you get the hang of integrating, you will be easily able to solve these problems :)

© 2025 Fiveable Inc. All rights reserved.