Browse By Unit
9.2 Second Derivatives of Parametric Equations
3 min read•june 18, 2024
Sumi Vora
Jed Quiaoit
Sumi Vora
Jed Quiaoit
9.2 Second Derivatives of Parametric Equations
Refresher time! Recall from 9.1 Defining and Differentiating Parametric Equations the following ideas:
- Parametric functions are functions in which independent functions x and y are connected via t, a dummy variable representing time.
- To calculate derivatives of parametric equations, , we first find (from y(t)) and (from x(t)) and then divide the former by the latter.
- Parametric equations are useful in determining the slope of a tangent line at a given point; more broadly speaking, they can inform us about rates of change of physical phenomena like motion.
As point (2) emphasized, we left 9.1 with the toolkit to calculate the first derivative of curves derived parametrically. This section, on the other hand, focuses on computing the second derivative of parametric equations we’ve been describing so far. 🧠
🤔 Finding Second Derivatives of Parametric Equations
Put simply, we denote the second derivative of a parametric function as follows:
To find said derivative, we’ll use the chain rule: ⛓️
🔨 Breaking Down the Second Derivative
Here's a more in-depth description of the formula above:
Like in any other function, finding the second derivative of a parametric function involves taking the derivative of the first derivative of the function. In order to do this, we first need to find the first derivative of the parametric function, which is known as the parametric derivative as seen in 9.1. 🛒
Once we have found the parametric derivative, we can then take the derivative of this equation with respect to the parameter to find the second derivative. This is done by taking the derivative of both sides of the equation with respect to the parameter.
On the left side of the derivation above, the second derivative is denoted as . On the right side, the second derivative is found by taking the derivative of the ratio with respect to the parameter.
This can be done using the quotient rule for derivatives, which states that the derivative of a ratio is equal to the difference of the product of the derivative of the numerator and the denominator, and the product of the numerator and the derivative of the denominator, all divided by the square of the denominator. ➗
You might wonder: “The derivation looks so complex!” 😵💫 Good news: you don’t need to remember the entire step-by-step process. If you do have the time and energy, it’d be nice learning-wise to be able to derive the second derivative. Otherwise, focus on the last term:
Like finding first derivatives, calculating second derivatives for parametric equation become more natural with practice. That being said, let’s work out a couple examples! 🤓
✏️ Practice Finding Second Derivative of Parametric Functions
We have three questions here for you, with detailed explanations!
🥇 Second Derivative: Example 1
Show that the cycloid defined by and is concave down on .
Finding dx/dt and dy/dt:
Putting these two together to find dy/dx, the first derivative:
To find the second derivative, we derive dy/dx again and divide this derivative by dx/dt. The numerator will, thus, look like this after deriving using the quotient rule:
Divide this by dx/dt to get our second derivative… we can further simplify, too!
Applying the trig identity sin²(t)-cos²(t) = 1:
Since the second derivative is always negative in this equation, the cycloid will always be concave down!
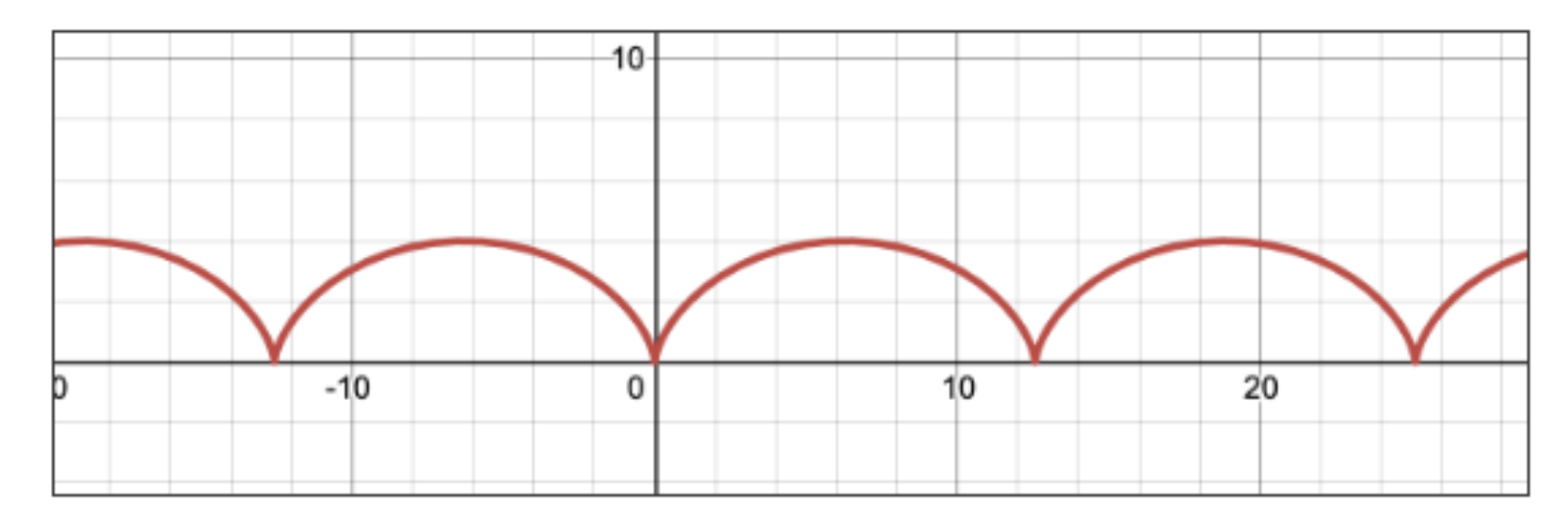
Courtesy of Desmos
🥈 Second Derivative: Example 2
Consider the parametric equations and . Find the second derivative of y with respect to x.
Finding dx/dt and dy/dt:
Putting these two together to find dy/dx, the first derivative:
Deriving dy/dx:
Divide this by dx/dt to get our second derivative… we can further simplify, too!
🥉 Second Derivative: Example 3
A car is moving along a curved road that can be represented by the parametric equations and . What is the value of the second derivative of y with respect to x?
Finding dx/dt and dy/dt:
Putting these two together to find dy/dx, the first derivative:
Deriving dy/dx:
Divide this by dx/dt to get our second derivative… we can further simplify, too!
You made it through!
⭐ Closing
Feeling better? Although slightly more convoluted than first derivative calculations, writing down each of the steps helps significantly in making sure you get the right answers at the end. Woo-hoo! 🎈
<< Hide Menu
9.2 Second Derivatives of Parametric Equations
3 min read•june 18, 2024
Sumi Vora
Jed Quiaoit
Sumi Vora
Jed Quiaoit
9.2 Second Derivatives of Parametric Equations
Refresher time! Recall from 9.1 Defining and Differentiating Parametric Equations the following ideas:
- Parametric functions are functions in which independent functions x and y are connected via t, a dummy variable representing time.
- To calculate derivatives of parametric equations, , we first find (from y(t)) and (from x(t)) and then divide the former by the latter.
- Parametric equations are useful in determining the slope of a tangent line at a given point; more broadly speaking, they can inform us about rates of change of physical phenomena like motion.
As point (2) emphasized, we left 9.1 with the toolkit to calculate the first derivative of curves derived parametrically. This section, on the other hand, focuses on computing the second derivative of parametric equations we’ve been describing so far. 🧠
🤔 Finding Second Derivatives of Parametric Equations
Put simply, we denote the second derivative of a parametric function as follows:
To find said derivative, we’ll use the chain rule: ⛓️
🔨 Breaking Down the Second Derivative
Here's a more in-depth description of the formula above:
Like in any other function, finding the second derivative of a parametric function involves taking the derivative of the first derivative of the function. In order to do this, we first need to find the first derivative of the parametric function, which is known as the parametric derivative as seen in 9.1. 🛒
Once we have found the parametric derivative, we can then take the derivative of this equation with respect to the parameter to find the second derivative. This is done by taking the derivative of both sides of the equation with respect to the parameter.
On the left side of the derivation above, the second derivative is denoted as . On the right side, the second derivative is found by taking the derivative of the ratio with respect to the parameter.
This can be done using the quotient rule for derivatives, which states that the derivative of a ratio is equal to the difference of the product of the derivative of the numerator and the denominator, and the product of the numerator and the derivative of the denominator, all divided by the square of the denominator. ➗
You might wonder: “The derivation looks so complex!” 😵💫 Good news: you don’t need to remember the entire step-by-step process. If you do have the time and energy, it’d be nice learning-wise to be able to derive the second derivative. Otherwise, focus on the last term:
Like finding first derivatives, calculating second derivatives for parametric equation become more natural with practice. That being said, let’s work out a couple examples! 🤓
✏️ Practice Finding Second Derivative of Parametric Functions
We have three questions here for you, with detailed explanations!
🥇 Second Derivative: Example 1
Show that the cycloid defined by and is concave down on .
Finding dx/dt and dy/dt:
Putting these two together to find dy/dx, the first derivative:
To find the second derivative, we derive dy/dx again and divide this derivative by dx/dt. The numerator will, thus, look like this after deriving using the quotient rule:
Divide this by dx/dt to get our second derivative… we can further simplify, too!
Applying the trig identity sin²(t)-cos²(t) = 1:
Since the second derivative is always negative in this equation, the cycloid will always be concave down!

Courtesy of Desmos
🥈 Second Derivative: Example 2
Consider the parametric equations and . Find the second derivative of y with respect to x.
Finding dx/dt and dy/dt:
Putting these two together to find dy/dx, the first derivative:
Deriving dy/dx:
Divide this by dx/dt to get our second derivative… we can further simplify, too!
🥉 Second Derivative: Example 3
A car is moving along a curved road that can be represented by the parametric equations and . What is the value of the second derivative of y with respect to x?
Finding dx/dt and dy/dt:
Putting these two together to find dy/dx, the first derivative:
Deriving dy/dx:
Divide this by dx/dt to get our second derivative… we can further simplify, too!
You made it through!
⭐ Closing
Feeling better? Although slightly more convoluted than first derivative calculations, writing down each of the steps helps significantly in making sure you get the right answers at the end. Woo-hoo! 🎈

© 2025 Fiveable Inc. All rights reserved.