Browse By Unit
Dalia Savy
Kanya Shah
Dalia Savy
Kanya Shah
Ideal gases are exactly that: ideal! This term is used to describe the behavior of theoretical gases that follow the ideal gas law exactly, which is what we went over in the last key topic. Our focus here is the Kinetic Molecular Theory, which describes the behavior of ideal gases.♨️
Fun Fact: two gases that behave the most ideally in the real world are H2 and He because they are really small and non-polar particles. PLIGHT [pressure low, ideal gas, high temp] are the conditions of temperature and pressure when gases behave most ideally. We'll learn more about that in the next key unit!
The Kinetic Molecular Theory (KMT)
Kinetic Energy (KE)
If you recall from the last key topic, temperature is directly related to the average kinetic energy of particles in a substance. Therefore, as temperature increases, the gaseous particles move faster. The average kinetic energy of a gas particle can be calculated by using the following equation:
KE = 1/2mv^2, where
- m = mass of the molecule (kg)
- v = speed🏃 of the molecule (m/s)
- KE is measured in joules
- This formula doesn't have to be memorized since it is on the given reference sheet, but it is essential to understanding kinetic energy. All particles in every sample of matter have some sort of motion; particles are continuously moving randomly! The speed at which they are doing so all depends on temperature and other conditions.
The Theory
There are five main assumptions of the Kinetic Molecular Theory:
- There are no attractive or repulsive forces between gas particles.
- The particles of an ideal gas are separated by great distances compared to their size (gas particles have negligible, or no, volume because of how small and spread apart particles are).
- Gas particles move in random, constant, straight-line motion.
- Collisions are elastic: when gas particles collide, they transfer energy without a net loss - no energy is lost.
- When observing particles, their kinetic energy is directly related to their velocity (KE = 1/2mv^2). All gases have the same average kinetic energy at a given temperature.
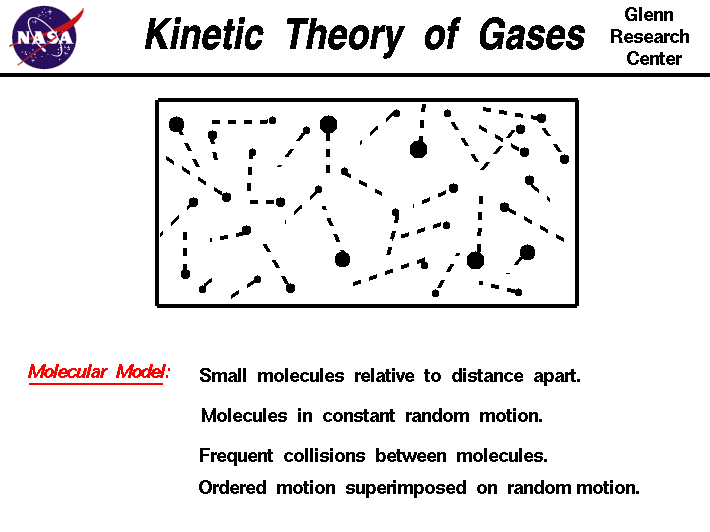
Photo Courtesy of NASA
Maxwell-Boltzmann Distributions
Maxwell-Boltzmann distributions, sometimes called Boltzmann distributions, display the distribution of energy (and subsequently velocity) at given temperatures🌡️ for a gas.
Boltzmann diagrams can be really tricky to read because they can be extremely misleading at times. When you see a really high peak on a Boltzmann distribution, that does NOT mean that at that temperature particles have more energy, rather it means that a higher NUMBER of particles have that energy. Taking a look at an image of a few distributions may help:
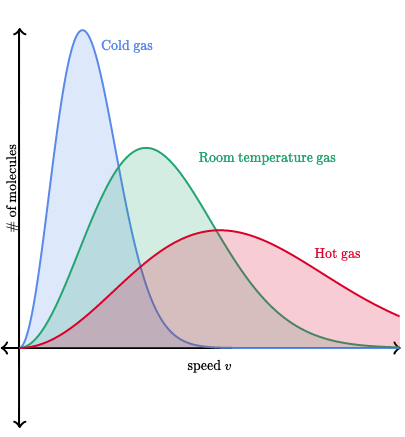
Image Courtesy of DeepAI
Here we have three distributions: one gas that is cold, one gas that is at room temperature, and another that is hot. At first glance, the cold gas might seem to have the highest speed, but take a look at the axes.
On the x-axis, we have the speed (and energy, since KE = 1/2mv^2) and on the y-axis, we see the number of molecules. This means that the high peak for the cold gas means that a large number of gas particles actually have a slower speed. Looking at the hotter gasses, we can see more molecules having a faster speed, and thus more energy.
💡Remember: The Maxwell-Boltzmann Distributions show that as temperature increases, the range of velocities become larger and particles move at a higher speed. If the diagram were to have curves that represent different types of gases instead of temperatures, as the element gets lighter, the range of velocities becomes larger. You should correlate particles at higher temperatures🌡️ with having the same curve as a light gas.
That's all you really have to know for AP Chem! This is more of an AP Physics topic, so just remember that one fact and the diagram, and you're good to go.
AP Free-Response: 2019 #4
The following question is from the 2019 AP Examination, number 4 on the FRQ section.
A student is doing experiments with CO2(g). Originally, a sample of gas is in a rigid container at 299K and 0.70 atm. The student increases the temperature of the CO2(g) in the container to 425K.
- Describe the effect of raising the temperature on the motion of the CO2(g) molecules.
- Calculate the pressure of the CO2(g) in the container at 425K.
- In terms of the kinetic molecular theory, briefly explain why the pressure of the CO2(g) in the container changes as it is heated to 425K.
Sample Responses
Working through a gas law FRQ, it is good to note what information you are given:
- Rigid container --> the gas cannot escape so fixed volume
- Initial Temperature --> 299 K
- Initial Pressure --> 0.70 atm
- Experiment --> temperature being increased to 425K so 425K is the final temperature.
#1 Breakdown
The first part is asking you to describe something, so we have to write 1-2 sentences describing the phenomenon using the knowledge we know.
As you can recall, raising the temperature increases the speed of the molecules and we should always use the phrase "average kinetic energy" in our answer.
Sample Response: As you increase the temperature, or the average kinetic energy, of the CO2(g) molecules, the speed of the molecules increases as well.
#2 Breakdown
The second part is asking you to calculate something, so we will have to use any equation we learned about so far to find a missing piece of information.
The question is asking you to calculate the final pressure after the experiment has occurred. This question is really simple once you look at the information we were given and noted down at the beginning!
We could easily use the combined gas law, or P1V1/T1 = P2V2/T2 for this equation.
Since we know that the volume is fixed, or constant, we can eliminate it from the equation and use P1/T1 = P2/T2, which is really Gay-Lussac's gas law.
Once we plug in what we have, we get 0.70 atm/299 K = P2/425 K, which gets us 0.99 atm.
On your AP Exam, it would be good to show the original formula, the substitution, and the final answer with units (which is what I bolded) for full credit and an amazing response.
#3 Breakdown
The third part is asking you to explain, so there should be a few sentences.
Sample Response: Faster-moving gas particles collide more frequently and forcefully with the walls of the container, increasing the overall pressure.
<< Hide Menu
Dalia Savy
Kanya Shah
Dalia Savy
Kanya Shah
Ideal gases are exactly that: ideal! This term is used to describe the behavior of theoretical gases that follow the ideal gas law exactly, which is what we went over in the last key topic. Our focus here is the Kinetic Molecular Theory, which describes the behavior of ideal gases.♨️
Fun Fact: two gases that behave the most ideally in the real world are H2 and He because they are really small and non-polar particles. PLIGHT [pressure low, ideal gas, high temp] are the conditions of temperature and pressure when gases behave most ideally. We'll learn more about that in the next key unit!
The Kinetic Molecular Theory (KMT)
Kinetic Energy (KE)
If you recall from the last key topic, temperature is directly related to the average kinetic energy of particles in a substance. Therefore, as temperature increases, the gaseous particles move faster. The average kinetic energy of a gas particle can be calculated by using the following equation:
KE = 1/2mv^2, where
- m = mass of the molecule (kg)
- v = speed🏃 of the molecule (m/s)
- KE is measured in joules
- This formula doesn't have to be memorized since it is on the given reference sheet, but it is essential to understanding kinetic energy. All particles in every sample of matter have some sort of motion; particles are continuously moving randomly! The speed at which they are doing so all depends on temperature and other conditions.
The Theory
There are five main assumptions of the Kinetic Molecular Theory:
- There are no attractive or repulsive forces between gas particles.
- The particles of an ideal gas are separated by great distances compared to their size (gas particles have negligible, or no, volume because of how small and spread apart particles are).
- Gas particles move in random, constant, straight-line motion.
- Collisions are elastic: when gas particles collide, they transfer energy without a net loss - no energy is lost.
- When observing particles, their kinetic energy is directly related to their velocity (KE = 1/2mv^2). All gases have the same average kinetic energy at a given temperature.

Photo Courtesy of NASA
Maxwell-Boltzmann Distributions
Maxwell-Boltzmann distributions, sometimes called Boltzmann distributions, display the distribution of energy (and subsequently velocity) at given temperatures🌡️ for a gas.
Boltzmann diagrams can be really tricky to read because they can be extremely misleading at times. When you see a really high peak on a Boltzmann distribution, that does NOT mean that at that temperature particles have more energy, rather it means that a higher NUMBER of particles have that energy. Taking a look at an image of a few distributions may help:

Image Courtesy of DeepAI
Here we have three distributions: one gas that is cold, one gas that is at room temperature, and another that is hot. At first glance, the cold gas might seem to have the highest speed, but take a look at the axes.
On the x-axis, we have the speed (and energy, since KE = 1/2mv^2) and on the y-axis, we see the number of molecules. This means that the high peak for the cold gas means that a large number of gas particles actually have a slower speed. Looking at the hotter gasses, we can see more molecules having a faster speed, and thus more energy.
💡Remember: The Maxwell-Boltzmann Distributions show that as temperature increases, the range of velocities become larger and particles move at a higher speed. If the diagram were to have curves that represent different types of gases instead of temperatures, as the element gets lighter, the range of velocities becomes larger. You should correlate particles at higher temperatures🌡️ with having the same curve as a light gas.
That's all you really have to know for AP Chem! This is more of an AP Physics topic, so just remember that one fact and the diagram, and you're good to go.
AP Free-Response: 2019 #4
The following question is from the 2019 AP Examination, number 4 on the FRQ section.
A student is doing experiments with CO2(g). Originally, a sample of gas is in a rigid container at 299K and 0.70 atm. The student increases the temperature of the CO2(g) in the container to 425K.
- Describe the effect of raising the temperature on the motion of the CO2(g) molecules.
- Calculate the pressure of the CO2(g) in the container at 425K.
- In terms of the kinetic molecular theory, briefly explain why the pressure of the CO2(g) in the container changes as it is heated to 425K.
Sample Responses
Working through a gas law FRQ, it is good to note what information you are given:
- Rigid container --> the gas cannot escape so fixed volume
- Initial Temperature --> 299 K
- Initial Pressure --> 0.70 atm
- Experiment --> temperature being increased to 425K so 425K is the final temperature.
#1 Breakdown
The first part is asking you to describe something, so we have to write 1-2 sentences describing the phenomenon using the knowledge we know.
As you can recall, raising the temperature increases the speed of the molecules and we should always use the phrase "average kinetic energy" in our answer.
Sample Response: As you increase the temperature, or the average kinetic energy, of the CO2(g) molecules, the speed of the molecules increases as well.
#2 Breakdown
The second part is asking you to calculate something, so we will have to use any equation we learned about so far to find a missing piece of information.
The question is asking you to calculate the final pressure after the experiment has occurred. This question is really simple once you look at the information we were given and noted down at the beginning!
We could easily use the combined gas law, or P1V1/T1 = P2V2/T2 for this equation.
Since we know that the volume is fixed, or constant, we can eliminate it from the equation and use P1/T1 = P2/T2, which is really Gay-Lussac's gas law.
Once we plug in what we have, we get 0.70 atm/299 K = P2/425 K, which gets us 0.99 atm.
On your AP Exam, it would be good to show the original formula, the substitution, and the final answer with units (which is what I bolded) for full credit and an amazing response.
#3 Breakdown
The third part is asking you to explain, so there should be a few sentences.
Sample Response: Faster-moving gas particles collide more frequently and forcefully with the walls of the container, increasing the overall pressure.

© 2025 Fiveable Inc. All rights reserved.