Browse By Unit
Dalia Savy
Kanya Shah
Dalia Savy
Kanya Shah
Quantum Mechanics: Where is the Electron?
In the early days of chemistry, there were models of the atom all over the place. ⚛️
The first true model of an "atom" was the Dalton Model, which represented atoms as small indivisible and indestructible balls bouncing off of each other. Of course, as you've learned in unit one, atoms aren't quite so simple.
The next model that came was Thomson's Plum Pudding Model🍮 in the late 19th century, shortly after J.J. Thompson discovered the electron. This model represented the atom as a sea of positive charge with specks of negative charge - the electrons, like raisins in a plum pudding.
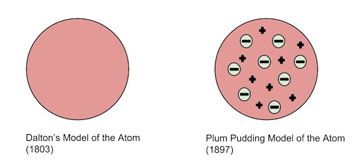
Image Courtesy of Study
From this point on, scientists knew two things about the model of the atom: there's a positive part and a negative part. They kept observing that the current model of the atom did not properly explain the observed properties, so more experiments were done and the model kept altering.
From here, Rutherford conducted the gold foil experiment in the early 20th century 💛. He fired a beam of positive alpha particles at a thin sheet of gold foil and measured their deflections. His results were that most of the alpha particles passed straight through the foil, but some deflected at large angles.
Rutherford concluded that the positive charge in an atom is concentrated in a small, dense nucleus at the center of the atom, surrounded by a lot of empty space and a cloud of electrons. The biggest shock at the time was how his gold foil experiment showed that most of the atom was empty space.
👉While you don't need to necessarily know all of this history and all of these models for the AP Exam, understanding the foundations of chemistry help to build a foundation for the fundamental question for all of these models, and the question that created the field of quantum mechanics: where the heck do the electrons go?
While we won't exactly answer that exact question in this unit, it will be answered in part when you learn about electron orbitals.
Max Planck and the Ultraviolet Catastrophe
To understand where the electrons are in an atom, we must first understand how light and energy work together to form the basis for the quantum world. As we learned in the last lesson, light can be represented as a wave of electromagnetic radiation permeating space.💡
One of the most important observations made was that when a piece of metal, or any substance for that matter, was heated up enough, it released light. This makes sense! If you think about someone like a blacksmith, they take glowing hot metal and pound it into shape.
When discussing why exactly this happens, scientists hypothesized about a body that absorbed all light, known as a blackbody. It only absorbed and emitted light; it did not reflect any. However, when discussing light being radiated from a blackbody, it became clear that with this model, a body emits infinite amounts of light and thus infinite amounts of energy, creating the ultraviolet catastrophe. This theory broke laws of conservation of energy and frankly logic. When you put toast🍞 in a toaster, it does not burn your toast to smithereens, despite, according to the classical model, a blackbody should emit infinite energy.
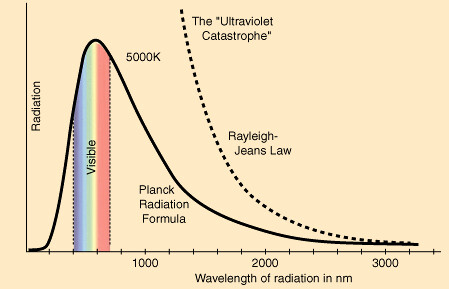
The Ultraviolet Catastrophe. Image Courtesy of MSE 5317
Max Planck to the Rescue!
However, shortly after this catastrophe, a physicist named Max Planck solved the puzzle🧩. He theorized that light is emitted in discrete quantities - quanta (hence, quantum mechanics), in which energy is proportional to the frequency of the wave.
This can be represented in the equation E = hν, where E is the energy, ν is the frequency and h is Planck's constant.
h = Planck's constant = 6.626 * 10^-34 Js (Joule seconds) - on the AP reference table
This equation helped form the basis for the eventual creation of quantum mechanics.
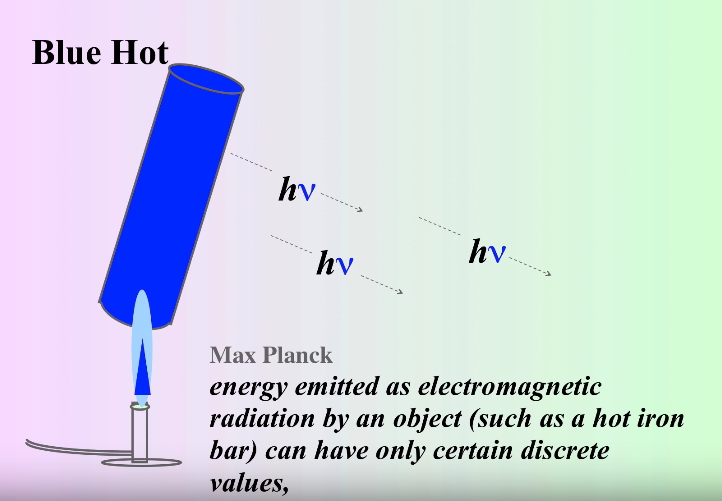
Quantized Light, Image Courtesy of MisterChemistry
The Photoelectric Effect
However, Planck's discovery was not immediately seen as revolutionary. It was not clear how amazing this discovery was until Albert Einstein uncovered the Photoelectric Effect, yet another mystery in physics.
Experiments showed that electrons were ejected from the surface of certain metals exposed to light of a minimum threshold frequency (and thus, as we've discussed, a minimum energy). Essentially, if you take a high enough frequency of light, you can zap electrons off of the surface of a metal, and this boggled the minds of physicists🤯. Einstein theorized that this was Planck's theory at work. ⚡
He theorized that light, in this case, was working like a particle - photons. Mathematically, this can be represented as saying hv = KE of the electron + binding energy of the electron.
Because we know the hν is the energy of a wave of light (or now a photon), we know that if the energy of a photon exceeds the binding energy of an electron, the electron will be zapped away. Then, once we reach the threshold frequency, the kinetic energy of the photon increases as we lower the wavelength (or up the frequency, same thing) of the light.
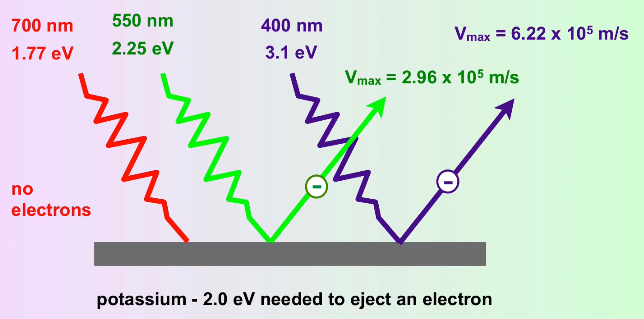
Image Courtesy of MisterChemistry
To put it in simpler words, the photoelectric effect only occurs if the frequency of light reaches a certain threshold:
- If the frequency is low, the metal absorbs the light. It is not high enough to reach the threshold and therefore does not exhibit the photoelectric effect.
- If the frequency is high enough and reaches the threshold, a specified number of electrons are ejected from the metal. 🎥Watch AP Chemistry teacher Mónica Gracida teach the photoelectric effect and review the concepts of wavelength, frequency, and energy of a wave.
Speed of Light
There is one more equation to keep in mind besides E=hν and it relates the speed of light to both wavelength and frequency. As we discussed in the last key topic, frequency and wavelength are inversely related: c = λν.
c = speed of light = 2.998 x 10^8 m/s
This equation is usually used in combination with the previous one. Together, they can help you solve a free-response question (FRQ) on the exam. Luckily, they are both listed on the AP Chemistry reference table🥳. If you'd like to solve a previous AP FRQ, check out the next study guide and key topic.
<< Hide Menu
Dalia Savy
Kanya Shah
Dalia Savy
Kanya Shah
Quantum Mechanics: Where is the Electron?
In the early days of chemistry, there were models of the atom all over the place. ⚛️
The first true model of an "atom" was the Dalton Model, which represented atoms as small indivisible and indestructible balls bouncing off of each other. Of course, as you've learned in unit one, atoms aren't quite so simple.
The next model that came was Thomson's Plum Pudding Model🍮 in the late 19th century, shortly after J.J. Thompson discovered the electron. This model represented the atom as a sea of positive charge with specks of negative charge - the electrons, like raisins in a plum pudding.

Image Courtesy of Study
From this point on, scientists knew two things about the model of the atom: there's a positive part and a negative part. They kept observing that the current model of the atom did not properly explain the observed properties, so more experiments were done and the model kept altering.
From here, Rutherford conducted the gold foil experiment in the early 20th century 💛. He fired a beam of positive alpha particles at a thin sheet of gold foil and measured their deflections. His results were that most of the alpha particles passed straight through the foil, but some deflected at large angles.
Rutherford concluded that the positive charge in an atom is concentrated in a small, dense nucleus at the center of the atom, surrounded by a lot of empty space and a cloud of electrons. The biggest shock at the time was how his gold foil experiment showed that most of the atom was empty space.
👉While you don't need to necessarily know all of this history and all of these models for the AP Exam, understanding the foundations of chemistry help to build a foundation for the fundamental question for all of these models, and the question that created the field of quantum mechanics: where the heck do the electrons go?
While we won't exactly answer that exact question in this unit, it will be answered in part when you learn about electron orbitals.
Max Planck and the Ultraviolet Catastrophe
To understand where the electrons are in an atom, we must first understand how light and energy work together to form the basis for the quantum world. As we learned in the last lesson, light can be represented as a wave of electromagnetic radiation permeating space.💡
One of the most important observations made was that when a piece of metal, or any substance for that matter, was heated up enough, it released light. This makes sense! If you think about someone like a blacksmith, they take glowing hot metal and pound it into shape.
When discussing why exactly this happens, scientists hypothesized about a body that absorbed all light, known as a blackbody. It only absorbed and emitted light; it did not reflect any. However, when discussing light being radiated from a blackbody, it became clear that with this model, a body emits infinite amounts of light and thus infinite amounts of energy, creating the ultraviolet catastrophe. This theory broke laws of conservation of energy and frankly logic. When you put toast🍞 in a toaster, it does not burn your toast to smithereens, despite, according to the classical model, a blackbody should emit infinite energy.

The Ultraviolet Catastrophe. Image Courtesy of MSE 5317
Max Planck to the Rescue!
However, shortly after this catastrophe, a physicist named Max Planck solved the puzzle🧩. He theorized that light is emitted in discrete quantities - quanta (hence, quantum mechanics), in which energy is proportional to the frequency of the wave.
This can be represented in the equation E = hν, where E is the energy, ν is the frequency and h is Planck's constant.
h = Planck's constant = 6.626 * 10^-34 Js (Joule seconds) - on the AP reference table
This equation helped form the basis for the eventual creation of quantum mechanics.

Quantized Light, Image Courtesy of MisterChemistry
The Photoelectric Effect
However, Planck's discovery was not immediately seen as revolutionary. It was not clear how amazing this discovery was until Albert Einstein uncovered the Photoelectric Effect, yet another mystery in physics.
Experiments showed that electrons were ejected from the surface of certain metals exposed to light of a minimum threshold frequency (and thus, as we've discussed, a minimum energy). Essentially, if you take a high enough frequency of light, you can zap electrons off of the surface of a metal, and this boggled the minds of physicists🤯. Einstein theorized that this was Planck's theory at work. ⚡
He theorized that light, in this case, was working like a particle - photons. Mathematically, this can be represented as saying hv = KE of the electron + binding energy of the electron.
Because we know the hν is the energy of a wave of light (or now a photon), we know that if the energy of a photon exceeds the binding energy of an electron, the electron will be zapped away. Then, once we reach the threshold frequency, the kinetic energy of the photon increases as we lower the wavelength (or up the frequency, same thing) of the light.

Image Courtesy of MisterChemistry
To put it in simpler words, the photoelectric effect only occurs if the frequency of light reaches a certain threshold:
- If the frequency is low, the metal absorbs the light. It is not high enough to reach the threshold and therefore does not exhibit the photoelectric effect.
- If the frequency is high enough and reaches the threshold, a specified number of electrons are ejected from the metal. 🎥Watch AP Chemistry teacher Mónica Gracida teach the photoelectric effect and review the concepts of wavelength, frequency, and energy of a wave.
Speed of Light
There is one more equation to keep in mind besides E=hν and it relates the speed of light to both wavelength and frequency. As we discussed in the last key topic, frequency and wavelength are inversely related: c = λν.
c = speed of light = 2.998 x 10^8 m/s
This equation is usually used in combination with the previous one. Together, they can help you solve a free-response question (FRQ) on the exam. Luckily, they are both listed on the AP Chemistry reference table🥳. If you'd like to solve a previous AP FRQ, check out the next study guide and key topic.

© 2025 Fiveable Inc. All rights reserved.