Browse By Unit
Dalia Savy
Dalia Savy
This unit is all about learning and identifying different chemical reactions. One of the learning objectives of unit four in the AP Chemistry course is to "identify a reaction as acid-base, oxidation-reduction, or precipitation."
Types of Reactions
Throughout this unit's study guides, you've gotten a taste of net ionic equations and precipitation reactions, as well as titrations and acid-base reactions. Oxidation-reduction reactions are going to be reviewed in-depth in the rest of this unit. For now, here is a quick rundown of these three types of reactions:
- Acid-base reactions are chemical reactions that involve the transfer of a proton from one molecule to another. They often involve the transfer of a proton from a strong acid to a strong base, resulting in the formation of a salt and water. For more about acid-base reactions, check out the next study guide.
- Oxidation-reduction reactions, also known as redox reactions, are chemical reactions in which the atoms of one or more elements are oxidized (lose electrons) and reduced (gain electrons). These reactions involve the transfer of electrons from a reducing agent to an oxidizing agent and are characterized by a change in the oxidation state of the elements involved in the reaction. 1. Combustion reactions are a type of redox reaction and you've already learned about them! The specifics and must-know information about redox reactions will be covered later in this unit.
- Precipitation reactions are chemical reactions in which two or more soluble reactants combine to form an insoluble product, which is known as a precipitate. We'll focus on precipitation reactions in this study guide!
Precipitation Reactions Explained
When ions in aqueous solutions react, they may produce an insoluble (undissolvable) or barely soluble solid ionic compound. This solid product is called a precipitate.
Solubility Rules
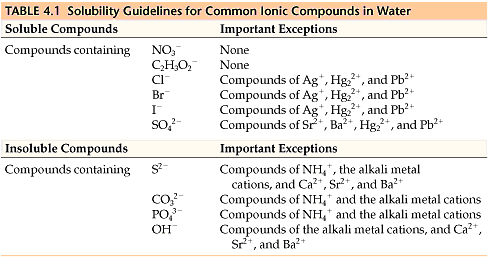
All sodium, potassium, and nitrate salts🧂 are soluble in water, so they aren’t precipitates. You don’t need to know any other solubility rules for the AP, but it doesn’t hurt to be familiar with common soluble and insoluble compounds. Table 4.1 is a table of solubility for common ions in water. Usually, the question will tell you if the compound is soluble and which solution it’s soluble in. 😊
Net Ionic Equations
We went over this in key topic 4.2, but let's do a quick overview! 🏃
The best steps to follow when writing a net ionic equation are:
- Figure out which compounds are soluble and insoluble using solubility rules.
- Balance the chemical equation. It may already be balanced, but it also may not, so you always have to check.
- Write the complete ionic equation by dissociating soluble compounds into ions.
- Omit the spectator ions and write the final net ionic equation of the given reaction. Make sure you include the phase of matter each compound is in.
Concentration of Ions
Knowing how to write the net ionic equation for a precipitation reaction is just the first step! Let's take a look at a concentration of ions question, where you calculate how much of each ion is present after a precipitation reaction.
Question: 20.0 mL of [0.100] NaCl (aq) reacts with 30.0 mL of [0.0400] Pb(C₂H₃O₂)₂ (aq).
Part a: What is the mass of the solid formed?
Part b: What are the concentrations of ions at the end of the reaction?
Step #1
Since they didn't give us the equation, let's write it ourselves!
NaCl + Pb(C₂H₃O₂)₂ → NaC₂H₃O₂ + PbCl₂
Always check the equation is balanced! This one isn't, so let's balance it out and make sure each ion is in equal amounts on both sides. 2NaCl + Pb(C₂H₃O₂)₂ → 2NaC₂H₃O₂ + PbCl₂
Step #2
With precipitation reactions and concentration of ions questions, there will always be an insoluble product. In this case, it is either NaC₂H₃O₂ or PbCl₂. Since sodium is always soluble, PbCl₂ is the precipitate in this question.
2NaCl (aq) + Pb(C₂H₃O₂)₂ (aq) → 2NaC₂H₃O₂ (aq) + PbCl₂ (s)
Step #3
Now that we have the equation and know the precipitate, let's get into the math itself. The question provided us with the volumes and molarities for each reactant. Using these two pieces of information, we can find the number of moles of NaCl and Pb(C₂H₃O₂)₂.
Molarity = moles / volume in L - We have to convert the volumes we have into L by dividing by 1000.
0.100 = x moles of NaCl / 0.020 L → x = 0.00200 moles of NaCl (aq)
0.0400 = x moles of Pb(C₂H₃O₂)₂ / 0.030 L → x = 0.00120 moles of Pb(C₂H₃O₂)₂ (aq)
Step #4
Using the number of moles we solved for above, we can now use stoichiometry to answer part a.
But wait! Which number do we do stoich with: 0.00200 or 0.00120🤔?
This is where the limiting reactant (LR) comes into play. The limiting reactant in a reaction is the substance that limits the amount of products produced. Basically, there are different amounts of each reactant. One reactant is more abundant, right?
The reactant that there is less of eventually stops the reaction and limits it since the reactant runs out. The other reactant is called the excess since there is still some of it left over, unreacted.
To find the LR, we have to do stoichiometry with both amounts. Convert each reactant into the precipitate:
Since there are less moles of PbCl₂ using NaCl as a reactant, NaCl is the LR. Pb(C₂H₃O₂)₂ is the excess.
Now we know how many moles of NaCl, Pb(C₂H₃O₂)₂, and PbCl₂ we have, wecan answer part a for real now!🥳
0.00100 mol PbCl₂ x 278.2 g/mol = 0.278 g of PbCl₂
Step #5
Yay, we did half the problem! Let's move on to solving for the concentrations of ions. In order for us to do this, we have to know the moles of each ion and the volumes of each ion.
Let's think this through conceptually a bit. After PbCl₂ (s) forms, what is left in the solution?
Looking back at the LR, either Na⁺ or Cl⁻ will have a final concentration of 0 since one of them will be completely used up. Since Cl⁻ is in the precipitate, Cl⁻ has a final concentration of 0. All of the chloride anions in the solution have been used up to form as much precipitate as possible.
That was easy! 1/4 of part b is complete. 😊
The ion that is in the LR and precipitate ALWAYS has a final concentration of 0. Think of it as being 100% used up, so there is none of it left.
Step #6
In this next step, we can solve for the concentrations of two ions: Na⁺ and C₂H₃O₂. These are considered spectator ions since they aren't in the precipitate. To find their concentrations, we have to use both the 0.00100 mol of PbCl₂ from using NaCl and the 0.00120 mol of PCl₂ from using Pb(C₂H₃O₂)₂.
The first number can help us find Na⁺ whereas the second can help us find C₂H₃O₂⁻.
Na+: All you have to do now is find the volume, but we have to multiply the number of moles by 2 since NaCl has an initial coefficient of 2. This is where balancing the reaction comes in! To find the volume, we just have to add 20.0 mL and 30.0 mL and convert to liters.
(0.00100)(2) / 0.050 L = 0.0400 M of Na⁺
C₂H₃O₂⁻: We have to multiply by 2 here as well since there was a subscript on the reactant side of the equation.
(0.00120)(2) / 0.050 L = 0.0480 M of C₂H₃O₂⁻
Step #7
We have one last ion we have to calculate the concentration of: Pb⁺². This is slightly harder to find, but with some practice, you got this! 😌
To find the excess amount of lead, convert the LR to the soluble product. Here, we would convert 0.00200 moles of NaCl to find the moles reacted. Since there is a 1:2 mole ratio, 0.00100 moles reacted. Then, we would subtract by the excess number of moles (found in step 4), which is 0.00120.
0.00120 - 0.00100 = 0.00020 moles of Pb⁺² unreacted. Then we just divide by the volume in liters, so 0.00020 moles / 0.050 L = 0.0040 M of Pb⁺².
Final Answers
Part a: 0.278 g of PbCl₂
Part b: [Cl⁻] = 0
[Na⁺] = 0.0400
[C₂H₃O₂⁻] = 0.0480
[Pb⁺²] = 0.0040
This is a very difficult question but once you practice and understand it conceptually, you'll begin to be able to get through it faster. It is honestly a lot in one question and probably won't be tested like this. However, knowing it will strengthen your overall stoichiometry skills, so it doesn't hurt! 🙃
<< Hide Menu
Dalia Savy
Dalia Savy
This unit is all about learning and identifying different chemical reactions. One of the learning objectives of unit four in the AP Chemistry course is to "identify a reaction as acid-base, oxidation-reduction, or precipitation."
Types of Reactions
Throughout this unit's study guides, you've gotten a taste of net ionic equations and precipitation reactions, as well as titrations and acid-base reactions. Oxidation-reduction reactions are going to be reviewed in-depth in the rest of this unit. For now, here is a quick rundown of these three types of reactions:
- Acid-base reactions are chemical reactions that involve the transfer of a proton from one molecule to another. They often involve the transfer of a proton from a strong acid to a strong base, resulting in the formation of a salt and water. For more about acid-base reactions, check out the next study guide.
- Oxidation-reduction reactions, also known as redox reactions, are chemical reactions in which the atoms of one or more elements are oxidized (lose electrons) and reduced (gain electrons). These reactions involve the transfer of electrons from a reducing agent to an oxidizing agent and are characterized by a change in the oxidation state of the elements involved in the reaction. 1. Combustion reactions are a type of redox reaction and you've already learned about them! The specifics and must-know information about redox reactions will be covered later in this unit.
- Precipitation reactions are chemical reactions in which two or more soluble reactants combine to form an insoluble product, which is known as a precipitate. We'll focus on precipitation reactions in this study guide!
Precipitation Reactions Explained
When ions in aqueous solutions react, they may produce an insoluble (undissolvable) or barely soluble solid ionic compound. This solid product is called a precipitate.
Solubility Rules
All sodium, potassium, and nitrate salts🧂 are soluble in water, so they aren’t precipitates. You don’t need to know any other solubility rules for the AP, but it doesn’t hurt to be familiar with common soluble and insoluble compounds. Table 4.1 is a table of solubility for common ions in water. Usually, the question will tell you if the compound is soluble and which solution it’s soluble in. 😊

Net Ionic Equations
We went over this in key topic 4.2, but let's do a quick overview! 🏃
The best steps to follow when writing a net ionic equation are:
- Figure out which compounds are soluble and insoluble using solubility rules.
- Balance the chemical equation. It may already be balanced, but it also may not, so you always have to check.
- Write the complete ionic equation by dissociating soluble compounds into ions.
- Omit the spectator ions and write the final net ionic equation of the given reaction. Make sure you include the phase of matter each compound is in.
Concentration of Ions
Knowing how to write the net ionic equation for a precipitation reaction is just the first step! Let's take a look at a concentration of ions question, where you calculate how much of each ion is present after a precipitation reaction.
Question: 20.0 mL of [0.100] NaCl (aq) reacts with 30.0 mL of [0.0400] Pb(C₂H₃O₂)₂ (aq).
Part a: What is the mass of the solid formed?
Part b: What are the concentrations of ions at the end of the reaction?
Step #1
Since they didn't give us the equation, let's write it ourselves!
NaCl + Pb(C₂H₃O₂)₂ → NaC₂H₃O₂ + PbCl₂
Always check the equation is balanced! This one isn't, so let's balance it out and make sure each ion is in equal amounts on both sides. 2NaCl + Pb(C₂H₃O₂)₂ → 2NaC₂H₃O₂ + PbCl₂
Step #2
With precipitation reactions and concentration of ions questions, there will always be an insoluble product. In this case, it is either NaC₂H₃O₂ or PbCl₂. Since sodium is always soluble, PbCl₂ is the precipitate in this question.
2NaCl (aq) + Pb(C₂H₃O₂)₂ (aq) → 2NaC₂H₃O₂ (aq) + PbCl₂ (s)
Step #3
Now that we have the equation and know the precipitate, let's get into the math itself. The question provided us with the volumes and molarities for each reactant. Using these two pieces of information, we can find the number of moles of NaCl and Pb(C₂H₃O₂)₂.
Molarity = moles / volume in L - We have to convert the volumes we have into L by dividing by 1000.
0.100 = x moles of NaCl / 0.020 L → x = 0.00200 moles of NaCl (aq)
0.0400 = x moles of Pb(C₂H₃O₂)₂ / 0.030 L → x = 0.00120 moles of Pb(C₂H₃O₂)₂ (aq)
Step #4
Using the number of moles we solved for above, we can now use stoichiometry to answer part a.
But wait! Which number do we do stoich with: 0.00200 or 0.00120🤔?
This is where the limiting reactant (LR) comes into play. The limiting reactant in a reaction is the substance that limits the amount of products produced. Basically, there are different amounts of each reactant. One reactant is more abundant, right?
The reactant that there is less of eventually stops the reaction and limits it since the reactant runs out. The other reactant is called the excess since there is still some of it left over, unreacted.
To find the LR, we have to do stoichiometry with both amounts. Convert each reactant into the precipitate:
Since there are less moles of PbCl₂ using NaCl as a reactant, NaCl is the LR. Pb(C₂H₃O₂)₂ is the excess.
Now we know how many moles of NaCl, Pb(C₂H₃O₂)₂, and PbCl₂ we have, wecan answer part a for real now!🥳
0.00100 mol PbCl₂ x 278.2 g/mol = 0.278 g of PbCl₂
Step #5
Yay, we did half the problem! Let's move on to solving for the concentrations of ions. In order for us to do this, we have to know the moles of each ion and the volumes of each ion.
Let's think this through conceptually a bit. After PbCl₂ (s) forms, what is left in the solution?
Looking back at the LR, either Na⁺ or Cl⁻ will have a final concentration of 0 since one of them will be completely used up. Since Cl⁻ is in the precipitate, Cl⁻ has a final concentration of 0. All of the chloride anions in the solution have been used up to form as much precipitate as possible.
That was easy! 1/4 of part b is complete. 😊
The ion that is in the LR and precipitate ALWAYS has a final concentration of 0. Think of it as being 100% used up, so there is none of it left.
Step #6
In this next step, we can solve for the concentrations of two ions: Na⁺ and C₂H₃O₂. These are considered spectator ions since they aren't in the precipitate. To find their concentrations, we have to use both the 0.00100 mol of PbCl₂ from using NaCl and the 0.00120 mol of PCl₂ from using Pb(C₂H₃O₂)₂.
The first number can help us find Na⁺ whereas the second can help us find C₂H₃O₂⁻.
Na+: All you have to do now is find the volume, but we have to multiply the number of moles by 2 since NaCl has an initial coefficient of 2. This is where balancing the reaction comes in! To find the volume, we just have to add 20.0 mL and 30.0 mL and convert to liters.
(0.00100)(2) / 0.050 L = 0.0400 M of Na⁺
C₂H₃O₂⁻: We have to multiply by 2 here as well since there was a subscript on the reactant side of the equation.
(0.00120)(2) / 0.050 L = 0.0480 M of C₂H₃O₂⁻
Step #7
We have one last ion we have to calculate the concentration of: Pb⁺². This is slightly harder to find, but with some practice, you got this! 😌
To find the excess amount of lead, convert the LR to the soluble product. Here, we would convert 0.00200 moles of NaCl to find the moles reacted. Since there is a 1:2 mole ratio, 0.00100 moles reacted. Then, we would subtract by the excess number of moles (found in step 4), which is 0.00120.
0.00120 - 0.00100 = 0.00020 moles of Pb⁺² unreacted. Then we just divide by the volume in liters, so 0.00020 moles / 0.050 L = 0.0040 M of Pb⁺².
Final Answers
Part a: 0.278 g of PbCl₂
Part b: [Cl⁻] = 0
[Na⁺] = 0.0400
[C₂H₃O₂⁻] = 0.0480
[Pb⁺²] = 0.0040
This is a very difficult question but once you practice and understand it conceptually, you'll begin to be able to get through it faster. It is honestly a lot in one question and probably won't be tested like this. However, knowing it will strengthen your overall stoichiometry skills, so it doesn't hurt! 🙃

© 2025 Fiveable Inc. All rights reserved.