Browse By Unit
Dylan Black
Dalia Savy
Dylan Black
Dalia Savy
In chemistry, when discussing kinetics, we know that when the concentration of a reactant rises, the rate of the reaction similarly increases. This makes sense since it logically follows that if we have more reactants in the same volume compared to a lesser amount of reactant, there will be a quicker reaction. However, how do we quantitatively determine how much faster the rate will be? Well, this is where a rate law comes into play.
👉Be sure to review reaction rates and factors that influence it, such as concentration as we spoke about here.
What is a Rate Law?
In chemistry, a rate law is an equation that describes the relationship between the rate of a chemical reaction and the concentrations of the reactants. A rate law is defined by saying: R = k[A]^n[B]^m... where:
- R is the rate of the reaction (sometimes also notated as Δ[]/Δt, which we will delve more in-depth into in the next section),
- k is the rate constant,
- [A] and [B] represent the concentrations of reactants, and
- n and m are reaction orders for each reactant (A, B, etc). This rate law is generalized, which is why there is a ... following. A reaction could hypothetically have 3, 4, or 5 reactants, though for the AP exam you often won't see more than 2. It's actually quite rare for a reaction with 3+ reactants since it would require three atoms/molecules to bump into each other just right for a reaction to take place. It occurs, but not often and not quickly.
Animation Courtesy of GIPHY; We'll delve deeper into collisions later in this unit.
What Does Reaction Order Mean?
n and m define what is called each reactant's reaction order. Reaction order brings us back to the initial question we asked: how do we determine quantitatively how concentration changes the rate of reaction? The reaction order is the answer! It describes how the rate of the reaction changes as the concentration of each reactant changes.
For example, let's say the imaginary rate law for the reaction A + B → C is R = k[A]²[B]¹. This can tell us that as we increase the concentration of A (assuming a constant [B]), the rate will increase quadratically. For example, if we double the concentration of A, the rate will quadruple. Similarly, if we double the concentration of B, the rate will double, since the order of B is 1. The same applies for orders of 3, 4, etc. (if we double [], R goes up by 8 times and 16 times respectively).
The overall reaction order for the full reaction is the sum of the orders for each reactant. In our imaginary example, the overall reaction order would be 3, since the reaction order of reactant A is 2 and the reaction order of reactant B is 1.
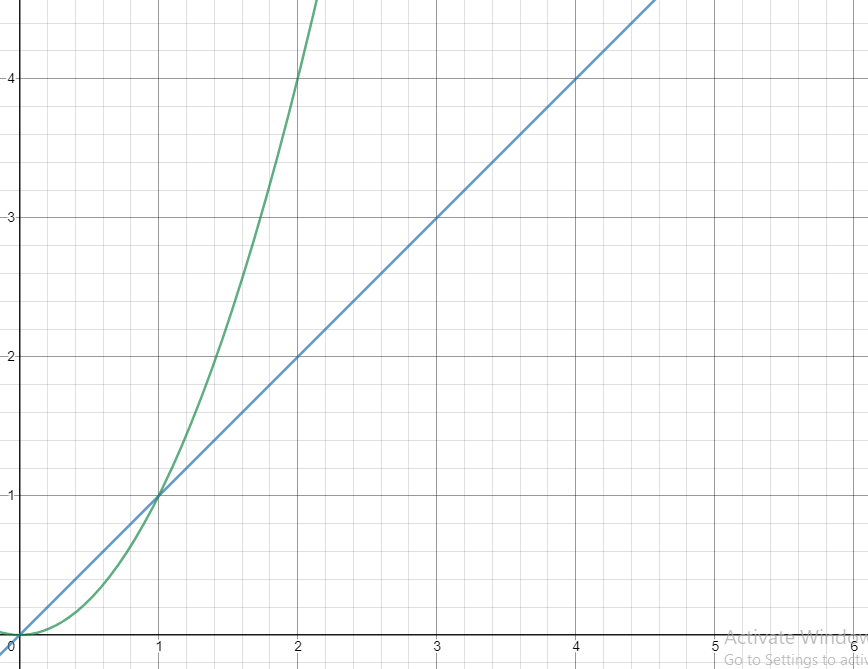
Quadratic vs. Linear Relationships (x^2 vs x)
Using Experiments to Determine a Rate Law
There's one important thing to note about rate laws: they can only be determined experimentally. What a chemist will do is run a ton of tests at different concentrations and then find the corresponding rates for each test. With this data, they can determine the rate of the reaction. Let's take a look at an example to find out how we mathematically figure this out:
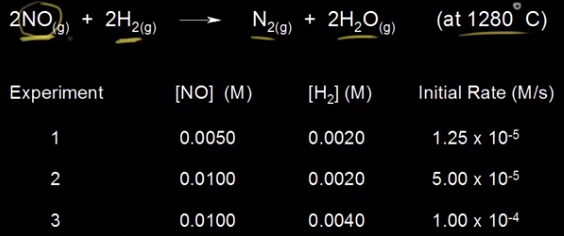
Example Courtesy of Khan Academy
Here we have a reaction: 2NO + 2H₂ → N₂ + 2H₂O. We can see three experiments done with different concentrations for each reactant. Let's take a look at the first two experiments where [NO] changes. We see the concentration of [NO] double from the first experiment to the second, and then we see the rate increase from 1.25 * 10⁻⁵ to 5.00 * 10⁻⁵. This is a change by a factor of 4 (5 * 10⁻⁵/1.25 * 10⁻⁵ = 4). Therefore, since doubling concentration makes the rate quadruple, the reaction is 2nd order with regard to NO. Note that in order to find the reaction order with respect to NO, we had to choose two experiments where the [NO] changed, but [H₂] was constant.
Let's take a look at H₂ now. For experiments 2 and 3, the concentration of H₂ doubles like it did for NO, but the rate increases from 5 * 10⁻⁵ to 1 * 10⁻⁴, by a factor of 2 (1 * 10⁻⁴/⁵ * 10⁻⁵ = 2). Therefore, the reaction is first order in H₂. Now, we can put together the rate law by putting all of this together: R = k[NO]²[H₂]. As an exercise, pick one of the experiments and plug in the correct numbers to figure out the value of k, and then read the next section and figure out the right units for k. (You should get k = 250 M⁻²s⁻¹).
If you were to assume the reaction orders just by looking at the chemical equation, you'd get a rate law of R = k[NO]²[H₂]². This is why it is important to use experimental data to write the correct rate law: R = k[NO]²[H₂].
Understanding k, the Rate Constant
The rate constant, k, is a tricky thing to understand. Essentially, it serves as a proportionality constant for the reaction to take place. It makes a bit more sense if you understand the calculus behind kinetics (which we will describe in the next section, though it is by no means required for the AP exam), but essentially all you need to know is that k is a constant that quantifies the rate of each reaction and that it is temperature specific. This means that for the same reaction at different temperatures, the rate constant is different!
Another important aspect of the rate constant is that its units change depending on the overall reaction order. Let's see if we can figure some of them out. Rate is always in M/s, and concentration is always in M (M = mol/L). Thus it follows that for certain reactions:
Zeroth Order
If the overall reaction order is 0:
- The rate law is R = k[A]⁰, which simplfies to R = k
- k is in units M/s.
First Order
If the overall reaction order is 1:
- R = k[A]¹, which you can think of as M/s = k * M
- k is in s⁻¹ (per seconds)
Second Order
If the overall reaction order is 2:
- R = k[A]², which you can think of as M/s = k * M²
- k is in M⁻¹*s⁻¹ (1/Ms) 🎥 Watch AP Chemistry teacher Mónica Gracida review reaction rates and rate laws in unit five of AP Chemistry: Kinetics.
<< Hide Menu
Dylan Black
Dalia Savy
Dylan Black
Dalia Savy
In chemistry, when discussing kinetics, we know that when the concentration of a reactant rises, the rate of the reaction similarly increases. This makes sense since it logically follows that if we have more reactants in the same volume compared to a lesser amount of reactant, there will be a quicker reaction. However, how do we quantitatively determine how much faster the rate will be? Well, this is where a rate law comes into play.
👉Be sure to review reaction rates and factors that influence it, such as concentration as we spoke about here.
What is a Rate Law?
In chemistry, a rate law is an equation that describes the relationship between the rate of a chemical reaction and the concentrations of the reactants. A rate law is defined by saying: R = k[A]^n[B]^m... where:
- R is the rate of the reaction (sometimes also notated as Δ[]/Δt, which we will delve more in-depth into in the next section),
- k is the rate constant,
- [A] and [B] represent the concentrations of reactants, and
- n and m are reaction orders for each reactant (A, B, etc). This rate law is generalized, which is why there is a ... following. A reaction could hypothetically have 3, 4, or 5 reactants, though for the AP exam you often won't see more than 2. It's actually quite rare for a reaction with 3+ reactants since it would require three atoms/molecules to bump into each other just right for a reaction to take place. It occurs, but not often and not quickly.

Animation Courtesy of GIPHY; We'll delve deeper into collisions later in this unit.
What Does Reaction Order Mean?
n and m define what is called each reactant's reaction order. Reaction order brings us back to the initial question we asked: how do we determine quantitatively how concentration changes the rate of reaction? The reaction order is the answer! It describes how the rate of the reaction changes as the concentration of each reactant changes.
For example, let's say the imaginary rate law for the reaction A + B → C is R = k[A]²[B]¹. This can tell us that as we increase the concentration of A (assuming a constant [B]), the rate will increase quadratically. For example, if we double the concentration of A, the rate will quadruple. Similarly, if we double the concentration of B, the rate will double, since the order of B is 1. The same applies for orders of 3, 4, etc. (if we double [], R goes up by 8 times and 16 times respectively).
The overall reaction order for the full reaction is the sum of the orders for each reactant. In our imaginary example, the overall reaction order would be 3, since the reaction order of reactant A is 2 and the reaction order of reactant B is 1.

Quadratic vs. Linear Relationships (x^2 vs x)
Using Experiments to Determine a Rate Law
There's one important thing to note about rate laws: they can only be determined experimentally. What a chemist will do is run a ton of tests at different concentrations and then find the corresponding rates for each test. With this data, they can determine the rate of the reaction. Let's take a look at an example to find out how we mathematically figure this out:

Example Courtesy of Khan Academy
Here we have a reaction: 2NO + 2H₂ → N₂ + 2H₂O. We can see three experiments done with different concentrations for each reactant. Let's take a look at the first two experiments where [NO] changes. We see the concentration of [NO] double from the first experiment to the second, and then we see the rate increase from 1.25 * 10⁻⁵ to 5.00 * 10⁻⁵. This is a change by a factor of 4 (5 * 10⁻⁵/1.25 * 10⁻⁵ = 4). Therefore, since doubling concentration makes the rate quadruple, the reaction is 2nd order with regard to NO. Note that in order to find the reaction order with respect to NO, we had to choose two experiments where the [NO] changed, but [H₂] was constant.
Let's take a look at H₂ now. For experiments 2 and 3, the concentration of H₂ doubles like it did for NO, but the rate increases from 5 * 10⁻⁵ to 1 * 10⁻⁴, by a factor of 2 (1 * 10⁻⁴/⁵ * 10⁻⁵ = 2). Therefore, the reaction is first order in H₂. Now, we can put together the rate law by putting all of this together: R = k[NO]²[H₂]. As an exercise, pick one of the experiments and plug in the correct numbers to figure out the value of k, and then read the next section and figure out the right units for k. (You should get k = 250 M⁻²s⁻¹).
If you were to assume the reaction orders just by looking at the chemical equation, you'd get a rate law of R = k[NO]²[H₂]². This is why it is important to use experimental data to write the correct rate law: R = k[NO]²[H₂].
Understanding k, the Rate Constant
The rate constant, k, is a tricky thing to understand. Essentially, it serves as a proportionality constant for the reaction to take place. It makes a bit more sense if you understand the calculus behind kinetics (which we will describe in the next section, though it is by no means required for the AP exam), but essentially all you need to know is that k is a constant that quantifies the rate of each reaction and that it is temperature specific. This means that for the same reaction at different temperatures, the rate constant is different!
Another important aspect of the rate constant is that its units change depending on the overall reaction order. Let's see if we can figure some of them out. Rate is always in M/s, and concentration is always in M (M = mol/L). Thus it follows that for certain reactions:
Zeroth Order
If the overall reaction order is 0:
- The rate law is R = k[A]⁰, which simplfies to R = k
- k is in units M/s.
First Order
If the overall reaction order is 1:
- R = k[A]¹, which you can think of as M/s = k * M
- k is in s⁻¹ (per seconds)
Second Order
If the overall reaction order is 2:
- R = k[A]², which you can think of as M/s = k * M²
- k is in M⁻¹*s⁻¹ (1/Ms) 🎥 Watch AP Chemistry teacher Mónica Gracida review reaction rates and rate laws in unit five of AP Chemistry: Kinetics.

© 2025 Fiveable Inc. All rights reserved.