Browse By Unit
Dylan Black
Jillian Holbrook
Dylan Black
Jillian Holbrook
Now that we understand equilibrium with acids and bases, it is time to get into the fun stuff: mixing acids and bases together! In this section, we introduce the idea of reactions between acids and bases, such as the reaction CH3COOH + NaOH → CH3COONa + H2O, and how it relates to a new topic: buffers.
Defining Buffers
Buffers are awesome. Buffers are a mixture of an acid (HA) and its conjugate base (A-) in a solution. What makes a buffer interesting is that it is resistant to changes in pH. When adding some acid or base to a buffer, you will find that the pH (for a range) will not change much. Why? If you add acid, the conjugate base will take care of it, and vice versa.
Buffers are important both in chemistry and biology. Buffers are found everywhere in organisms to maintain homeostasis, a healthy state. In fact, your own blood is a buffer! 🩸
Buffers are incredibly important not only because of their biological ramifications but also in their creation via chemical reactions between acids and bases.

Reactions with Acids and Bases
Strong Acid Strong Base Reactions
A strong acid strong base reaction is one that you are most likely familiar with. This is the type of acid-base reaction students see in Unit 4 when acids and bases are first introduced without the ✨magic✨ of equilibrium.
An example of a strong acid strong base equilibrium is the reaction between HCl and NaOH to form NaCl and H2O. However, when we look closer, we find that for this reaction (and any strong acid strong base reaction), the ions are spectators, so the net ionic is just H+ + OH- <=> H2O.
Take a look at an example problem with a strong acid strong base reaction:
What is the pH after the addition of 10.0 mL of 0.100 M NaOH to 25.0 mL of 0.100 M HCl?
Start by writing out our reaction:
HCl + NaOH <=> NaCl + H2O
Writing the net ionic, we find that Cl- and Na+ are spectators, giving us:
H+ + OH- <=> H2O
By multiplying mL times molarity, we can find the number of millimoles of each species:
10.0 * 0.1 = 1mmol OH-
25.0 * 0.1 = 2.5mmol H+
We use stoichiometry to find how much H+ is left over (we know that all of the OH- will be used up because H+ is in excess).
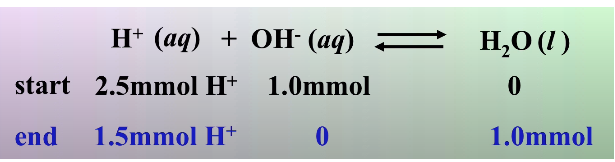
Finally, we divide 1.5mmol H+ by the volume (35mL) to find [H+] = 4.8 * 10^-2, which corresponds to a pH of 1.37.
It is worth noting that with strong acid strong base reactions (and other reactions we will discuss), that there are three "zones": the zone where the acid is in excess, where the base is in excess, or where the two are equimolar. This thinking will come in handy when we apply these reactions in the next section about titrations.
Weak Acid Strong Base Reactions
Weak acid strong base reactions are very similar to strong acid strong base reactions, except the acid does not fully dissociate, meaning our net ionic equation will be slightly different. For the example in this section, we will use the reaction CH3COOH + NaOH <=> CH3COONa + H2O.
Like before, we see that Na+ is a spectator. However, we cannot say the same about CH3COO- because CH3COOH is a weak acid and does not fully dissociate. Our net ionic equation for this reaction will be CH3COOH + OH- <=> CH3COO- + H2O, which we will use for calculations.
In general, you usually want to start problems with acid-base reactions by writing out the net ionic equation. With these problems, we are going to start seeing buffers, mixtures of an acid and its conjugate base. We will discuss calculating the pH of these buffers in detail, but for now, just know that we can use this equation:

Let's take a look at an example!
Calculate the pH in the titration of 25.0 mL of 0.100 M acetic acid with 0.100 M NaOH after adding 10.00 mL of 0.100 M NaOH.
We can use the same procedure for solving our strong acid strong base problem for this problem. First, calculate millimoles, and then use stoichiometry to find what's left.

However, what's different here is that instead of having H+ or OH- at the end, we have a mixture of CH3COOH and its conjugate base CH3COO-. We can use the above equation to solve for pH:

Note that the equation calls for concentrations of the conjugate base and the acid. Because we have the same volume of each, the divisions would cancel out.
Again, like the strong acid strong base reaction, you will have points with only acid, a buffer region (this is unique to weak acid/base reactions), an equivalence point (where mmol acid = mmol base), and a post-equivalence region.
The strategies shown in this example can be applied to weak base strong acid reactions. Just remember to be careful about managing conjugate acids/bases and distinguishing between pH or pOH. On the AP Exam, a weak acid strong base example is much more likely, but be ready for either.
<< Hide Menu
Dylan Black
Jillian Holbrook
Dylan Black
Jillian Holbrook
Now that we understand equilibrium with acids and bases, it is time to get into the fun stuff: mixing acids and bases together! In this section, we introduce the idea of reactions between acids and bases, such as the reaction CH3COOH + NaOH → CH3COONa + H2O, and how it relates to a new topic: buffers.
Defining Buffers
Buffers are awesome. Buffers are a mixture of an acid (HA) and its conjugate base (A-) in a solution. What makes a buffer interesting is that it is resistant to changes in pH. When adding some acid or base to a buffer, you will find that the pH (for a range) will not change much. Why? If you add acid, the conjugate base will take care of it, and vice versa.
Buffers are important both in chemistry and biology. Buffers are found everywhere in organisms to maintain homeostasis, a healthy state. In fact, your own blood is a buffer! 🩸
Buffers are incredibly important not only because of their biological ramifications but also in their creation via chemical reactions between acids and bases.

Reactions with Acids and Bases
Strong Acid Strong Base Reactions
A strong acid strong base reaction is one that you are most likely familiar with. This is the type of acid-base reaction students see in Unit 4 when acids and bases are first introduced without the ✨magic✨ of equilibrium.
An example of a strong acid strong base equilibrium is the reaction between HCl and NaOH to form NaCl and H2O. However, when we look closer, we find that for this reaction (and any strong acid strong base reaction), the ions are spectators, so the net ionic is just H+ + OH- <=> H2O.
Take a look at an example problem with a strong acid strong base reaction:
What is the pH after the addition of 10.0 mL of 0.100 M NaOH to 25.0 mL of 0.100 M HCl?
Start by writing out our reaction:
HCl + NaOH <=> NaCl + H2O
Writing the net ionic, we find that Cl- and Na+ are spectators, giving us:
H+ + OH- <=> H2O
By multiplying mL times molarity, we can find the number of millimoles of each species:
10.0 * 0.1 = 1mmol OH-
25.0 * 0.1 = 2.5mmol H+
We use stoichiometry to find how much H+ is left over (we know that all of the OH- will be used up because H+ is in excess).

Finally, we divide 1.5mmol H+ by the volume (35mL) to find [H+] = 4.8 * 10^-2, which corresponds to a pH of 1.37.
It is worth noting that with strong acid strong base reactions (and other reactions we will discuss), that there are three "zones": the zone where the acid is in excess, where the base is in excess, or where the two are equimolar. This thinking will come in handy when we apply these reactions in the next section about titrations.
Weak Acid Strong Base Reactions
Weak acid strong base reactions are very similar to strong acid strong base reactions, except the acid does not fully dissociate, meaning our net ionic equation will be slightly different. For the example in this section, we will use the reaction CH3COOH + NaOH <=> CH3COONa + H2O.
Like before, we see that Na+ is a spectator. However, we cannot say the same about CH3COO- because CH3COOH is a weak acid and does not fully dissociate. Our net ionic equation for this reaction will be CH3COOH + OH- <=> CH3COO- + H2O, which we will use for calculations.
In general, you usually want to start problems with acid-base reactions by writing out the net ionic equation. With these problems, we are going to start seeing buffers, mixtures of an acid and its conjugate base. We will discuss calculating the pH of these buffers in detail, but for now, just know that we can use this equation:

Let's take a look at an example!
Calculate the pH in the titration of 25.0 mL of 0.100 M acetic acid with 0.100 M NaOH after adding 10.00 mL of 0.100 M NaOH.
We can use the same procedure for solving our strong acid strong base problem for this problem. First, calculate millimoles, and then use stoichiometry to find what's left.

However, what's different here is that instead of having H+ or OH- at the end, we have a mixture of CH3COOH and its conjugate base CH3COO-. We can use the above equation to solve for pH:

Note that the equation calls for concentrations of the conjugate base and the acid. Because we have the same volume of each, the divisions would cancel out.
Again, like the strong acid strong base reaction, you will have points with only acid, a buffer region (this is unique to weak acid/base reactions), an equivalence point (where mmol acid = mmol base), and a post-equivalence region.
The strategies shown in this example can be applied to weak base strong acid reactions. Just remember to be careful about managing conjugate acids/bases and distinguishing between pH or pOH. On the AP Exam, a weak acid strong base example is much more likely, but be ready for either.

© 2025 Fiveable Inc. All rights reserved.