Browse By Unit
Dylan Black
Jillian Holbrook
Dylan Black
Jillian Holbrook
Time for most AP Chemistry students' least favorite topic: acid-base titrations. However, acid-base titrations are not as hard as they seem! Acid-base titrations combine all of the skills we have seen so far in Unit 8: equilibrium, pH, pKas, and even some stoichiometry just for funsies.
First, let's enjoy a quick blast from the past to Unit 4 and examine what titrations are.
What is a Titration?
A titration is a lab procedure taken to find the concentration of an unknown "analyte," also known as the "titrand". Using a burette, small amounts of the titrant, a solution of known concentration, are dripped into the analyte until we hit the equivalence point.
The equivalence point is the point at which the mols of analyte present are equal to the mols of titrant that have been dripped. This can be represented mathematically by saying nMaVa = mMbVb, where n and m are stoichiometric coefficients and M and V are the molarities and volumes of the analyte and titrant at the equivalence point.
Titrations are often used to calculate the concentration of an acid in solution because acids and bases respond so well to each other, especially when in combination with an acid-base indicator. The following diagram shows what an acid-base titration (or any titration for what it's worth) looks like:
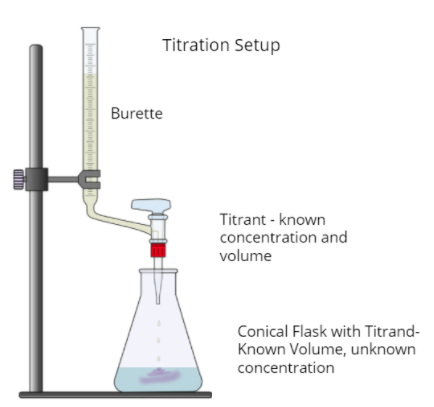
Titration Curves
As an acid or base is dripped into a base or acid of unknown concentration, we can keep track of the pH as we add more and more of the titrant.
Let's look at an example of what happens as we drip 1M NaOH into 25 mL of 1M HCl:
Pre-Titration
Our first step is to take a pH reading before any titrant has been added. For this example, we have an HCl concentration of 1M, meaning the pH is -log([1]) = 0.
Pre-Equivalence Point
As we add in NaOH, the following net ionic equation occurs:
H+ + OH- <=> H2O
If we add OH- up until the equivalence point, we will have an excess of H+. This means that our solution will still have exclusively H+, but to a lesser degree, because some of the original H+ will create H2O. Therefore, up until the equivalence point, our pH will slowly increase.
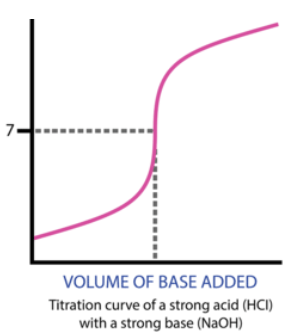
The graph below indicates a slow increase in pH on the y-axis as mL of NaOH are added along the x-axis:
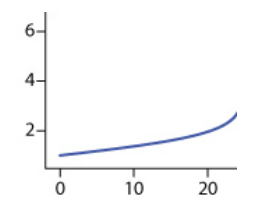
Equivalence Point
Then, we reach a turning point where the moles of HCl originally in the solution (25mmol) will equal the moles of NaOH added. This occurs at 25mL (we know this by solving the equation MaVa = MbVb). At 25mL, we have 25mmol of both HCl and NaOH, meaning we have no excess reactant and are left over with only water at the end.
At the equivalence point, our pH is 7. This is true of any titration between a strong acid and a strong base. (We will get to weak acids and bases later).
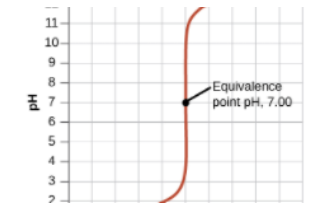
Post-Equivalence Point
Once we reach past the equivalence point, we will have an excess of base, indicating that our pH slowly increases as we add more base, similarly to before the equivalence point.
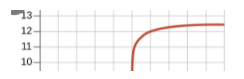
Overall, here is what the titration curve for this entire titration looks like:
Titrations with Weak Acids and Bases
The minor problem with our example above is that most acids and bases are not strong! However, the process is almost exactly the same when we have a strong acid and a weak base or a strong base and a weak acid (the latter is more common to see on the AP Exam).
One subtle difference is that before you reach the equivalence point, you will have both acid and conjugate base (or base and conjugate acid) in the solution! What alarms should this be setting off? 🚨 BUFFER!!! 🚨 In the net ionic equation, we still have both the weak acid and the conjugate base because it does not fully dissociate.
Take, for example, the titration of NaOH into acetic acid:
CH3COOH + NaOH <=> CH3COONa + H2O
CH3COOH + OH- <=> CH3COO- + H2O
When we have an excess in CH3COOH, we end up with both CH3COOH and CH3COO-. A buffer! The same goes for the opposite situation (for example, the titration of HCl into NH4NO3). Thus, our solution is less responsive to changes in pH and will have a half-equivalence point at exactly 1/2 the volume of the equivalence point. At this point, we have the maximum buffer where pH=pKa or pOH=pKb (If you're titrating a weak acid with a strong base, use the former, and vice versa).
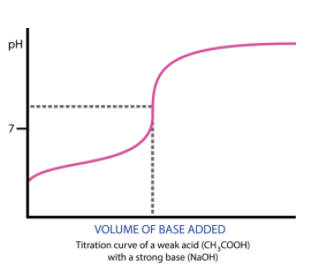
Furthermore, because there is a product other than H2O, the pH at the equivalence point will not always be 7! In fact, it will never be 7. When titrating a weak base with a strong acid, your equivalence point will be acidic, and vice versa, a weak acid with a strong base will yield a basic equivalence point. This is because, at the equivalence point, you will create some conjugate base/acid.
See an example of two titration curves, one with a strong base and weak acid and the other with a strong acid and weak base. Test yourself on whether you can find the half-equivalence point and equivalence point and estimate what the pH at the equivalence point is and the Ka/Kb of the acid/base!
Reading a Burette
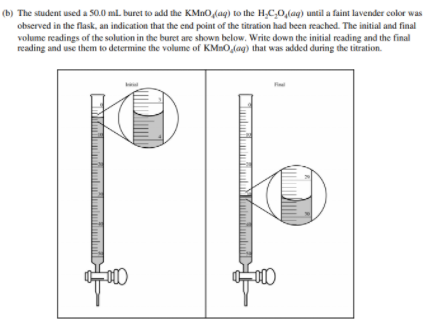
Before we get to some examples, take a quick detour to learn how to read a burette. When doing a titration, this is an essential skill, as it allows you to see how much titrant you have added to the analyte.
Let's go through an example FRQ:
Example Problems
Finding Molarity at the Equivalence Point
Find the concentration of HF at the equivalence point when titrating HF with NaOH if the equivalence point occurs when 20mL of 0.1M NaOH is titrated into 10mL HF.
For this problem, we can use our equation MaVa = MbVb, which describes how at the equivalence point we have equimolar quantities of titrant and analyte:
Ma(10mL) = (0.1M)(20mL)
Ma = (0.1)(20)/10 = 0.2M
Therefore, the concentration of HF is 0.2M. Similar strategies can be used to find volumes at the equivalence point!
Weak Acid/Strong Base Titration
Find the pH of the solution formed from the titration of 25mL of 0.1M CH3COOH with 10mL 0.1M KOH (Ka = 1.8 * 10^-5)
Let's start by writing out our reaction and finding our net ionic:
CH3COOH + KOH <=> CH3COOK + H2O
CH3COOH + OH- <=> CH3COO- + H2O
Next, we find mmol and do the stoichiometry dance:
25 * 0.1 = 2.5mmol CH3COOH
10 * 0.1 = 1.0mmol OH-
CH3COOH + OH- <=> CH3COO- + H2O
2.5mmol 1.0mmol 0 0
1.5mmol 0mmol 1.0mmol 1.0mmol
Finally, we can use the Henderson-Hasselbalch equation to find the pH:
pH = pKa + log(1.0/1.5) = 4.74 + log(1/1.5) = 4.56
Weak Base/Strong Acid Titration
The process with a weak base strong acid titration is essentially the same:
Find the pH of the solution formed from the titration of 30mL of 0.5M NH3 with 10mL 0.1M HCl (Kb = 1.8 * 10^-5)
First, let's write out our net ionic:
NH3 + HCl <=> NH4Cl
NH3 + H+ <=> NH4+
Next, we find mmols and do stoichiometry:
30mL * 0.5M = 15mmol NH3
10mL * 0.1M = 1mmol HCl
NH3 + H+ <=> NH4+
15mmol 1mmol 0mmol
14mmol 0mmol 1mmol
Finally, use the Henderson-Hasselbalch for bases to find the pOH:
pOH = pKb + log(1/14) = 4.74 + log(1/14) = 3.59
Subtract from 14 to find that pH = 10.41.
<< Hide Menu
Dylan Black
Jillian Holbrook
Dylan Black
Jillian Holbrook
Time for most AP Chemistry students' least favorite topic: acid-base titrations. However, acid-base titrations are not as hard as they seem! Acid-base titrations combine all of the skills we have seen so far in Unit 8: equilibrium, pH, pKas, and even some stoichiometry just for funsies.
First, let's enjoy a quick blast from the past to Unit 4 and examine what titrations are.
What is a Titration?
A titration is a lab procedure taken to find the concentration of an unknown "analyte," also known as the "titrand". Using a burette, small amounts of the titrant, a solution of known concentration, are dripped into the analyte until we hit the equivalence point.
The equivalence point is the point at which the mols of analyte present are equal to the mols of titrant that have been dripped. This can be represented mathematically by saying nMaVa = mMbVb, where n and m are stoichiometric coefficients and M and V are the molarities and volumes of the analyte and titrant at the equivalence point.
Titrations are often used to calculate the concentration of an acid in solution because acids and bases respond so well to each other, especially when in combination with an acid-base indicator. The following diagram shows what an acid-base titration (or any titration for what it's worth) looks like:

Titration Curves
As an acid or base is dripped into a base or acid of unknown concentration, we can keep track of the pH as we add more and more of the titrant.
Let's look at an example of what happens as we drip 1M NaOH into 25 mL of 1M HCl:
Pre-Titration
Our first step is to take a pH reading before any titrant has been added. For this example, we have an HCl concentration of 1M, meaning the pH is -log([1]) = 0.
Pre-Equivalence Point
As we add in NaOH, the following net ionic equation occurs:
H+ + OH- <=> H2O
If we add OH- up until the equivalence point, we will have an excess of H+. This means that our solution will still have exclusively H+, but to a lesser degree, because some of the original H+ will create H2O. Therefore, up until the equivalence point, our pH will slowly increase.
The graph below indicates a slow increase in pH on the y-axis as mL of NaOH are added along the x-axis:

Equivalence Point
Then, we reach a turning point where the moles of HCl originally in the solution (25mmol) will equal the moles of NaOH added. This occurs at 25mL (we know this by solving the equation MaVa = MbVb). At 25mL, we have 25mmol of both HCl and NaOH, meaning we have no excess reactant and are left over with only water at the end.
At the equivalence point, our pH is 7. This is true of any titration between a strong acid and a strong base. (We will get to weak acids and bases later).

Post-Equivalence Point
Once we reach past the equivalence point, we will have an excess of base, indicating that our pH slowly increases as we add more base, similarly to before the equivalence point.

Overall, here is what the titration curve for this entire titration looks like:

Titrations with Weak Acids and Bases
The minor problem with our example above is that most acids and bases are not strong! However, the process is almost exactly the same when we have a strong acid and a weak base or a strong base and a weak acid (the latter is more common to see on the AP Exam).
One subtle difference is that before you reach the equivalence point, you will have both acid and conjugate base (or base and conjugate acid) in the solution! What alarms should this be setting off? 🚨 BUFFER!!! 🚨 In the net ionic equation, we still have both the weak acid and the conjugate base because it does not fully dissociate.
Take, for example, the titration of NaOH into acetic acid:
CH3COOH + NaOH <=> CH3COONa + H2O
CH3COOH + OH- <=> CH3COO- + H2O
When we have an excess in CH3COOH, we end up with both CH3COOH and CH3COO-. A buffer! The same goes for the opposite situation (for example, the titration of HCl into NH4NO3). Thus, our solution is less responsive to changes in pH and will have a half-equivalence point at exactly 1/2 the volume of the equivalence point. At this point, we have the maximum buffer where pH=pKa or pOH=pKb (If you're titrating a weak acid with a strong base, use the former, and vice versa).
Furthermore, because there is a product other than H2O, the pH at the equivalence point will not always be 7! In fact, it will never be 7. When titrating a weak base with a strong acid, your equivalence point will be acidic, and vice versa, a weak acid with a strong base will yield a basic equivalence point. This is because, at the equivalence point, you will create some conjugate base/acid.
See an example of two titration curves, one with a strong base and weak acid and the other with a strong acid and weak base. Test yourself on whether you can find the half-equivalence point and equivalence point and estimate what the pH at the equivalence point is and the Ka/Kb of the acid/base!


Reading a Burette
Before we get to some examples, take a quick detour to learn how to read a burette. When doing a titration, this is an essential skill, as it allows you to see how much titrant you have added to the analyte.
Let's go through an example FRQ:

Example Problems
Finding Molarity at the Equivalence Point
Find the concentration of HF at the equivalence point when titrating HF with NaOH if the equivalence point occurs when 20mL of 0.1M NaOH is titrated into 10mL HF.
For this problem, we can use our equation MaVa = MbVb, which describes how at the equivalence point we have equimolar quantities of titrant and analyte:
Ma(10mL) = (0.1M)(20mL)
Ma = (0.1)(20)/10 = 0.2M
Therefore, the concentration of HF is 0.2M. Similar strategies can be used to find volumes at the equivalence point!
Weak Acid/Strong Base Titration
Find the pH of the solution formed from the titration of 25mL of 0.1M CH3COOH with 10mL 0.1M KOH (Ka = 1.8 * 10^-5)
Let's start by writing out our reaction and finding our net ionic:
CH3COOH + KOH <=> CH3COOK + H2O
CH3COOH + OH- <=> CH3COO- + H2O
Next, we find mmol and do the stoichiometry dance:
25 * 0.1 = 2.5mmol CH3COOH
10 * 0.1 = 1.0mmol OH-
CH3COOH + OH- <=> CH3COO- + H2O
2.5mmol 1.0mmol 0 0
1.5mmol 0mmol 1.0mmol 1.0mmol
Finally, we can use the Henderson-Hasselbalch equation to find the pH:
pH = pKa + log(1.0/1.5) = 4.74 + log(1/1.5) = 4.56
Weak Base/Strong Acid Titration
The process with a weak base strong acid titration is essentially the same:
Find the pH of the solution formed from the titration of 30mL of 0.5M NH3 with 10mL 0.1M HCl (Kb = 1.8 * 10^-5)
First, let's write out our net ionic:
NH3 + HCl <=> NH4Cl
NH3 + H+ <=> NH4+
Next, we find mmols and do stoichiometry:
30mL * 0.5M = 15mmol NH3
10mL * 0.1M = 1mmol HCl
NH3 + H+ <=> NH4+
15mmol 1mmol 0mmol
14mmol 0mmol 1mmol
Finally, use the Henderson-Hasselbalch for bases to find the pOH:
pOH = pKb + log(1/14) = 4.74 + log(1/14) = 3.59
Subtract from 14 to find that pH = 10.41.

© 2025 Fiveable Inc. All rights reserved.