Browse By Unit
Dylan Black
Jillian Holbrook
Dylan Black
Jillian Holbrook
Introduction to the Henderson-Hasselbalch Equation
This section focuses intimately on one equation: the Henderson-Hasselbalch equation. The Henderson-Hasselbalch equation is useful because it helps us find the pH of a buffer. Thinking back to 8.8, a buffer is a solution that resists changes to its pH and is composed of a weak acid and its conjugate base or a weak base and its conjugate acid.
Let's take a look at the Henderson-Hasselbalch equation and get ourselves situated with it:
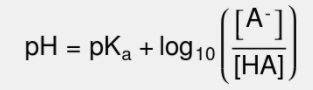
Breaking Down The Equation
Breaking the equation down, pH is the -log([H+]) and is oftentimes the unknown when we apply the Henderson-Hasselbalch Equation. pKa is -log(Ka) is a logarithmic scale to describe the acidity of an acid (lower pKa = more acidic). Finally, we get to the new bit, the log base 10 of the ratio of the concentrations of an ion, A-, and an acid HA. We can start by realizing that there is a unique relationship between [A-] and [HA]. They constitute a conjugate acid-base pair! HA is a weak acid, and A- is its conjugate base!
This is where the Henderson-Hasselbalch equation ties into buffers because you will always have a concentration of conjugate base and a concentration of conjugate acid. It also shows why the strongest buffer is when these concentrations are equal because then log([A-]/[HA]) = 0.
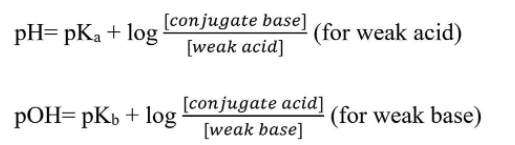
Two Forms of the Henderson-Hasselbalch Equation. Image from MicrobeNotes
Example Problems
Example Problem #1: Directly Stated Buffer
Find the pH of a buffer with 0.5M CH3COOH mixed with 0.25M CH3COONa (Ka = 1.8 * 10^-5).
For this, we can plug directly into the Henderson-Hasselbalch:
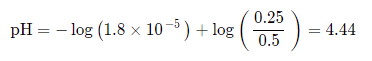
Example Problem #2: Using the Hasselbalch During A Titration
Calculate the pH in the titration of 25.0 mL of 0.100M acetic acid with 0.100M NaOH after adding 15.0 mL of 0.100M NaOH.
Start by writing out our net ionic equation for this reaction:
CH3COOH + NaOH <=> CH3COONa + H2O
CH3COOH + OH- <=> CH3COO- + H2O
Next, we can use stoichiometry to find how many mmol of each compound we have after the reaction goes forward:
CH3COOH + OH- <=> CH3COO- + H2O
Start: 2.5mmol CH3COOH, 1.5mmol OH-, 0mmol CH3COO-, 0mmol H2O
End: 2mmol CH3COOH, 0mmol OH-, 1.5mmol CH3COO-, 1.5mmol H2O
Because we have concentrations of both an acid and its conjugate base, we can find the pH of this by finding the pH of that buffer using the Henderson-Hasselbalch. Note that because we are dividing by the same volume to find concentration, they cancel out and we can just divide the mmols:
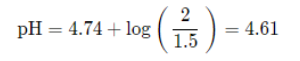
<< Hide Menu
Dylan Black
Jillian Holbrook
Dylan Black
Jillian Holbrook
Introduction to the Henderson-Hasselbalch Equation
This section focuses intimately on one equation: the Henderson-Hasselbalch equation. The Henderson-Hasselbalch equation is useful because it helps us find the pH of a buffer. Thinking back to 8.8, a buffer is a solution that resists changes to its pH and is composed of a weak acid and its conjugate base or a weak base and its conjugate acid.
Let's take a look at the Henderson-Hasselbalch equation and get ourselves situated with it:
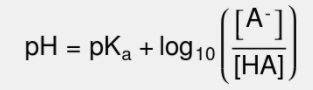
Breaking Down The Equation
Breaking the equation down, pH is the -log([H+]) and is oftentimes the unknown when we apply the Henderson-Hasselbalch Equation. pKa is -log(Ka) is a logarithmic scale to describe the acidity of an acid (lower pKa = more acidic). Finally, we get to the new bit, the log base 10 of the ratio of the concentrations of an ion, A-, and an acid HA. We can start by realizing that there is a unique relationship between [A-] and [HA]. They constitute a conjugate acid-base pair! HA is a weak acid, and A- is its conjugate base!
This is where the Henderson-Hasselbalch equation ties into buffers because you will always have a concentration of conjugate base and a concentration of conjugate acid. It also shows why the strongest buffer is when these concentrations are equal because then log([A-]/[HA]) = 0.

Two Forms of the Henderson-Hasselbalch Equation. Image from MicrobeNotes
Example Problems
Example Problem #1: Directly Stated Buffer
Find the pH of a buffer with 0.5M CH3COOH mixed with 0.25M CH3COONa (Ka = 1.8 * 10^-5).
For this, we can plug directly into the Henderson-Hasselbalch:
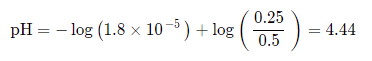
Example Problem #2: Using the Hasselbalch During A Titration
Calculate the pH in the titration of 25.0 mL of 0.100M acetic acid with 0.100M NaOH after adding 15.0 mL of 0.100M NaOH.
Start by writing out our net ionic equation for this reaction:
CH3COOH + NaOH <=> CH3COONa + H2O
CH3COOH + OH- <=> CH3COO- + H2O
Next, we can use stoichiometry to find how many mmol of each compound we have after the reaction goes forward:
CH3COOH + OH- <=> CH3COO- + H2O
Start: 2.5mmol CH3COOH, 1.5mmol OH-, 0mmol CH3COO-, 0mmol H2O
End: 2mmol CH3COOH, 0mmol OH-, 1.5mmol CH3COO-, 1.5mmol H2O
Because we have concentrations of both an acid and its conjugate base, we can find the pH of this by finding the pH of that buffer using the Henderson-Hasselbalch. Note that because we are dividing by the same volume to find concentration, they cancel out and we can just divide the mmols:
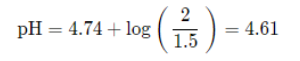

© 2025 Fiveable Inc. All rights reserved.