Browse By Unit
Jillian Holbrook
Jillian Holbrook
You made it to the last topic section of AP Chemistry. Before jumping in, congratulate yourself for making it this far! Over the AP Chem course, you have learned everything from acids and bases to equilibrium to thermodynamics.
For our final topic of Unit 9 and AP Chemistry, we will discuss nonspontaneous redox reactions and how we can use electrolytic cells to make them happen. This builds on the foundations of how electrolytic cells work, how we can differentiate galvanic (or voltaic) cells from electrolytic cells, and how to use Faraday's Law to make electrolysis calculations.
Review of Electrolytic Cells 🔋
As we learned in the introduction of galvanic and electrolytic cells, an electrolytic cell is a cell in which power from an external source (usually a battery) is used to spur nonspontaneous redox reactions by creating electromotive force. Electrolytic cells require energy because they are thermodynamically unfavorable, and therefore nonspontaneous. This means that a chemical species in an electrolytic reaction that would normally be oxidized is instead reduced and vice versa.
Take a look at an example of an electrolytic cell with Zinc and Copper:

Image From Abigail Giordano
In this image, we see that electrons are being pumped out of Cu to form Cu2+ and transferred to Zn2+ to form Zinc metal. The arrows show the direction of the electron flow, meaning the redox reaction occurring is: Cu + Zn2+ → Cu2+ + Zn.
By using a table of standard reduction potentials, we can calculate the cell potential, Ecell:
First, we write out our half-reactions:
Cu → Cu2+ + 2e- (E = -0.34 V)
Zn2+ + 2e- → Zn (E = -0.76 V)
Adding our E values, we find that Ecell = -1.10 V. Therefore, because of the negative voltage, we must introduce external power to cause the redox reaction to run.
Note on the battery in the cell diagram it must be a battery with a voltage of over 1.10 V. This is because the voltage must be enough to overcome the non-spontaneity of the redox reaction we want to occur (and also the spontaneousness of the reverse reaction which has an E value of +1.10 V). When we connect this battery, the voltage pulls electrons in the direction of the nonspontaneous reaction. Therefore, the mass of the copper electrode will decrease, and the mass of the zinc electrode will increase.
Comparing Electrolytic and Galvanic Cells
There are some important differences between a galvanic cell and an electrolytic cell that are necessary to know and recognize for the AP exam. Examine the following galvanic cell and electrolytic cell side by side:
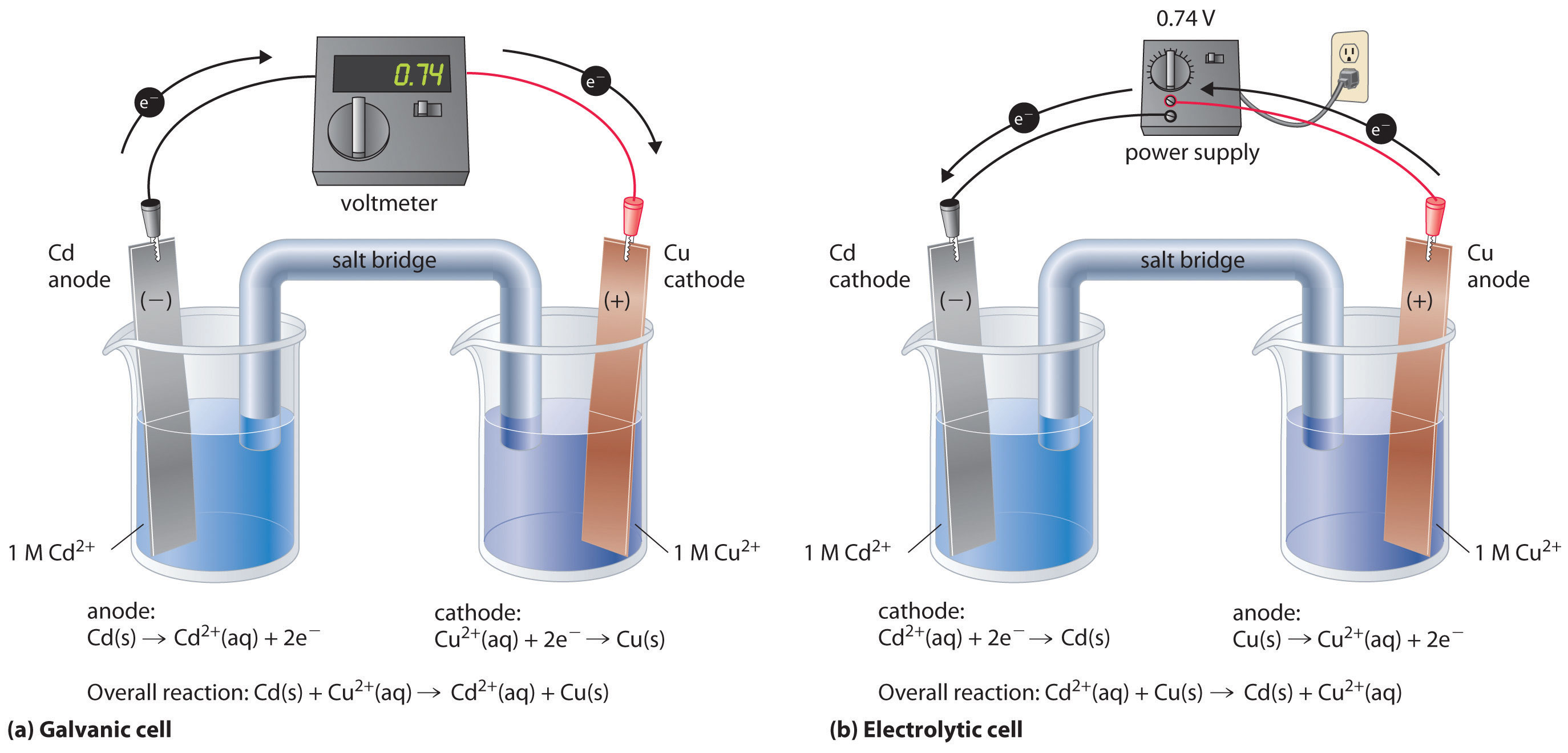
Image From LibreTexts
On the left, the galvanic cell has an anode where oxidation occurs and a cathode where reduction occurs. The reaction occurring is with cadmium and copper. Electrons travel through a wire from the cadmium anode to the copper cathode, causing the cadmium electrode to shrink and the copper electrode to grow. As the electrons travel, a voltmeter measures the electromotive force in volts that the reaction releases. Finally, a salt bridge (with a neutral salt) connects the two half-cells to maintain neutrality.
We can take a closer look at a similar example of a galvanic cell with a zinc and copper reaction below:
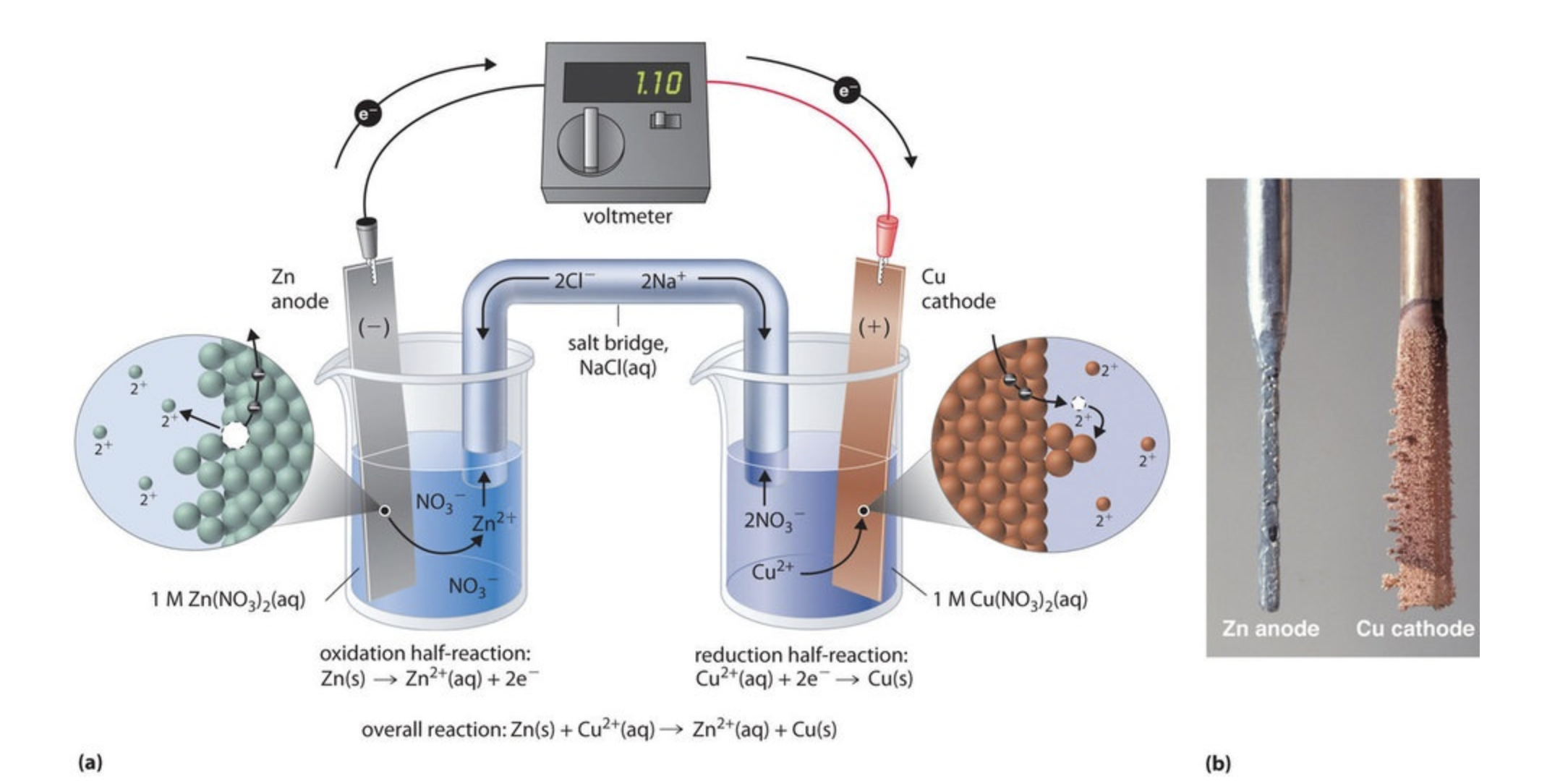
Image From LibreTexts
For this cell, the copper electrode will grow, and the zinc electrode will shrink, which is typical of an anode and cathode in galvanic cells.
On the right, we have an electrolytic cell. The first notable difference is the direction that the electrons travel. In the galvanic cell, electrons traveled from the cadmium to the copper electrode (and eventually to the Cu2+ to create Cu metal). The electrolytic cell has the opposite occurring. Copper metal oxidizes into Cu2+, and Cd2+ reduces into Cd metal, the inverse reaction of the one in the galvanic cell.
Instead of a voltmeter to measure voltage, a power supply (similar to a battery) is used to produce an electromotive force of at least 0.74 V. Because the reaction occurring in the electrolytic cell is nonspontaneous, it requires an external source of energy of this magnitude to run. The reaction also includes a salt bridge because it is two separate half-cells. In this example, the copper electrode will shrink, and the cadmium electrode will grow.
A major similarity between the two types of cells is that always, always, ALWAYS, oxidation occurs at the anode, and reduction occurs at the cathode. No matter what type the cell is (galvanic or electrolytic), this is the standard method used to label electrodes.
The following comparison emphasizes additional differences between the cell types:
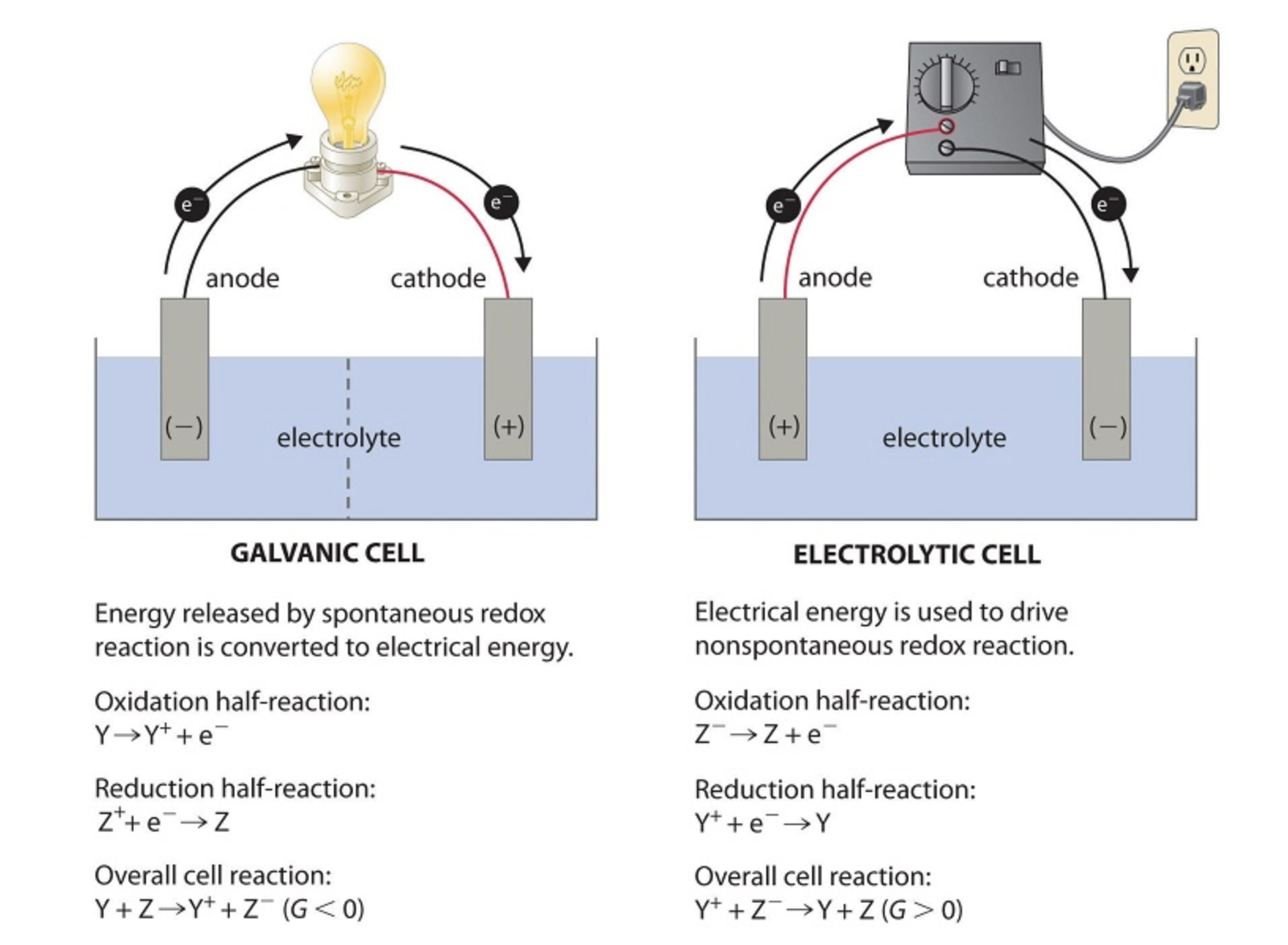
Image From LibreTexts
Faraday’s Law and Electrolysis Problems ⚡
An essential type of problem regarding electrolytic cells is calculating the mass of a metal that accumulates at an electrode. To do this, we want to complete a chain of conversions using the definition of an amp (1A = 1C/s) and Faraday’s constant (1 mol e- = 96485 coulombs), represented as I = q / t, where I is the current in amps, q is charge in coulombs, and t is time in seconds. Ultimately, using Faraday's law, we can calculate the amount of charge flow based on changes in the amounts of reactants and products in an electrochemical cell.
Take a look at this example problem:
Determine the mass of chromium that can be produced when a solution of Cr(NO3)2 is electrolyzed for 60 minutes with a current of 15 amps.
To begin with, we need to convert from amps to coulombs:
60 minutes * 60s/min * 15 C/s = 54000 coulombs
Next, we can use this value of charge to convert to moles of electrons:
54000 coulombs * 1 mol e-/96485C = 0.559 mol e-
Then, we can use stoichiometry to convert from mol e- to moles of chromium. After that, we use the molar mass of chromium (52.0 g/mol) to convert to grams:
0.559 mol e- * (1 mol Cr/2 mol e-) * (52g/mol Cr) = 14.55g Cr produced.
This sort of dimensional analysis can also be done in one long chain as follows:
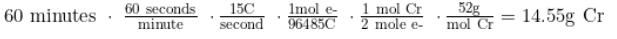
Prepare to solve for any of these unknowns: the number of electrons transferred, the mass of material deposited on or removed from an electrode, current, time elapsed, or the charge of ionic species. A problem could ask about finding the time necessary to produce a certain mass or the amperage required for a given time to produce a mass. To complete problems like these, you can simply manipulate the chain we completed previously.
For example, if a problem asked for a time but gave a mass, you could start with the mass, convert it to moles, then convert it to moles of electrons, then convert it to charge, and then to amperage.
We just need to do proper unit cancellation. Look at the units here:

Now you know how to use Faraday's constant to solve electrolysis problems!
<< Hide Menu
Jillian Holbrook
Jillian Holbrook
You made it to the last topic section of AP Chemistry. Before jumping in, congratulate yourself for making it this far! Over the AP Chem course, you have learned everything from acids and bases to equilibrium to thermodynamics.
For our final topic of Unit 9 and AP Chemistry, we will discuss nonspontaneous redox reactions and how we can use electrolytic cells to make them happen. This builds on the foundations of how electrolytic cells work, how we can differentiate galvanic (or voltaic) cells from electrolytic cells, and how to use Faraday's Law to make electrolysis calculations.
Review of Electrolytic Cells 🔋
As we learned in the introduction of galvanic and electrolytic cells, an electrolytic cell is a cell in which power from an external source (usually a battery) is used to spur nonspontaneous redox reactions by creating electromotive force. Electrolytic cells require energy because they are thermodynamically unfavorable, and therefore nonspontaneous. This means that a chemical species in an electrolytic reaction that would normally be oxidized is instead reduced and vice versa.
Take a look at an example of an electrolytic cell with Zinc and Copper:

Image From Abigail Giordano
In this image, we see that electrons are being pumped out of Cu to form Cu2+ and transferred to Zn2+ to form Zinc metal. The arrows show the direction of the electron flow, meaning the redox reaction occurring is: Cu + Zn2+ → Cu2+ + Zn.
By using a table of standard reduction potentials, we can calculate the cell potential, Ecell:
First, we write out our half-reactions:
Cu → Cu2+ + 2e- (E = -0.34 V)
Zn2+ + 2e- → Zn (E = -0.76 V)
Adding our E values, we find that Ecell = -1.10 V. Therefore, because of the negative voltage, we must introduce external power to cause the redox reaction to run.
Note on the battery in the cell diagram it must be a battery with a voltage of over 1.10 V. This is because the voltage must be enough to overcome the non-spontaneity of the redox reaction we want to occur (and also the spontaneousness of the reverse reaction which has an E value of +1.10 V). When we connect this battery, the voltage pulls electrons in the direction of the nonspontaneous reaction. Therefore, the mass of the copper electrode will decrease, and the mass of the zinc electrode will increase.
Comparing Electrolytic and Galvanic Cells
There are some important differences between a galvanic cell and an electrolytic cell that are necessary to know and recognize for the AP exam. Examine the following galvanic cell and electrolytic cell side by side:

Image From LibreTexts
On the left, the galvanic cell has an anode where oxidation occurs and a cathode where reduction occurs. The reaction occurring is with cadmium and copper. Electrons travel through a wire from the cadmium anode to the copper cathode, causing the cadmium electrode to shrink and the copper electrode to grow. As the electrons travel, a voltmeter measures the electromotive force in volts that the reaction releases. Finally, a salt bridge (with a neutral salt) connects the two half-cells to maintain neutrality.
We can take a closer look at a similar example of a galvanic cell with a zinc and copper reaction below:

Image From LibreTexts
For this cell, the copper electrode will grow, and the zinc electrode will shrink, which is typical of an anode and cathode in galvanic cells.
On the right, we have an electrolytic cell. The first notable difference is the direction that the electrons travel. In the galvanic cell, electrons traveled from the cadmium to the copper electrode (and eventually to the Cu2+ to create Cu metal). The electrolytic cell has the opposite occurring. Copper metal oxidizes into Cu2+, and Cd2+ reduces into Cd metal, the inverse reaction of the one in the galvanic cell.
Instead of a voltmeter to measure voltage, a power supply (similar to a battery) is used to produce an electromotive force of at least 0.74 V. Because the reaction occurring in the electrolytic cell is nonspontaneous, it requires an external source of energy of this magnitude to run. The reaction also includes a salt bridge because it is two separate half-cells. In this example, the copper electrode will shrink, and the cadmium electrode will grow.
A major similarity between the two types of cells is that always, always, ALWAYS, oxidation occurs at the anode, and reduction occurs at the cathode. No matter what type the cell is (galvanic or electrolytic), this is the standard method used to label electrodes.
The following comparison emphasizes additional differences between the cell types:

Image From LibreTexts
Faraday’s Law and Electrolysis Problems ⚡
An essential type of problem regarding electrolytic cells is calculating the mass of a metal that accumulates at an electrode. To do this, we want to complete a chain of conversions using the definition of an amp (1A = 1C/s) and Faraday’s constant (1 mol e- = 96485 coulombs), represented as I = q / t, where I is the current in amps, q is charge in coulombs, and t is time in seconds. Ultimately, using Faraday's law, we can calculate the amount of charge flow based on changes in the amounts of reactants and products in an electrochemical cell.
Take a look at this example problem:
Determine the mass of chromium that can be produced when a solution of Cr(NO3)2 is electrolyzed for 60 minutes with a current of 15 amps.
To begin with, we need to convert from amps to coulombs:
60 minutes * 60s/min * 15 C/s = 54000 coulombs
Next, we can use this value of charge to convert to moles of electrons:
54000 coulombs * 1 mol e-/96485C = 0.559 mol e-
Then, we can use stoichiometry to convert from mol e- to moles of chromium. After that, we use the molar mass of chromium (52.0 g/mol) to convert to grams:
0.559 mol e- * (1 mol Cr/2 mol e-) * (52g/mol Cr) = 14.55g Cr produced.
This sort of dimensional analysis can also be done in one long chain as follows:
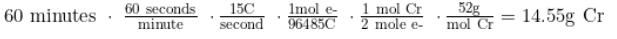
Prepare to solve for any of these unknowns: the number of electrons transferred, the mass of material deposited on or removed from an electrode, current, time elapsed, or the charge of ionic species. A problem could ask about finding the time necessary to produce a certain mass or the amperage required for a given time to produce a mass. To complete problems like these, you can simply manipulate the chain we completed previously.
For example, if a problem asked for a time but gave a mass, you could start with the mass, convert it to moles, then convert it to moles of electrons, then convert it to charge, and then to amperage.
We just need to do proper unit cancellation. Look at the units here:

Now you know how to use Faraday's constant to solve electrolysis problems!

© 2025 Fiveable Inc. All rights reserved.