Browse By Unit
9.7 Galvanic (Voltaic) and Electrolytic Cells
6 min read•june 18, 2024
Jillian Holbrook
Jillian Holbrook
Electrochemistry ⚡
Throughout this unit, we centered most of our discussion around the topics of entropy and Gibbs Free Energy. However, another aspect of energy we have yet to discuss is electricity!
Electrochemistry is the study of redox reactions and how we can use redox reactions to produce electrical energy. To understand electrochemistry and its applications, we will examine cell potentials, which are a measure of the voltage released during redox reactions. Then, we can connect that voltage to spontaneity and equilibrium. We will also look at how electrical power can make nonspontaneous redox reactions occur.
Review of Redox Reactions
Before jumping into the thermodynamics of electrochemistry, we need to review redox reactions from Unit 4. A redox reaction, also known as an oxidation-reduction reaction, is a reaction in which electrons transfer from a reducing agent to an oxidizing agent.
The reducing agent is oxidized (loses electrons), and the oxidizing agent is reduced (gains electrons). A good acronym to remember this concept is OIL RIG (oxidation is loss; reduction is gain). The language of reducing and oxidizing agents is not specifically referenced on the exam, but it is helpful to know in developing a conceptual understanding of the chemistry occurring.
An example of a redox reaction is 2AgNO3 + Cu → Cu(NO3)2 + 2Ag. We see that copper begins at an oxidation number of 0 and ends with an oxidation number of +2. Silver starts with an oxidation number of +1 and ends with an oxidation number of 0. Therefore, copper was oxidized, and silver was reduced. Electrons were transferred from copper to silver.

We can write the above reaction in terms of an oxidation and reduction half-reaction that add together to form the overall reaction:
Copper is oxidized to form Cu2+: Cu → Cu2+ + 2e-
Ag+ is reduced to form Ag: 2Ag+ + 2e- → 2Ag
(Note that we multiplied the second reaction by 2 to balance the electrons!)
Reduction Potentials
When redox reactions occur, the electrons experience an electromotive force, a force pushing electrons from a reducing agent to an oxidizing agent. The stronger the electromotive force, the more spontaneous the reaction. Electromotive force measurements are in volts. We will be using these measurements to calculate cell potential.
We can look at an example of how to calculate the voltage of a redox reaction by using standard reduction potentials. Standard reduction potentials are the voltage of a reduction. Note that voltages can be negative, meaning it takes energy to make the reaction happen. Reduction potentials are a set of calculated constants provided to you. The table of standard reduction potential values we will be referencing is here.
Consider the redox reaction: Zn(s) + Pb2+(aq) → Zn2+(aq) + Pb(s).
First, we can split the reaction into two half-reactions:
Zn → Zn2+ + 2e- (oxidation)
Pb2+ + 2e- → Pb (reduction)
Looking at our chart, we see that the reduction potential for Pb2+ is -0.13 V, and for Zn2+, the reduction potential is -0.76 V. However, our half-reaction for Zn2+ is an oxidation reaction. Flipping a reduction potential reaction negates the potential, meaning the potential for Zn → Zn2+ + 2e- is +0.76 V. Finally, we can add these two numbers together to find that the potential for the overall reaction is -0.13 + 0.76 = 0.63 V.
NOTE: Multiplying a half-reaction does not change the potential!
To find the E value for any given redox reaction, you can use the equation E = Ered - Eox, meaning we could have also done: (-0.13 V) - (-0.76 V) = +0.63 V in our previous example. Later in this unit, we will look at calculating cellular energy, Ecell, using cathodes and anodes of galvanic cells.
Galvanic/Voltaic Cells
Now that we refreshed redox reactions and learned a bit about reduction potentials, we can better understand what happens when the oxidizing agent and reducing agent are separated and connected through a wire. Remember that the oxidizing agent gains electrons and the reducing agent loses electrons. Therefore, electrons will travel through the wire from the reducing agent to the oxidizing agent. The force at which these electrons travel is the cell potential notated as Ecell.
The part of the cell where oxidation occurs is known as the anode, and reduction occurs at the cathode. Electrons travel from the anode to the cathode. A good way of remembering this is the phrase “An Ox, Red Cat,” which tells you that the anode is where oxidation occurs, and the cathode is where reduction occurs.
These cells are known as galvanic or voltaic cells. Take the reaction Cu + 2Ag+ → 2Ag + Cu2+:
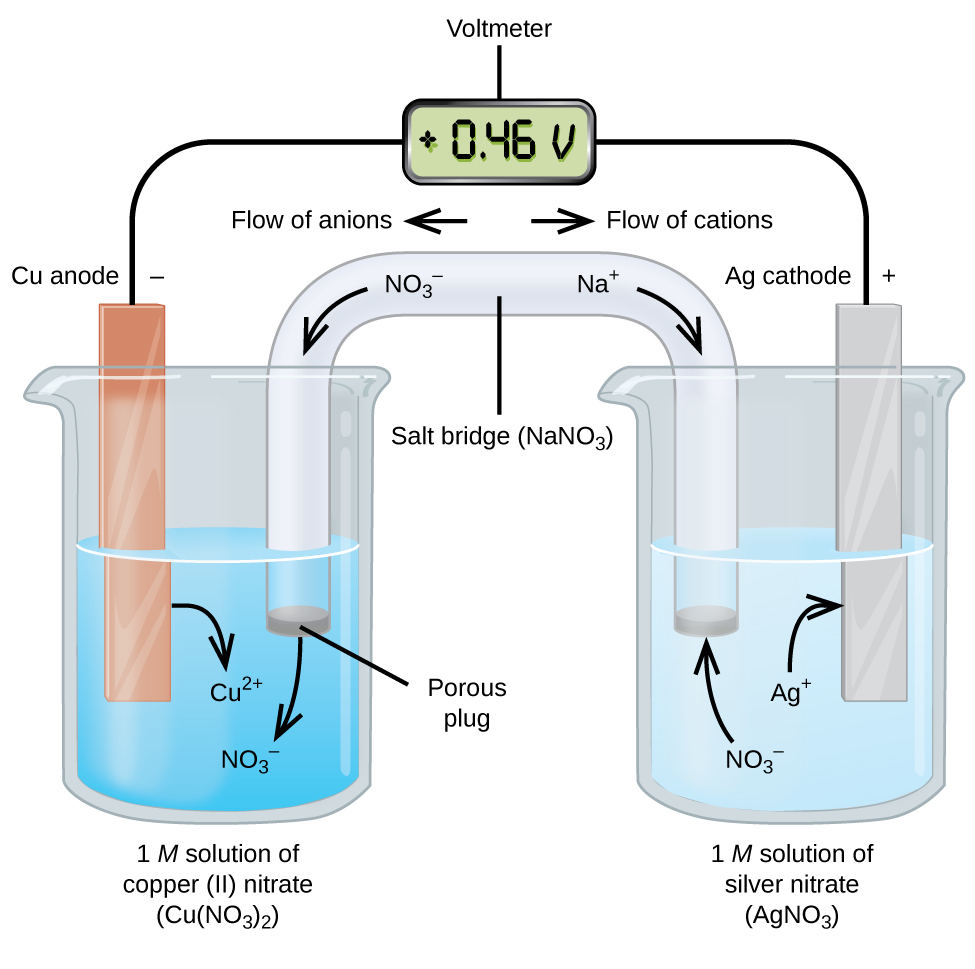
Image From BCCampus
In this image, we see two half-reactions occurring. One of these is the reduction of Ag+ into silver metal, and the other is the oxidation of Cu into Cu2+. Therefore, we have a copper anode and a silver cathode.
When a wire connects these two electrodes in solutions of their respective ions (Cu2+ and Ag+), electrons can travel from the copper to the Ag+ and create Ag. As a result of this chemical process, we see the copper anode shrink and the silver cathode grow because we are losing Cu and forming Cu2+ and losing Ag+ to form Ag. We can add a voltmeter to the wire to measure the electromotive force of this reaction, which we find to be +0.46 V.
The two solutions connect via a salt bridge, which ensures continuous ion flow. A salt bridge is typically a highly soluble salt whose purpose is to act as a source of spectator ions that can migrate into each half-cell to preserve neutrality. They are full of inert ions that will not interact with the reaction. In the example case, we used NaNO3.
As a practice exercise, see if you can write out the half-reactions and find the cell potential using the equation we looked at earlier. You should get the same number (Ecell = 0.46 V). As another exercise, try to logically understand why we can write Ecell = Ecathode - Eanode using E = Ered - Eox.
Electrolytic Cells 🔋
For a galvanic cell, we assume that the Ecell is greater than 0, which means that the reaction occurs spontaneously. However, if we want to drive a nonspontaneous redox reaction, we use voltage to make it happen. Cells where we drive nonspontaneous redox reactions, and Ecell is less than 0, are electrolytic cells.
Suppose we want to rip apart a solution of Na+ and Cl- ions to form the original Na and Cl2 that created the solution: 2NaCl → 2Na + Cl2. This is a nonspontaneous redox reaction, so we can use a battery to create an electromotive force to pull the electron off Cl- and add it to Na+.
First, we can mathematically demonstrate that this reaction is nonspontaneous. Using half-reactions, we can calculate Ecell for this redox reaction:
2Na+ + 2e- → 2Na (E = -2.71 V)
2Cl- → Cl2 + 2e- (E = -1.36 V)
The anode is where oxidation occurs, so Eanode = -1.36 V. The cathode is where reduction occurs, so Ecathode = -2.71 V. We know that Ecell = Ecathode - Eanode = -2.71 V - (-1.36 V) = -1.35 V. Because Ecell for this redox reaction is negative, it will not occur spontaneously. Therefore, we have to use a battery (or some other source of electricity) to actively push electrons from the anode to the cathode.

Image From TropicSU
Because we have molten NaCl (the ions themselves), we use inert electrodes to collect the products, which in this case are Cl2 gas and Na metal. As the electrons are propelled by the voltage of the battery, the Cl- in solution is oxidized into Cl2, and Na+ ions are reduced into Na, meaning gas bubbles will accumulate on the anode and sodium metal will develop on the cathode. Note that the voltage of the battery must be greater than or equal to the voltage of the overall redox reaction. In this example, we must use, at a minimum, a 1.35 V battery.
Learning Summary
We learned that electrochemistry with redox reactions is applicable to measure cell potential in terms of voltage. Oxidation, the gain of electrons, occurs at the anode of an electrochemical cells. Reduction, the loss of electrons, takes place at the cathode.
Galvanic or voltaic cells have spontaneous, thermodynamically favored reactions. Conversely, electrolytic cells involve nonspontaneous, thermodynamically unfavored reactions. Electrolytic cells, due to their thermodynamically unfavorable reactions, require a battery (or other energy source) to produce electromotive force for electron transfer.
Through writing half-reactions and interpreting visual representations of cells, we can analyze how half-reactions occur and in what direction current flows. In combination, these learning objectives support an overall understanding of electrochemistry!
<< Hide Menu
9.7 Galvanic (Voltaic) and Electrolytic Cells
6 min read•june 18, 2024
Jillian Holbrook
Jillian Holbrook
Electrochemistry ⚡
Throughout this unit, we centered most of our discussion around the topics of entropy and Gibbs Free Energy. However, another aspect of energy we have yet to discuss is electricity!
Electrochemistry is the study of redox reactions and how we can use redox reactions to produce electrical energy. To understand electrochemistry and its applications, we will examine cell potentials, which are a measure of the voltage released during redox reactions. Then, we can connect that voltage to spontaneity and equilibrium. We will also look at how electrical power can make nonspontaneous redox reactions occur.
Review of Redox Reactions
Before jumping into the thermodynamics of electrochemistry, we need to review redox reactions from Unit 4. A redox reaction, also known as an oxidation-reduction reaction, is a reaction in which electrons transfer from a reducing agent to an oxidizing agent.
The reducing agent is oxidized (loses electrons), and the oxidizing agent is reduced (gains electrons). A good acronym to remember this concept is OIL RIG (oxidation is loss; reduction is gain). The language of reducing and oxidizing agents is not specifically referenced on the exam, but it is helpful to know in developing a conceptual understanding of the chemistry occurring.
An example of a redox reaction is 2AgNO3 + Cu → Cu(NO3)2 + 2Ag. We see that copper begins at an oxidation number of 0 and ends with an oxidation number of +2. Silver starts with an oxidation number of +1 and ends with an oxidation number of 0. Therefore, copper was oxidized, and silver was reduced. Electrons were transferred from copper to silver.

We can write the above reaction in terms of an oxidation and reduction half-reaction that add together to form the overall reaction:
Copper is oxidized to form Cu2+: Cu → Cu2+ + 2e-
Ag+ is reduced to form Ag: 2Ag+ + 2e- → 2Ag
(Note that we multiplied the second reaction by 2 to balance the electrons!)
Reduction Potentials
When redox reactions occur, the electrons experience an electromotive force, a force pushing electrons from a reducing agent to an oxidizing agent. The stronger the electromotive force, the more spontaneous the reaction. Electromotive force measurements are in volts. We will be using these measurements to calculate cell potential.
We can look at an example of how to calculate the voltage of a redox reaction by using standard reduction potentials. Standard reduction potentials are the voltage of a reduction. Note that voltages can be negative, meaning it takes energy to make the reaction happen. Reduction potentials are a set of calculated constants provided to you. The table of standard reduction potential values we will be referencing is here.
Consider the redox reaction: Zn(s) + Pb2+(aq) → Zn2+(aq) + Pb(s).
First, we can split the reaction into two half-reactions:
Zn → Zn2+ + 2e- (oxidation)
Pb2+ + 2e- → Pb (reduction)
Looking at our chart, we see that the reduction potential for Pb2+ is -0.13 V, and for Zn2+, the reduction potential is -0.76 V. However, our half-reaction for Zn2+ is an oxidation reaction. Flipping a reduction potential reaction negates the potential, meaning the potential for Zn → Zn2+ + 2e- is +0.76 V. Finally, we can add these two numbers together to find that the potential for the overall reaction is -0.13 + 0.76 = 0.63 V.
NOTE: Multiplying a half-reaction does not change the potential!
To find the E value for any given redox reaction, you can use the equation E = Ered - Eox, meaning we could have also done: (-0.13 V) - (-0.76 V) = +0.63 V in our previous example. Later in this unit, we will look at calculating cellular energy, Ecell, using cathodes and anodes of galvanic cells.
Galvanic/Voltaic Cells
Now that we refreshed redox reactions and learned a bit about reduction potentials, we can better understand what happens when the oxidizing agent and reducing agent are separated and connected through a wire. Remember that the oxidizing agent gains electrons and the reducing agent loses electrons. Therefore, electrons will travel through the wire from the reducing agent to the oxidizing agent. The force at which these electrons travel is the cell potential notated as Ecell.
The part of the cell where oxidation occurs is known as the anode, and reduction occurs at the cathode. Electrons travel from the anode to the cathode. A good way of remembering this is the phrase “An Ox, Red Cat,” which tells you that the anode is where oxidation occurs, and the cathode is where reduction occurs.
These cells are known as galvanic or voltaic cells. Take the reaction Cu + 2Ag+ → 2Ag + Cu2+:

Image From BCCampus
In this image, we see two half-reactions occurring. One of these is the reduction of Ag+ into silver metal, and the other is the oxidation of Cu into Cu2+. Therefore, we have a copper anode and a silver cathode.
When a wire connects these two electrodes in solutions of their respective ions (Cu2+ and Ag+), electrons can travel from the copper to the Ag+ and create Ag. As a result of this chemical process, we see the copper anode shrink and the silver cathode grow because we are losing Cu and forming Cu2+ and losing Ag+ to form Ag. We can add a voltmeter to the wire to measure the electromotive force of this reaction, which we find to be +0.46 V.
The two solutions connect via a salt bridge, which ensures continuous ion flow. A salt bridge is typically a highly soluble salt whose purpose is to act as a source of spectator ions that can migrate into each half-cell to preserve neutrality. They are full of inert ions that will not interact with the reaction. In the example case, we used NaNO3.
As a practice exercise, see if you can write out the half-reactions and find the cell potential using the equation we looked at earlier. You should get the same number (Ecell = 0.46 V). As another exercise, try to logically understand why we can write Ecell = Ecathode - Eanode using E = Ered - Eox.
Electrolytic Cells 🔋
For a galvanic cell, we assume that the Ecell is greater than 0, which means that the reaction occurs spontaneously. However, if we want to drive a nonspontaneous redox reaction, we use voltage to make it happen. Cells where we drive nonspontaneous redox reactions, and Ecell is less than 0, are electrolytic cells.
Suppose we want to rip apart a solution of Na+ and Cl- ions to form the original Na and Cl2 that created the solution: 2NaCl → 2Na + Cl2. This is a nonspontaneous redox reaction, so we can use a battery to create an electromotive force to pull the electron off Cl- and add it to Na+.
First, we can mathematically demonstrate that this reaction is nonspontaneous. Using half-reactions, we can calculate Ecell for this redox reaction:
2Na+ + 2e- → 2Na (E = -2.71 V)
2Cl- → Cl2 + 2e- (E = -1.36 V)
The anode is where oxidation occurs, so Eanode = -1.36 V. The cathode is where reduction occurs, so Ecathode = -2.71 V. We know that Ecell = Ecathode - Eanode = -2.71 V - (-1.36 V) = -1.35 V. Because Ecell for this redox reaction is negative, it will not occur spontaneously. Therefore, we have to use a battery (or some other source of electricity) to actively push electrons from the anode to the cathode.

Image From TropicSU
Because we have molten NaCl (the ions themselves), we use inert electrodes to collect the products, which in this case are Cl2 gas and Na metal. As the electrons are propelled by the voltage of the battery, the Cl- in solution is oxidized into Cl2, and Na+ ions are reduced into Na, meaning gas bubbles will accumulate on the anode and sodium metal will develop on the cathode. Note that the voltage of the battery must be greater than or equal to the voltage of the overall redox reaction. In this example, we must use, at a minimum, a 1.35 V battery.
Learning Summary
We learned that electrochemistry with redox reactions is applicable to measure cell potential in terms of voltage. Oxidation, the gain of electrons, occurs at the anode of an electrochemical cells. Reduction, the loss of electrons, takes place at the cathode.
Galvanic or voltaic cells have spontaneous, thermodynamically favored reactions. Conversely, electrolytic cells involve nonspontaneous, thermodynamically unfavored reactions. Electrolytic cells, due to their thermodynamically unfavorable reactions, require a battery (or other energy source) to produce electromotive force for electron transfer.
Through writing half-reactions and interpreting visual representations of cells, we can analyze how half-reactions occur and in what direction current flows. In combination, these learning objectives support an overall understanding of electrochemistry!

© 2025 Fiveable Inc. All rights reserved.