Browse By Unit
1.6 Conservation of Energy in Fluid Flow
5 min read•june 18, 2024
Krish Gupta
Daniella Garcia-Loos
Krish Gupta
Daniella Garcia-Loos
Conservation of Energy in Fluid Flow
You have most likely already learned about the conservation of energy in a previous course or worked with the ideas of kinetic energy and potential energy. The same principles apply to fluids, with a few small differences. The main difference is that the fluids we work with have densities and volumes, while with solids you mostly deal with masses.
Using the conservation of energy principle and making substitutions using the fact that density = mass/volume we arrive at a formula called Bernoulli’s equation.
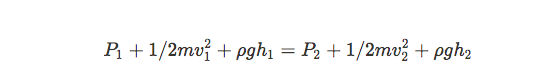
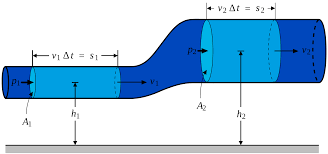
Bernoulli’s equation makes some basic assumptions. If the fluid is incompressible, has streamline (smooth) flow or negligent turbulent (rough) flow, and has negligible viscosity (internal friction), we can use this equation. The test will most likely not give you a situation where you have to deal with these exceptions. Treat this just as you treated air resistance or edge effects in Physics 1. Even though these topics are not usually tested on the exam, it is beneficial to know that they can have some effect on our results.
Water is flowing at a rate of 2m^3/s through a tube with a diameter of 1m. If the pressure at this point is 80kPa, what is the pressure of the water after the tube narrows to a diameter of 0.5m?
We need Bernoulli's equation to solve this problem:
P1 + 1/2ρv1 + ρgh1 = P2 + 1/2ρv2 + ρgh2
The problem statement doesn't tell us that the height changes, so we can remove the last term on each side of the expression, then arrange to solve for the final pressure:
P2 = P1 + 12ρ(v1−v2)
We know the initial pressure, so we still need to calculate the initial and final velocities. We'll use the continuity equation:
V=vA
Rearrange for velocity:
v=V/A
Where A is the cross-sectional area. We can calculate this for each diameter of the tube:
A1 = πd24 = π (1m) 24 = π4m
A2 = πd24 = π (0.5m) 24 = π16m
Now we can calculate the velocity for each diameter:
v1 = 2m3sπ4m = 8πms
v2 = 2m3sπ16m = 32πms
Now we have all of the values needed for Bernoulli's equation, allowing us to solve:
P2 = (80,000Pa) + 12(1000kgm3) (8π−32π)
P2 = (80,000Pa) + (500)(−24π) = 76.2kPa
A special case of this is a leaking tank.
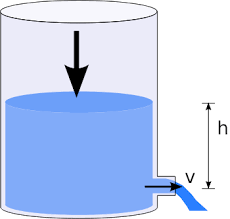
The water at the top of the container has potential and kinetic energy, but so does the water leaking from the side. Since the same amount of water is leaking from the side as is decreasing from the top, their flow rates are equal.
The flow rate is defined as the area multiplied by the velocity of the liquid. More to come on this in the final section.
Since the top has a much bigger area, its velocity is almost negligible and hence we ignore the kinetic energy at the top. Also, since both the top and the leak are exposed to the atmosphere we ignore the initial pressures.
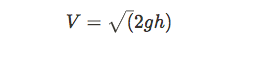
You can see how this equation reminds us of an object in free fall from the kinematics unit from Physics 1. PHYSICS CONNECTS TOGETHER.
Here are some key things to remember about the conservation of energy in fluid flow:
- The conservation of energy is a fundamental principle of physics that states that energy cannot be created or destroyed, only converted from one form to another.
- In fluid flow, the conservation of energy is often used to analyze the transfer of energy from one point to another in a fluid system.
- The energy of a fluid system can be divided into two main categories: kinetic energy and potential energy.
- Kinetic energy is the energy of motion. It is equal to 1/2 * mv^2, where m is the mass of the fluid and v is its velocity.
- Potential energy is the energy of position. It is equal to mgh, where m is the mass of the fluid, g is the acceleration due to gravity, and h is the height of the fluid above a reference point.
- The total energy of a fluid system is equal to the sum of the kinetic and potential energies of the fluid.
- In a fluid flow system, the conservation of energy states that the change in the total energy of the fluid is equal to the energy added to or removed from the system.
Example Problem:
A tank contains water at a depth of 2 meters. A pump is used to pump the water to a height of 10 meters above the tank. The pump has a power output of 5 kW. How much work is done by the pump in lifting the water to the top of the tank?
Solution:
To solve this problem, we will use the conservation of energy principle to calculate the work done by the pump.
First, we need to calculate the change in the potential energy of the water as it is lifted from the bottom of the tank to the top of the tank. The potential energy of the water is equal to its mass times the acceleration due to gravity times its height above a reference point.
The mass of the water can be calculated as the volume of the water times its density:
m = V * ρ
The volume of the water can be calculated as the area of the tank times the depth of the water:
V = A * h
Substituting these expressions into the equation for potential energy, we get:
ΔPE = (A * h * ρ) * g * (h2 - h1)
Where h1 is the initial height of the water (2 meters) and h2 is the final height of the water (10 meters).
Next, we need to calculate the work done by the pump. The work done by the pump is equal to the power output of the pump times the time it takes to lift the water to the top of the tank.
W = P * t
We can use the equation for work to solve for the time it takes to lift the water to the top of the tank:
t = W / P
Substituting the values from the problem into the equation for work, we get:
t = (ΔPE) / P
Substituting the expression for the change in potential energy into the equation for time, we get:
t = [(A * h * ρ) * g * (h2 - h1)] / P
Substituting the values from the problem into this equation, we get:
t = [(A * 2 * ρ) * 9.81 * (10 - 2)] / 5
Solving this equation, we find that it takes approximately 7.84 seconds for the pump to lift the water to the top of the tank.
Therefore, the work done by the pump is equal to 5 kW * 7.84 s = 39.2 kJ.
<< Hide Menu
1.6 Conservation of Energy in Fluid Flow
5 min read•june 18, 2024
Krish Gupta
Daniella Garcia-Loos
Krish Gupta
Daniella Garcia-Loos
Conservation of Energy in Fluid Flow
You have most likely already learned about the conservation of energy in a previous course or worked with the ideas of kinetic energy and potential energy. The same principles apply to fluids, with a few small differences. The main difference is that the fluids we work with have densities and volumes, while with solids you mostly deal with masses.
Using the conservation of energy principle and making substitutions using the fact that density = mass/volume we arrive at a formula called Bernoulli’s equation.
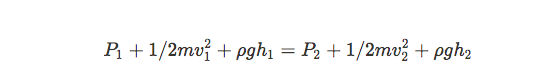

Bernoulli’s equation makes some basic assumptions. If the fluid is incompressible, has streamline (smooth) flow or negligent turbulent (rough) flow, and has negligible viscosity (internal friction), we can use this equation. The test will most likely not give you a situation where you have to deal with these exceptions. Treat this just as you treated air resistance or edge effects in Physics 1. Even though these topics are not usually tested on the exam, it is beneficial to know that they can have some effect on our results.
Water is flowing at a rate of 2m^3/s through a tube with a diameter of 1m. If the pressure at this point is 80kPa, what is the pressure of the water after the tube narrows to a diameter of 0.5m?
We need Bernoulli's equation to solve this problem:
P1 + 1/2ρv1 + ρgh1 = P2 + 1/2ρv2 + ρgh2
The problem statement doesn't tell us that the height changes, so we can remove the last term on each side of the expression, then arrange to solve for the final pressure:
P2 = P1 + 12ρ(v1−v2)
We know the initial pressure, so we still need to calculate the initial and final velocities. We'll use the continuity equation:
V=vA
Rearrange for velocity:
v=V/A
Where A is the cross-sectional area. We can calculate this for each diameter of the tube:
A1 = πd24 = π (1m) 24 = π4m
A2 = πd24 = π (0.5m) 24 = π16m
Now we can calculate the velocity for each diameter:
v1 = 2m3sπ4m = 8πms
v2 = 2m3sπ16m = 32πms
Now we have all of the values needed for Bernoulli's equation, allowing us to solve:
P2 = (80,000Pa) + 12(1000kgm3) (8π−32π)
P2 = (80,000Pa) + (500)(−24π) = 76.2kPa
A special case of this is a leaking tank.

The water at the top of the container has potential and kinetic energy, but so does the water leaking from the side. Since the same amount of water is leaking from the side as is decreasing from the top, their flow rates are equal.
The flow rate is defined as the area multiplied by the velocity of the liquid. More to come on this in the final section.
Since the top has a much bigger area, its velocity is almost negligible and hence we ignore the kinetic energy at the top. Also, since both the top and the leak are exposed to the atmosphere we ignore the initial pressures.
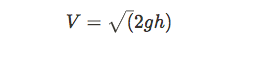
You can see how this equation reminds us of an object in free fall from the kinematics unit from Physics 1. PHYSICS CONNECTS TOGETHER.
Here are some key things to remember about the conservation of energy in fluid flow:
- The conservation of energy is a fundamental principle of physics that states that energy cannot be created or destroyed, only converted from one form to another.
- In fluid flow, the conservation of energy is often used to analyze the transfer of energy from one point to another in a fluid system.
- The energy of a fluid system can be divided into two main categories: kinetic energy and potential energy.
- Kinetic energy is the energy of motion. It is equal to 1/2 * mv^2, where m is the mass of the fluid and v is its velocity.
- Potential energy is the energy of position. It is equal to mgh, where m is the mass of the fluid, g is the acceleration due to gravity, and h is the height of the fluid above a reference point.
- The total energy of a fluid system is equal to the sum of the kinetic and potential energies of the fluid.
- In a fluid flow system, the conservation of energy states that the change in the total energy of the fluid is equal to the energy added to or removed from the system.
Example Problem:
A tank contains water at a depth of 2 meters. A pump is used to pump the water to a height of 10 meters above the tank. The pump has a power output of 5 kW. How much work is done by the pump in lifting the water to the top of the tank?
Solution:
To solve this problem, we will use the conservation of energy principle to calculate the work done by the pump.
First, we need to calculate the change in the potential energy of the water as it is lifted from the bottom of the tank to the top of the tank. The potential energy of the water is equal to its mass times the acceleration due to gravity times its height above a reference point.
The mass of the water can be calculated as the volume of the water times its density:
m = V * ρ
The volume of the water can be calculated as the area of the tank times the depth of the water:
V = A * h
Substituting these expressions into the equation for potential energy, we get:
ΔPE = (A * h * ρ) * g * (h2 - h1)
Where h1 is the initial height of the water (2 meters) and h2 is the final height of the water (10 meters).
Next, we need to calculate the work done by the pump. The work done by the pump is equal to the power output of the pump times the time it takes to lift the water to the top of the tank.
W = P * t
We can use the equation for work to solve for the time it takes to lift the water to the top of the tank:
t = W / P
Substituting the values from the problem into the equation for work, we get:
t = (ΔPE) / P
Substituting the expression for the change in potential energy into the equation for time, we get:
t = [(A * h * ρ) * g * (h2 - h1)] / P
Substituting the values from the problem into this equation, we get:
t = [(A * 2 * ρ) * 9.81 * (10 - 2)] / 5
Solving this equation, we find that it takes approximately 7.84 seconds for the pump to lift the water to the top of the tank.
Therefore, the work done by the pump is equal to 5 kW * 7.84 s = 39.2 kJ.

© 2024 Fiveable Inc. All rights reserved.