Browse By Unit
Krish Gupta
Daniella Garcia-Loos
Krish Gupta
Daniella Garcia-Loos
Resistivity and Resistance
Current Density is a third way of describing the current in terms of the electric field, E, and the material it is traveling through. In this case, we define current density as a vector, J->. We then relate the electric field to the current density through the equation below. (For a full derivation of this equation, check out this link)
ρ is the proportionality constant between E and J and is called the resistivity. Resistivity describes how much a given material restricts the current. Resistivity depends on temperature (higher temperatures result in a higher resistivity, but most tables give values for 20 C)
Current density is a measure of the electric current flowing through a given area, while resistivity is a measure of the resistance of a material to the flow of electric current.
Here are some key points about current density and resistivity:
- Current density is a vector quantity that is defined as the electric current flowing through a given area. It is represented by the symbol "J" and is measured in units of amperes per square meter (A/m^2).
- Current density is related to the electric field in a material. The electric field is the force experienced by a charged particle in the material, and the current density is the flow of charged particles through the material in response to the electric field.
- Resistivity is a measure of the resistance of a material to the flow of electric current. It is represented by the symbol "ρ" (rho) and is measured in units of ohm-meters (Ω-m).
- Resistivity is an intrinsic property of a material and is determined by the type of material and its structure. Materials with high resistivity, such as rubber and glass, are poor conductors of electricity, while materials with low resistivity, such as copper and silver, are good conductors of electricity.
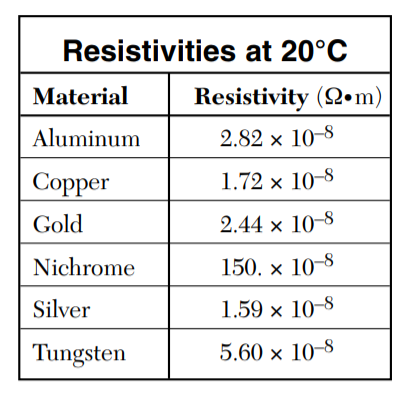
Data from NYS Physics Reference Tables
Resistance 🛑
While resistivity describes how much a material restricts the current, resistance (R) is much more useful for describing a circuit. It takes into account the length (L) and cross-sectional area (A) of the conductor as well.
Resistance is defined as the opposition to current and can be a very useful feature when trying to design a circuit. For example, if the current gets too high in a cell phone, the battery starts expanding and can catch fire or explode.
Resistance is the property of a material or device to oppose the flow of electric current. It is a measure of the difficulty that the material or device presents to the flow of electric charges.
Here are some key points about resistance:
- Resistance is represented by the symbol "R" and is measured in units of ohms (Ω).
- Resistance is an intrinsic property of a material and is determined by the type of material and its structure. Materials with high resistance, such as rubber and glass, are poor conductors of electricity, while materials with low resistance, such as copper and silver, are good conductors of electricity.
- Resistance is also a property of an electrical device or circuit, and it is determined by the characteristics of the device or circuit. For example, a longer wire has a higher resistance than a shorter wire of the same material because the longer wire has more resistance to the flow of electric current.
Resistors in Series & Parallel
Because of Kirchhoff's rules, we can derive handy rules for resistors in series (Rs) and parallel (Rp) circuits.
Looking at these two equations we see an interesting phenomenon. As we add more resistors in series, the total resistance increases. However, adding resistors in parallel reduces the total resistance. An analogy that helps visualize this is relating this to check-out lanes at a grocery store. Even with the world's slowest cashier, opening another lane gets people out quicker than leaving them in a single line.
Ohm's Law 💡
The basic mathematical relationship between resistance and current is defined by Ohm's Law. Depending on your context, it's written one of 3 ways. It doesn't actually matter which one you're more familiar with since they're all the same equation.
This law relates our three main circuit quantities in a nice simple equation. You will often see this represented in graphical form and be asked to infer if the device is Ohmic or non-Ohmic. As you can see in the graph below, an Ohmic device has a constant linear slope, while a non-Ohmic device does not. Sometimes a device can have an Ohmic region, then become non-ohmic.
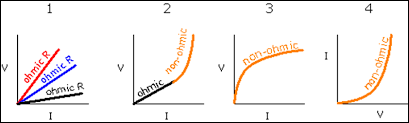
Image from www.menihek.ca/
Ohm's law is a fundamental principle in physics that describes the relationship between electric current, voltage, and resistance in an electrical circuit. It states that the electric current flowing through a conductor is directly proportional to the voltage applied to it and inversely proportional to the resistance of the conductor.
Here are some key points about Ohm's law:
- Ohm's law is represented by the equation I = V/R, where I is the electric current, V is the voltage, and R is the resistance.
- Ohm's law is a fundamental principle in electromagnetism and is used to understand and analyze the flow of electric current in materials and devices.
- Ohm's law is a useful tool for predicting the behavior of electrical circuits and devices and for designing and troubleshooting electrical systems.
- Ohm's law is based on the observation that the electric current flowing through a conductor is directly proportional to the voltage applied to it and inversely proportional to the resistance of the conductor. This means that if the voltage is increased, the current will increase, and if the resistance is increased, the current will decrease.
- Ohm's law is a simplified model of the behavior of electric current and is only strictly valid for conductors that obey Ohm's law. Some materials, such as semiconductors and superconductors, do not obey Ohm's law and have more complex electrical properties.
1.

Answer:
Choice B is correct. Because the resistance of a wire depends on \frac{\rho L}{A}AρL, a longer length and smaller area will result in the greatest resistance
Power in Circuits
Electrical circuits are often used to convert electrical energy into other types of energy. Recall from your previous physics classes that P = work/time. Using this, we can derive an equation for power in electrical terms.
Because of Ohm's Law we can also write this several different ways by subbing in V=IR or I = V/R. Choose the one that best fits the information that's given in the problem.
Practice Question:
1. A hair dryer is rated at 1200W when connected to 120V. What is the resistance of the dryer?
Answer:
Non-Ideal Batteries and EMF 🚨
As often happens with Physics problems, we idealize the 'real-world' problems away when we're doing calculations ("No air resistance", "Frictionless surface", "Ideal gasses", etc). When dealing with circuits, we tend to do this in 2 areas: wires & batteries. With wires, we assume (often correctly) that the resistance of the wires is insignificant to the total resistance of the circuit. However, with batteries, the internal resistance they exhibit is often large enough that we need to take it into account when we apply KVL and other circuit equations.
This leads to us defining a new term: Electromotive Force (EMF) represented by ϵ. EMF is the total energy that can be given to a charge leaving the cell and is related to the terminal voltage by the equation ϵ = VT + Ir, where r is the internal resistance of the battery.

Image from circuitglobe.com
Electromotive force (EMF) is the energy per unit charge that is available to drive electric current through a conductor. It is a measure of the electrical potential difference between two points in an electrical circuit.
Here are some key points about electromotive force:
- Electromotive force is represented by the symbol "E" or "emf" and is measured in units of volts (V).
- Electromotive force is a type of potential difference, or voltage, that can be used to drive electric current through a conductor. It is the energy per unit charge that is available to move the charged particles through the conductor.
- Electromotive force is an important concept in electromagnetism and is used to understand and analyze the operation of electrical devices and circuits.
- Electromotive force is often associated with batteries, generators, and other sources of electric power. It is the energy that is supplied to the circuit by the power source and drives the electric current through the circuit.
- Electromotive force is a scalar quantity, meaning it has only magnitude and no direction. The direction of the electric current is determined by the direction of the flow of the charged particles, which is opposite the direction of the electric field.
<< Hide Menu
Krish Gupta
Daniella Garcia-Loos
Krish Gupta
Daniella Garcia-Loos
Resistivity and Resistance
Current Density is a third way of describing the current in terms of the electric field, E, and the material it is traveling through. In this case, we define current density as a vector, J->. We then relate the electric field to the current density through the equation below. (For a full derivation of this equation, check out this link)
ρ is the proportionality constant between E and J and is called the resistivity. Resistivity describes how much a given material restricts the current. Resistivity depends on temperature (higher temperatures result in a higher resistivity, but most tables give values for 20 C)
Current density is a measure of the electric current flowing through a given area, while resistivity is a measure of the resistance of a material to the flow of electric current.
Here are some key points about current density and resistivity:
- Current density is a vector quantity that is defined as the electric current flowing through a given area. It is represented by the symbol "J" and is measured in units of amperes per square meter (A/m^2).
- Current density is related to the electric field in a material. The electric field is the force experienced by a charged particle in the material, and the current density is the flow of charged particles through the material in response to the electric field.
- Resistivity is a measure of the resistance of a material to the flow of electric current. It is represented by the symbol "ρ" (rho) and is measured in units of ohm-meters (Ω-m).
- Resistivity is an intrinsic property of a material and is determined by the type of material and its structure. Materials with high resistivity, such as rubber and glass, are poor conductors of electricity, while materials with low resistivity, such as copper and silver, are good conductors of electricity.

Data from NYS Physics Reference Tables
Resistance 🛑
While resistivity describes how much a material restricts the current, resistance (R) is much more useful for describing a circuit. It takes into account the length (L) and cross-sectional area (A) of the conductor as well.
Resistance is defined as the opposition to current and can be a very useful feature when trying to design a circuit. For example, if the current gets too high in a cell phone, the battery starts expanding and can catch fire or explode.
Resistance is the property of a material or device to oppose the flow of electric current. It is a measure of the difficulty that the material or device presents to the flow of electric charges.
Here are some key points about resistance:
- Resistance is represented by the symbol "R" and is measured in units of ohms (Ω).
- Resistance is an intrinsic property of a material and is determined by the type of material and its structure. Materials with high resistance, such as rubber and glass, are poor conductors of electricity, while materials with low resistance, such as copper and silver, are good conductors of electricity.
- Resistance is also a property of an electrical device or circuit, and it is determined by the characteristics of the device or circuit. For example, a longer wire has a higher resistance than a shorter wire of the same material because the longer wire has more resistance to the flow of electric current.
Resistors in Series & Parallel
Because of Kirchhoff's rules, we can derive handy rules for resistors in series (Rs) and parallel (Rp) circuits.
Looking at these two equations we see an interesting phenomenon. As we add more resistors in series, the total resistance increases. However, adding resistors in parallel reduces the total resistance. An analogy that helps visualize this is relating this to check-out lanes at a grocery store. Even with the world's slowest cashier, opening another lane gets people out quicker than leaving them in a single line.
Ohm's Law 💡
The basic mathematical relationship between resistance and current is defined by Ohm's Law. Depending on your context, it's written one of 3 ways. It doesn't actually matter which one you're more familiar with since they're all the same equation.
This law relates our three main circuit quantities in a nice simple equation. You will often see this represented in graphical form and be asked to infer if the device is Ohmic or non-Ohmic. As you can see in the graph below, an Ohmic device has a constant linear slope, while a non-Ohmic device does not. Sometimes a device can have an Ohmic region, then become non-ohmic.

Image from www.menihek.ca/
Ohm's law is a fundamental principle in physics that describes the relationship between electric current, voltage, and resistance in an electrical circuit. It states that the electric current flowing through a conductor is directly proportional to the voltage applied to it and inversely proportional to the resistance of the conductor.
Here are some key points about Ohm's law:
- Ohm's law is represented by the equation I = V/R, where I is the electric current, V is the voltage, and R is the resistance.
- Ohm's law is a fundamental principle in electromagnetism and is used to understand and analyze the flow of electric current in materials and devices.
- Ohm's law is a useful tool for predicting the behavior of electrical circuits and devices and for designing and troubleshooting electrical systems.
- Ohm's law is based on the observation that the electric current flowing through a conductor is directly proportional to the voltage applied to it and inversely proportional to the resistance of the conductor. This means that if the voltage is increased, the current will increase, and if the resistance is increased, the current will decrease.
- Ohm's law is a simplified model of the behavior of electric current and is only strictly valid for conductors that obey Ohm's law. Some materials, such as semiconductors and superconductors, do not obey Ohm's law and have more complex electrical properties.
1.

Answer:
Choice B is correct. Because the resistance of a wire depends on \frac{\rho L}{A}AρL, a longer length and smaller area will result in the greatest resistance
Power in Circuits
Electrical circuits are often used to convert electrical energy into other types of energy. Recall from your previous physics classes that P = work/time. Using this, we can derive an equation for power in electrical terms.
Because of Ohm's Law we can also write this several different ways by subbing in V=IR or I = V/R. Choose the one that best fits the information that's given in the problem.
Practice Question:
1. A hair dryer is rated at 1200W when connected to 120V. What is the resistance of the dryer?
Answer:
Non-Ideal Batteries and EMF 🚨
As often happens with Physics problems, we idealize the 'real-world' problems away when we're doing calculations ("No air resistance", "Frictionless surface", "Ideal gasses", etc). When dealing with circuits, we tend to do this in 2 areas: wires & batteries. With wires, we assume (often correctly) that the resistance of the wires is insignificant to the total resistance of the circuit. However, with batteries, the internal resistance they exhibit is often large enough that we need to take it into account when we apply KVL and other circuit equations.
This leads to us defining a new term: Electromotive Force (EMF) represented by ϵ. EMF is the total energy that can be given to a charge leaving the cell and is related to the terminal voltage by the equation ϵ = VT + Ir, where r is the internal resistance of the battery.

Image from circuitglobe.com
Electromotive force (EMF) is the energy per unit charge that is available to drive electric current through a conductor. It is a measure of the electrical potential difference between two points in an electrical circuit.
Here are some key points about electromotive force:
- Electromotive force is represented by the symbol "E" or "emf" and is measured in units of volts (V).
- Electromotive force is a type of potential difference, or voltage, that can be used to drive electric current through a conductor. It is the energy per unit charge that is available to move the charged particles through the conductor.
- Electromotive force is an important concept in electromagnetism and is used to understand and analyze the operation of electrical devices and circuits.
- Electromotive force is often associated with batteries, generators, and other sources of electric power. It is the energy that is supplied to the circuit by the power source and drives the electric current through the circuit.
- Electromotive force is a scalar quantity, meaning it has only magnitude and no direction. The direction of the electric current is determined by the direction of the flow of the charged particles, which is opposite the direction of the electric field.

© 2024 Fiveable Inc. All rights reserved.