Browse By Unit
7.5 Properties of Waves and Particles
5 min read•june 18, 2024
Daniella Garcia-Loos
Saarah Hasan
Daniella Garcia-Loos
Saarah Hasan
From previous lessons, we already know that light behaves as both a particle and a wave. In 7.5, we’re going to expand on this duality.
Wave-Particle Duality
The coexistence of particle and wave properties for fundamental particles is known as wave-particle duality. On a small scale, particles can showcase the properties of waves. Think back to double-slit experiments: if a stream of particles were traveled through the slit, they would diffract. Waves can also showcase properties of particles; photons have particle properties like momentum and energy, which relate to their frequency and wavelength.
In the 1920s, a physicist named Arthur Compton conducted experiments that showed that when an X-ray photon collides with an electron, the collision obeys that law of conservation of momentum. In this momentum interaction, known as the Compton effect, the scattered photon has a lower frequency than the incident photon.
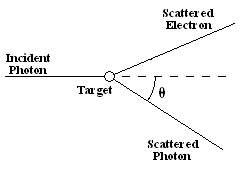
Taken from Wikimedia Commons
The momentum of the photon is given by:
p=h/λ
This raised a question: if an electromagnetic wave, can a particle of matter behave like a wave? A physicist named Louis de Broglie suggested that the answer was yes. Since a photon’s momentum is p=h/λ, the wavelength can be rearranged to
λ=h/p
If the momentum of a particle (p=mv) is big enough to overcome Planck’s constant, a significant wavelength can be observed. For this to happen, the mass has to be extremely small (on the atomic scale). The equation for the de Broglie wavelength of a particle becomes:
λ=h/mv
Wave-particle duality is the concept that particles, such as electrons and photons, can exhibit both wave-like and particle-like behavior. It is a fundamental principle of quantum mechanics that has been confirmed by numerous experiments.
Here are some key points about wave-particle duality:
- Wave-particle duality is the concept that particles, such as electrons and photons, can exhibit both wave-like and particle-like behavior. It is a fundamental principle of quantum mechanics that has been confirmed by numerous experiments.
- Wave-particle duality is a consequence of the wave-particle duality of energy, which states that energy can exhibit both wave-like and particle-like behavior.
- The wave-like behavior of particles is described by wave-like properties such as wavelength, frequency, and amplitude. The particle-like behavior of particles is described by particle-like properties such as mass and charge.
- Wave-particle duality is a key feature of quantum mechanics and is essential for understanding the behavior of particles at the atomic and subatomic level. It has many important implications and applications, including the development of technologies such as lasers and transistors.
- Wave-particle duality is a fundamental principle of quantum mechanics and is an important part of our understanding of the nature of matter and energy. It has had a profound impact on our understanding of the universe and has led to many important discoveries and technological advances.
Let's do some practice together:
Electrons in a diffraction experiment are accelerated through a potential difference of 175 V. What's the de Broglie wavelength of these electrons? p=mv ➡️ p=√(2mK) KE=1/2mv^2 λ=h/p=h/√(2mK) =6.6310^-^3^4 Js/√(2(9.1110^-^3^1 kg))[125 eV1.610^-^1^9 J/1 eV] = 9.310^-^1^1 m = 0.093 nm
Relativistic mass–energy equivalence
Relativistic mass-energy equivalence is the concept that the mass of an object increases as its velocity increases. It is a consequence of the theory of relativity and is described by the equation E=mc^2, where E is energy, m is mass, and c is the speed of light.
Here are some key points about relativistic mass-energy equivalence:
- Relativistic mass-energy equivalence is the concept that the mass of an object increases as its velocity increases. It is a consequence of the theory of relativity and is described by the equation E=mc^2, where E is energy, m is mass, and c is the speed of light.
- The theory of relativity states that the laws of physics are the same for all inertial observers, regardless of their velocity. This means that the mass of an object depends on its velocity, and that the mass of an object increases as its velocity increases.
Wave Phenomena
Interference and diffraction are phenomena that are observed in waves, such as light waves or sound waves. They are not observed in particles, such as electrons or atoms.
Here are some key points about why only waves display interference and diffraction:
- Interference is the phenomenon in which waves combine to form a new wave pattern. It is observed when two or more waves pass through each other.
- Diffraction is the phenomenon in which waves bend around obstacles or pass through small openings. It is observed when waves encounter an obstacle or opening that is comparable in size to the wavelength of the wave.
- Interference and diffraction are phenomena that are observed in waves, such as light waves or sound waves. They are not observed in particles, such as electrons or atoms.
- The reason that only waves display interference and diffraction is that these phenomena are a consequence of the wave nature of the particles. Particles do not have a wave nature, so they do not exhibit these phenomena.
Practice Problems: 🧩
1, An atomic particle of mass m moving at speed v is found to have wavelength λ. What is the wavelength of a second particle with a speed 3v and the same mass? A) (1/9) λ
B) (1/3) λ
C) λ
D) 3 λ
E) 9 λ
2.A very slow proton has its kinetic energy doubled. What happens to the protons corresponding de Broglie wavelength? A) the wavelength is decreased by a factor of √2 B) the wavelength is halved C) there is no change in the wavelength D) the wavelength is increased by a factor of √2 E) the wavelength is doubled.
- Which of the following graphs best represents the de Broglie wavelength λ of a particle as a function of the linear momentum p of the particle?
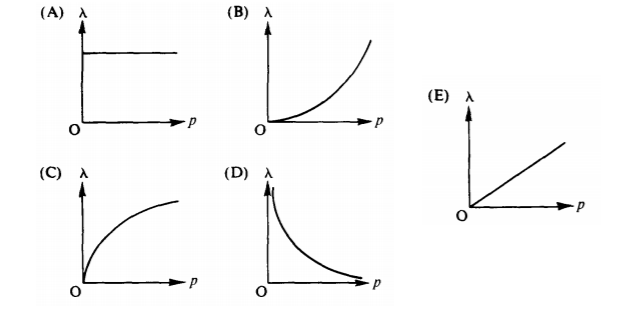
Answers:
- B: de Broglie wavelength is given by, p = h / λ … mv = h / λ … λ = h / mv … 3x m = 1/3 λ
- A: From above λ = h / mv … Since K = ½ mv2 , 2x K means √2x v. So when we plug in the new velocity of √2v, the wavelength decreases by this factor since we divide.
- D: From p=h/ λ, they are inverses.
<< Hide Menu
7.5 Properties of Waves and Particles
5 min read•june 18, 2024
Daniella Garcia-Loos
Saarah Hasan
Daniella Garcia-Loos
Saarah Hasan
From previous lessons, we already know that light behaves as both a particle and a wave. In 7.5, we’re going to expand on this duality.
Wave-Particle Duality
The coexistence of particle and wave properties for fundamental particles is known as wave-particle duality. On a small scale, particles can showcase the properties of waves. Think back to double-slit experiments: if a stream of particles were traveled through the slit, they would diffract. Waves can also showcase properties of particles; photons have particle properties like momentum and energy, which relate to their frequency and wavelength.
In the 1920s, a physicist named Arthur Compton conducted experiments that showed that when an X-ray photon collides with an electron, the collision obeys that law of conservation of momentum. In this momentum interaction, known as the Compton effect, the scattered photon has a lower frequency than the incident photon.

Taken from Wikimedia Commons
The momentum of the photon is given by:
p=h/λ
This raised a question: if an electromagnetic wave, can a particle of matter behave like a wave? A physicist named Louis de Broglie suggested that the answer was yes. Since a photon’s momentum is p=h/λ, the wavelength can be rearranged to
λ=h/p
If the momentum of a particle (p=mv) is big enough to overcome Planck’s constant, a significant wavelength can be observed. For this to happen, the mass has to be extremely small (on the atomic scale). The equation for the de Broglie wavelength of a particle becomes:
λ=h/mv
Wave-particle duality is the concept that particles, such as electrons and photons, can exhibit both wave-like and particle-like behavior. It is a fundamental principle of quantum mechanics that has been confirmed by numerous experiments.
Here are some key points about wave-particle duality:
- Wave-particle duality is the concept that particles, such as electrons and photons, can exhibit both wave-like and particle-like behavior. It is a fundamental principle of quantum mechanics that has been confirmed by numerous experiments.
- Wave-particle duality is a consequence of the wave-particle duality of energy, which states that energy can exhibit both wave-like and particle-like behavior.
- The wave-like behavior of particles is described by wave-like properties such as wavelength, frequency, and amplitude. The particle-like behavior of particles is described by particle-like properties such as mass and charge.
- Wave-particle duality is a key feature of quantum mechanics and is essential for understanding the behavior of particles at the atomic and subatomic level. It has many important implications and applications, including the development of technologies such as lasers and transistors.
- Wave-particle duality is a fundamental principle of quantum mechanics and is an important part of our understanding of the nature of matter and energy. It has had a profound impact on our understanding of the universe and has led to many important discoveries and technological advances.
Let's do some practice together:
Electrons in a diffraction experiment are accelerated through a potential difference of 175 V. What's the de Broglie wavelength of these electrons? p=mv ➡️ p=√(2mK) KE=1/2mv^2 λ=h/p=h/√(2mK) =6.6310^-^3^4 Js/√(2(9.1110^-^3^1 kg))[125 eV1.610^-^1^9 J/1 eV] = 9.310^-^1^1 m = 0.093 nm
Relativistic mass–energy equivalence
Relativistic mass-energy equivalence is the concept that the mass of an object increases as its velocity increases. It is a consequence of the theory of relativity and is described by the equation E=mc^2, where E is energy, m is mass, and c is the speed of light.
Here are some key points about relativistic mass-energy equivalence:
- Relativistic mass-energy equivalence is the concept that the mass of an object increases as its velocity increases. It is a consequence of the theory of relativity and is described by the equation E=mc^2, where E is energy, m is mass, and c is the speed of light.
- The theory of relativity states that the laws of physics are the same for all inertial observers, regardless of their velocity. This means that the mass of an object depends on its velocity, and that the mass of an object increases as its velocity increases.
Wave Phenomena
Interference and diffraction are phenomena that are observed in waves, such as light waves or sound waves. They are not observed in particles, such as electrons or atoms.
Here are some key points about why only waves display interference and diffraction:
- Interference is the phenomenon in which waves combine to form a new wave pattern. It is observed when two or more waves pass through each other.
- Diffraction is the phenomenon in which waves bend around obstacles or pass through small openings. It is observed when waves encounter an obstacle or opening that is comparable in size to the wavelength of the wave.
- Interference and diffraction are phenomena that are observed in waves, such as light waves or sound waves. They are not observed in particles, such as electrons or atoms.
- The reason that only waves display interference and diffraction is that these phenomena are a consequence of the wave nature of the particles. Particles do not have a wave nature, so they do not exhibit these phenomena.
Practice Problems: 🧩
1, An atomic particle of mass m moving at speed v is found to have wavelength λ. What is the wavelength of a second particle with a speed 3v and the same mass? A) (1/9) λ
B) (1/3) λ
C) λ
D) 3 λ
E) 9 λ
2.A very slow proton has its kinetic energy doubled. What happens to the protons corresponding de Broglie wavelength? A) the wavelength is decreased by a factor of √2 B) the wavelength is halved C) there is no change in the wavelength D) the wavelength is increased by a factor of √2 E) the wavelength is doubled.
- Which of the following graphs best represents the de Broglie wavelength λ of a particle as a function of the linear momentum p of the particle?

Answers:
- B: de Broglie wavelength is given by, p = h / λ … mv = h / λ … λ = h / mv … 3x m = 1/3 λ
- A: From above λ = h / mv … Since K = ½ mv2 , 2x K means √2x v. So when we plug in the new velocity of √2v, the wavelength decreases by this factor since we divide.
- D: From p=h/ λ, they are inverses.

© 2024 Fiveable Inc. All rights reserved.