Browse By Unit
7.1 Systems and Fundamental Forces
8 min read•july 22, 2024
Daniella Garcia-Loos
Saarah Hasan
Daniella Garcia-Loos
Saarah Hasan
Unit 7: Quantum, Atomic, and Nuclear Physics
7.1: Systems and Fundamental Forces
Atoms. The smallest and most basic units of matter and the defining structure of elements. In this lesson, we’re going to go over what an atom is made up of, atomic theory, and electron energy levels. After going through this unit you should be able to discuss the internal structure of atoms and their nuclei.
Fundamental Particles
Let’s go over our understanding of what an atom is. Some general information about atoms:
- Atoms are stable and electrically neutral.
- Atoms have chemical properties that allow them to combine with other atoms.
- Atoms emit and absorb electromagnetic radiation with discrete energy and momentum.
- Atoms are made up of three particles: protons, neutrons, and electrons.
| Particle | |||
| Electron | e- | 9.11*10^-31 | -1.6*10^-19 |
| Proton | p | 1.673*10^-27 | 1.6*10^19 |
| Neutron | n | 1.673*10^-27 | No charge! |
Electrons, neutrinos, photons, and quarks are examples of fundamental particles: particles that make up other particles but can’t be broken down (they aren’t composed of other particles). Neutrons and protons are composed of quarks, which have electric charges that are fractions of the elementary charge of the electron.
There are 6 types (flavors) of quarks: up, down, strange, charm, bottom, and top.
- Up, charm, and top have a fractional charge of +⅔
- Down, strange, and bottom have a fractional charge of -⅓

Protons are composed of two ups and one down. Neutrons are composed of two downs and one up. Taken from Wikimedia Commons
The nucleus of the atom is composed of protons and neutrons, which are collectively called nucleons. The number of protons in a nucleus is the atom’s atomic number (Z)—it’s sort of the identifier of an element. Adding the number of neutrons (N) and the number of protons gives the mass number (A) of an element.
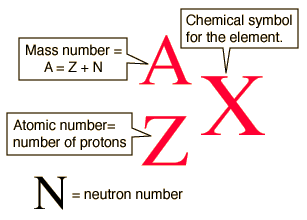
Taken from socratic.org
Nuclei that contain the same numbers of protons but a different number of neutrons are called isotopes.
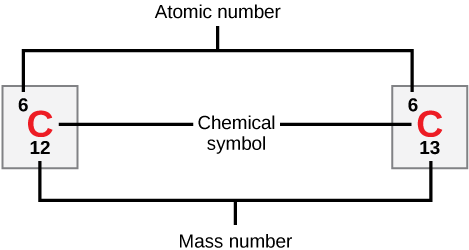
Taken from Wikimedia Commons
Rutherford’s Model
If you’ve taken chemistry, you’re probably familiar with Ernest Rutherford. Rutherford was a physicist who decided to test out J.J. Thompson’s model of an atom, which proposed that an atom consisted of a relatively large, uniformly distributed, positive mass with negatively charged electrons embedded throughout the atom.
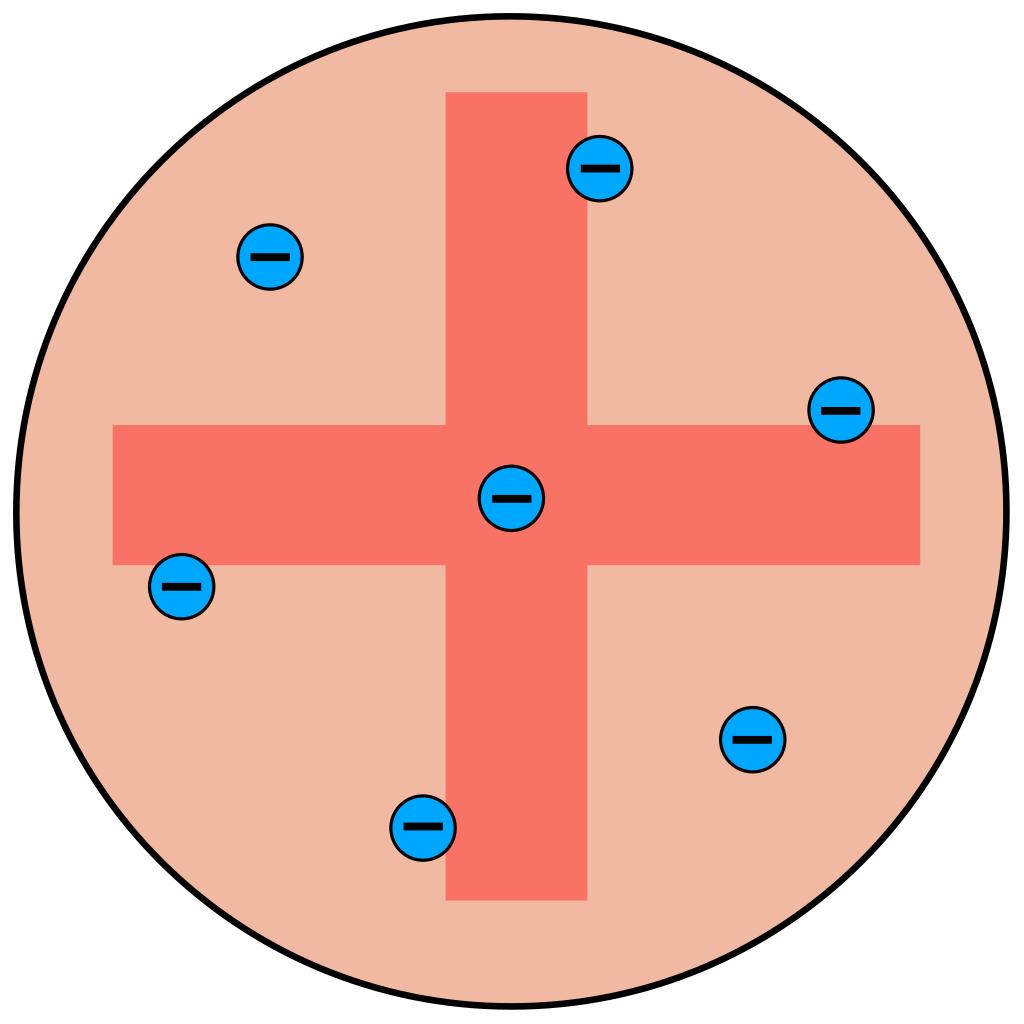
J.J. Thompson "plum pudding" model of an atom Taken from Wikimedia Commons
Rutherford’s experiment consisted of aiming alpha particles at a thin sheet of gold foil and observing the scattering pattern on a zinc sulfide screen. Rutherford found that while most of the alpha particles weren’t deflected, some were strongly deflected in hyperbolic paths, and a few were even scattered back close to 180^o180o.
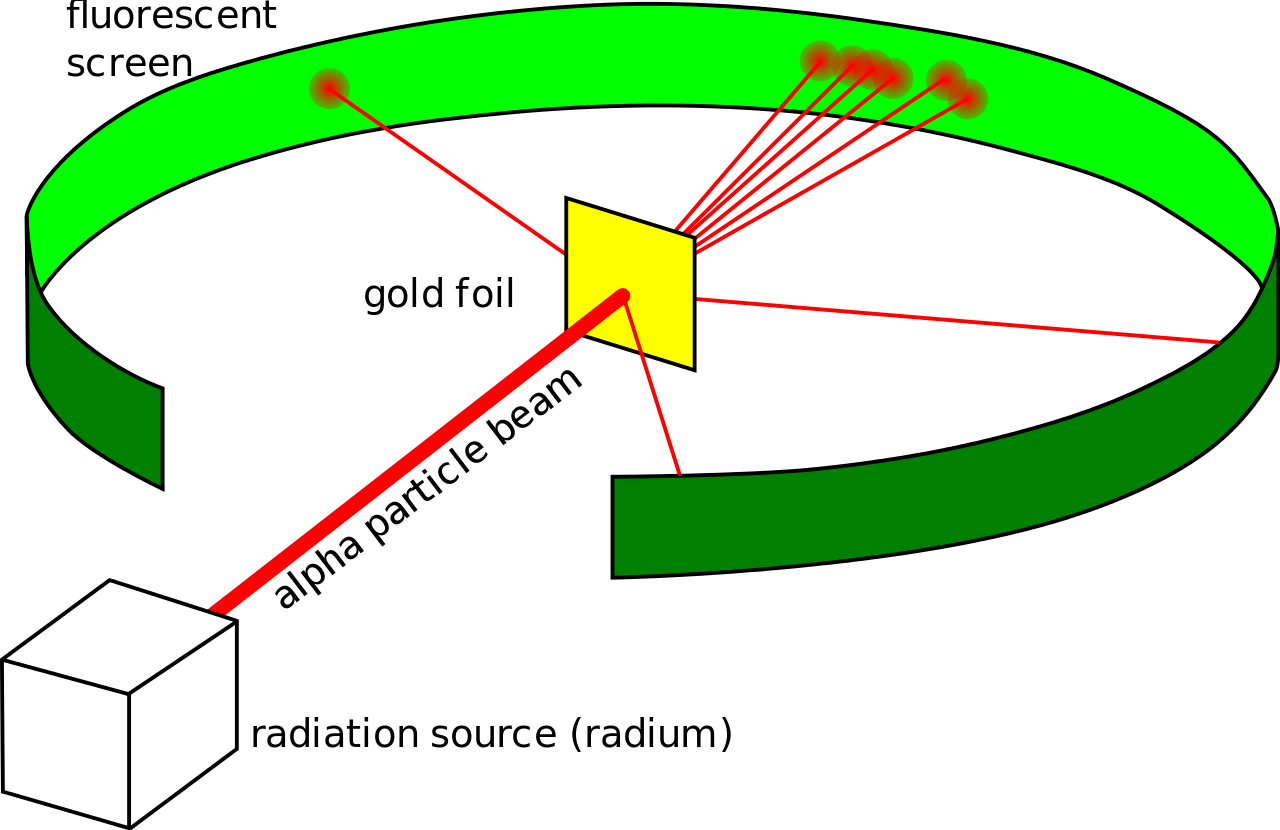
Rutherford's experiment Taken from Wikimedia Commons
Rutherford concluded that the atom consisted of mostly empty space, the nucleus was a very small, densely packed, positive charge, and the electrons orbited around the nucleus like planets orbiting the Sun.
His proposition, however, had several major problems:
- It didn’t account for the appearance of discrete emission line spectra.
- The electrons continuously orbiting the nucleus should've produced a continuous band of electromagnetic radiation, but that doesn’t happen.
- The predicted orbital loss of energy should’ve caused the electron to crash into the nucleus, disintegrating it, but that doesn’t happen,
The Bohr Model
Years after Rutherford’s declaration of his nuclear model of the atom, a physicist named Niels Bohr set out to add an important piece to the atomic puzzle.
Bohr realized that the Balmer formula, which essentially summarizes the visible wavelengths that appear in the emission spectrum of hydrogen, could be looked at in terms of energy differences. The main takeaways:
- Electrons don’t emit electromagnetic radiation while in a given orbit.
- An electron can only have a certain set orbits.
- An atom has definite energy levels analogous to standing waves.

Taken from Wikimedia Commons
Here are some key differences between Bohr and Rutherford's models of the atom:
- Bohr's model:- Proposed that electrons orbit the nucleus in fixed, discrete energy levels- Electrons can only jump between energy levels by absorbing or emitting a specific amount of energy (called a "quantum")- Explained the observed emission spectra of hydrogen atoms
- Rutherford's model:- Proposed that the atom consists of a small, dense nucleus (made of protons and neutrons) surrounded by electrons- Explained the scattering of alpha particles in gold foil experiments- Led to the discovery of the proton and the concept of the atomic nucleus Overall, Bohr's model was able to explain the behavior of atoms at a more macroscopic level, while Rutherford's model provided a more detailed, microscopic view of the structure of the atom. Both models were important contributions to our understanding of the nature of atoms and the way they behave.
Let’s zoom in really quick on the nucleus of an atom. Aren’t the protons experiencing a repulsive Coulomb’s force from each other? What’s holding the nucleus together? Well, the presence of another fundamental force stronger than Coulomb’s force is the reason: the strong nuclear force (yes, it’s really called that). The strong nuclear force binds the neutrons and protons together; it’s the strongest force in nature.
Okay, now back to the Bohr Model of the Atom. Remember how we said that an electron has a certain set orbit? Well, if the electron absorbs a certain amount of energy, it gets excited to a higher orbit with a greater radius. After some time, it returns to a lower orbit, emitting a photon while doing so. Since each allowed orbit (energy level) has a specific radius and energy, the photons in each jump have only specific wavelengths.
When the excited electron drops from energy level n=jn=j to a lower one, n=in=i, the energy of the photon emitted is the difference between the two energy levels:
E*(emitted photon)*=|ΔE|=E_j-E_i
The wavelength of this photon is
λ=c/f=c/(Ephoton/h)=hc/(Ej-Ei)
where
c= speed of light =3.00*10^8
h= Planck's' constant = 6.6310^-^3^4 Js
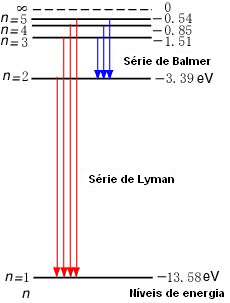
Taken from Wikimedia Commons
Let's look at a practice problem together.
(A) Looking at the energy level diagram for hydrogen above (ignore the Ly equations near the arrows), how much energy must a ground-state electron in a hydrogen atom absorb to be excited to the n=3 energy level?
(B) If an electron jumped to n=4 level, what wavelengths are possible for the photon emitted when the electron drops to a lower energy level? In what regions of the EM spectrum do these photons lie?
(A)
The ground state energy level (n=1) is -13.6 eV and E_3=-1.51 eV.
The energy needed for an electron to jump from E1 to E3:
E_3-E_1=(-1.51 eV)-(-13.6 eV)= 12.09
(B) An electron in the n=4 energy level can drop to n=3, n=2, or all the way down to n=1. The energies of the n=2 and n=3n=3 levels are
E_2=1/2^2(-13.6 eV)=-3.4 eV
E_3=1/3^2(-13.6)=-1.5eV
The 3 possible values for the energy of the emitted photon:
E_4_→_3=E_4-E_3=(-0.85 eV)-(-1.5 eV)=0.65eV
E_4_→_2=E_4-E_2=(-0.85 eV)-(-3.4 eV)=2.55eV
E_4_→_1=E_4-E_1=(-0.85 eV)-(-13.6 eV) 12.8 eV
From the equation E=hf=hc/λ, we get λ=hc/E
λ_4_→_3=(4.1410^-^1^5 eVs)(3.00*10^8 m/s)/(0.65 eV)= 1,910 nm
➡️ In the visible light spectrum; the wavelength matches to the color blue-green
λ_4_→_2=(4.1410^-^1^5 eVs)(3.00*10^8 m/s)/(2.55 eV)=487 nm
➡️ Ultraviolet wavelength
λ_4_→_1=(4.1410^-^1^5 eVs)(3.00*10^8 m/s)/(12.8 eV)=97 nm
➡️Infrared
Practice Problems
- According to the Bohr theory of the hydrogen atom, electrons starting in the 4th energy level and eventually ending up in the ground state, could produce a total of how many lines in the hydrogen spectra?
A) 7
B) 6
C) 5
D) 4
E) 3
- In Rutherford's famous gold foil scattering experiment, he found that most alpha particles would pass through the foil undeflected. Which of the following nuclear properties can be inferred from this observation?
A) The nucleus must have a positive charge
B) Most of the mass of an atom is in the nucleus
C) The nucleus contains both protons and neutrons
D) The diameter of the nucleus is small compared to the diameter of the atom
E) none of the above.
- According to the Bohr model of the atom, electrons orbit the nucleus in definite orbits. According to the laws of classical physics, this model would be impossible because
A) the positively charged nucleus attracts the electrons
B) Coulomb's law applies
C) accelerating electrons radiate energy
D) there is a centripetal force on the electrons
E) angular momentum is conserved

- A hypothetical atom has four energy states as shown.Which of the following photon energies could NOT be found in the emission spectra of this atom after it has been excited to the n = 4 state?
A) 1 eV
B) 2 eV
C) 3 eV
D) 4 eV
E) 5 eV
- Which of the following transitions will produce the photon with the longest wavelength?
A) n = 2 to n = 1
B) n = 3 to n = 1
C) n = 3 to n = 2
D) n = 4 to n = 1
E) n = 4 to n = 3
Answers:
- B: 4–3, 3–2, 2–1 … or 4–2, 2–1 … or 4–3, 3–1 … or 4–1 … this is a total of 6 different transitions.
- D: While Rutherford’s experiment did show most of these, looking at the single fact provided (that most particles pass straight through) only meant that most of the atom was empty space and that the nucleus must be small.
- C: According to classical physics, when charges accelerate in circles, they necessarily radiate energy in the form of light. This would cause them to spiral into the nucleus as they radiate continuous spectrums of color. This does not happen though, which is a flaw in the Rutherford model
- D: Electron jumps could happen as follows 4–3, 3–2, 2–1 … or 4–2, 2–1 … or 4–3, 3–1 … or 4–1.In these emissions from the differences in the energy level graph, we can make all of the energy difference choices except 4 eV.
- E: Big λ means the least energy based on E=hc/ λ. The least energy corresponds to the smallest energy level jump which is 4–3.
<< Hide Menu
7.1 Systems and Fundamental Forces
8 min read•july 22, 2024
Daniella Garcia-Loos
Saarah Hasan
Daniella Garcia-Loos
Saarah Hasan
Unit 7: Quantum, Atomic, and Nuclear Physics
7.1: Systems and Fundamental Forces
Atoms. The smallest and most basic units of matter and the defining structure of elements. In this lesson, we’re going to go over what an atom is made up of, atomic theory, and electron energy levels. After going through this unit you should be able to discuss the internal structure of atoms and their nuclei.
Fundamental Particles
Let’s go over our understanding of what an atom is. Some general information about atoms:
- Atoms are stable and electrically neutral.
- Atoms have chemical properties that allow them to combine with other atoms.
- Atoms emit and absorb electromagnetic radiation with discrete energy and momentum.
- Atoms are made up of three particles: protons, neutrons, and electrons.
| Particle | |||
| Electron | e- | 9.11*10^-31 | -1.6*10^-19 |
| Proton | p | 1.673*10^-27 | 1.6*10^19 |
| Neutron | n | 1.673*10^-27 | No charge! |
Electrons, neutrinos, photons, and quarks are examples of fundamental particles: particles that make up other particles but can’t be broken down (they aren’t composed of other particles). Neutrons and protons are composed of quarks, which have electric charges that are fractions of the elementary charge of the electron.
There are 6 types (flavors) of quarks: up, down, strange, charm, bottom, and top.
- Up, charm, and top have a fractional charge of +⅔
- Down, strange, and bottom have a fractional charge of -⅓

Protons are composed of two ups and one down. Neutrons are composed of two downs and one up. Taken from Wikimedia Commons
The nucleus of the atom is composed of protons and neutrons, which are collectively called nucleons. The number of protons in a nucleus is the atom’s atomic number (Z)—it’s sort of the identifier of an element. Adding the number of neutrons (N) and the number of protons gives the mass number (A) of an element.
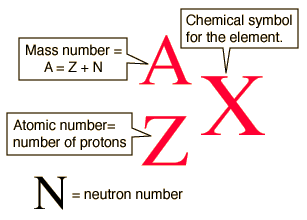
Taken from socratic.org
Nuclei that contain the same numbers of protons but a different number of neutrons are called isotopes.

Taken from Wikimedia Commons
Rutherford’s Model
If you’ve taken chemistry, you’re probably familiar with Ernest Rutherford. Rutherford was a physicist who decided to test out J.J. Thompson’s model of an atom, which proposed that an atom consisted of a relatively large, uniformly distributed, positive mass with negatively charged electrons embedded throughout the atom.

J.J. Thompson "plum pudding" model of an atom Taken from Wikimedia Commons
Rutherford’s experiment consisted of aiming alpha particles at a thin sheet of gold foil and observing the scattering pattern on a zinc sulfide screen. Rutherford found that while most of the alpha particles weren’t deflected, some were strongly deflected in hyperbolic paths, and a few were even scattered back close to 180^o180o.

Rutherford's experiment Taken from Wikimedia Commons
Rutherford concluded that the atom consisted of mostly empty space, the nucleus was a very small, densely packed, positive charge, and the electrons orbited around the nucleus like planets orbiting the Sun.
His proposition, however, had several major problems:
- It didn’t account for the appearance of discrete emission line spectra.
- The electrons continuously orbiting the nucleus should've produced a continuous band of electromagnetic radiation, but that doesn’t happen.
- The predicted orbital loss of energy should’ve caused the electron to crash into the nucleus, disintegrating it, but that doesn’t happen,
The Bohr Model
Years after Rutherford’s declaration of his nuclear model of the atom, a physicist named Niels Bohr set out to add an important piece to the atomic puzzle.
Bohr realized that the Balmer formula, which essentially summarizes the visible wavelengths that appear in the emission spectrum of hydrogen, could be looked at in terms of energy differences. The main takeaways:
- Electrons don’t emit electromagnetic radiation while in a given orbit.
- An electron can only have a certain set orbits.
- An atom has definite energy levels analogous to standing waves.

Taken from Wikimedia Commons
Here are some key differences between Bohr and Rutherford's models of the atom:
- Bohr's model:- Proposed that electrons orbit the nucleus in fixed, discrete energy levels- Electrons can only jump between energy levels by absorbing or emitting a specific amount of energy (called a "quantum")- Explained the observed emission spectra of hydrogen atoms
- Rutherford's model:- Proposed that the atom consists of a small, dense nucleus (made of protons and neutrons) surrounded by electrons- Explained the scattering of alpha particles in gold foil experiments- Led to the discovery of the proton and the concept of the atomic nucleus Overall, Bohr's model was able to explain the behavior of atoms at a more macroscopic level, while Rutherford's model provided a more detailed, microscopic view of the structure of the atom. Both models were important contributions to our understanding of the nature of atoms and the way they behave.
Let’s zoom in really quick on the nucleus of an atom. Aren’t the protons experiencing a repulsive Coulomb’s force from each other? What’s holding the nucleus together? Well, the presence of another fundamental force stronger than Coulomb’s force is the reason: the strong nuclear force (yes, it’s really called that). The strong nuclear force binds the neutrons and protons together; it’s the strongest force in nature.
Okay, now back to the Bohr Model of the Atom. Remember how we said that an electron has a certain set orbit? Well, if the electron absorbs a certain amount of energy, it gets excited to a higher orbit with a greater radius. After some time, it returns to a lower orbit, emitting a photon while doing so. Since each allowed orbit (energy level) has a specific radius and energy, the photons in each jump have only specific wavelengths.
When the excited electron drops from energy level n=jn=j to a lower one, n=in=i, the energy of the photon emitted is the difference between the two energy levels:
E*(emitted photon)*=|ΔE|=E_j-E_i
The wavelength of this photon is
λ=c/f=c/(Ephoton/h)=hc/(Ej-Ei)
where
c= speed of light =3.00*10^8
h= Planck's' constant = 6.6310^-^3^4 Js

Taken from Wikimedia Commons
Let's look at a practice problem together.
(A) Looking at the energy level diagram for hydrogen above (ignore the Ly equations near the arrows), how much energy must a ground-state electron in a hydrogen atom absorb to be excited to the n=3 energy level?
(B) If an electron jumped to n=4 level, what wavelengths are possible for the photon emitted when the electron drops to a lower energy level? In what regions of the EM spectrum do these photons lie?
(A)
The ground state energy level (n=1) is -13.6 eV and E_3=-1.51 eV.
The energy needed for an electron to jump from E1 to E3:
E_3-E_1=(-1.51 eV)-(-13.6 eV)= 12.09
(B) An electron in the n=4 energy level can drop to n=3, n=2, or all the way down to n=1. The energies of the n=2 and n=3n=3 levels are
E_2=1/2^2(-13.6 eV)=-3.4 eV
E_3=1/3^2(-13.6)=-1.5eV
The 3 possible values for the energy of the emitted photon:
E_4_→_3=E_4-E_3=(-0.85 eV)-(-1.5 eV)=0.65eV
E_4_→_2=E_4-E_2=(-0.85 eV)-(-3.4 eV)=2.55eV
E_4_→_1=E_4-E_1=(-0.85 eV)-(-13.6 eV) 12.8 eV
From the equation E=hf=hc/λ, we get λ=hc/E
λ_4_→_3=(4.1410^-^1^5 eVs)(3.00*10^8 m/s)/(0.65 eV)= 1,910 nm
➡️ In the visible light spectrum; the wavelength matches to the color blue-green
λ_4_→_2=(4.1410^-^1^5 eVs)(3.00*10^8 m/s)/(2.55 eV)=487 nm
➡️ Ultraviolet wavelength
λ_4_→_1=(4.1410^-^1^5 eVs)(3.00*10^8 m/s)/(12.8 eV)=97 nm
➡️Infrared
Practice Problems
- According to the Bohr theory of the hydrogen atom, electrons starting in the 4th energy level and eventually ending up in the ground state, could produce a total of how many lines in the hydrogen spectra?
A) 7
B) 6
C) 5
D) 4
E) 3
- In Rutherford's famous gold foil scattering experiment, he found that most alpha particles would pass through the foil undeflected. Which of the following nuclear properties can be inferred from this observation?
A) The nucleus must have a positive charge
B) Most of the mass of an atom is in the nucleus
C) The nucleus contains both protons and neutrons
D) The diameter of the nucleus is small compared to the diameter of the atom
E) none of the above.
- According to the Bohr model of the atom, electrons orbit the nucleus in definite orbits. According to the laws of classical physics, this model would be impossible because
A) the positively charged nucleus attracts the electrons
B) Coulomb's law applies
C) accelerating electrons radiate energy
D) there is a centripetal force on the electrons
E) angular momentum is conserved

- A hypothetical atom has four energy states as shown.Which of the following photon energies could NOT be found in the emission spectra of this atom after it has been excited to the n = 4 state?
A) 1 eV
B) 2 eV
C) 3 eV
D) 4 eV
E) 5 eV
- Which of the following transitions will produce the photon with the longest wavelength?
A) n = 2 to n = 1
B) n = 3 to n = 1
C) n = 3 to n = 2
D) n = 4 to n = 1
E) n = 4 to n = 3
Answers:
- B: 4–3, 3–2, 2–1 … or 4–2, 2–1 … or 4–3, 3–1 … or 4–1 … this is a total of 6 different transitions.
- D: While Rutherford’s experiment did show most of these, looking at the single fact provided (that most particles pass straight through) only meant that most of the atom was empty space and that the nucleus must be small.
- C: According to classical physics, when charges accelerate in circles, they necessarily radiate energy in the form of light. This would cause them to spiral into the nucleus as they radiate continuous spectrums of color. This does not happen though, which is a flaw in the Rutherford model
- D: Electron jumps could happen as follows 4–3, 3–2, 2–1 … or 4–2, 2–1 … or 4–3, 3–1 … or 4–1.In these emissions from the differences in the energy level graph, we can make all of the energy difference choices except 4 eV.
- E: Big λ means the least energy based on E=hc/ λ. The least energy corresponds to the smallest energy level jump which is 4–3.

© 2024 Fiveable Inc. All rights reserved.