Browse By Unit
6.1 Simple Harmonic Motion, Springs, and Pendulums
4 min read•june 18, 2024
Daniella Garcia-Loos
Daniella Garcia-Loos
SHM, Periodic Motion, and Examples 🕰️
Simple harmonic motion (SHM) is a type of periodic motion where an object oscillates about a fixed point (equilibrium position) with a constant amplitude and frequency. The motion of the object is described by a sine or cosine function and is characterized by a restoring force that is proportional to the displacement of the object from the equilibrium position. Here are some key points about simple harmonic motion:
- The restoring force is always directed towards the equilibrium position and is proportional to the displacement. The proportionality constant is called the spring constant (k)
- The displacement of the object from the equilibrium position is given by x(t) = A*cos(wt + φ) where A is the amplitude, w is the angular frequency, and φ is the phase angle
- The angular frequency (w) and the period (T) of the motion are related by the equation w = 2π/T. The frequency (f) is the reciprocal of the period (f = 1/T)
- The velocity and acceleration of the object also have a sinusoidal form, and the maximum velocity and acceleration occur at the equilibrium position.
- The energy of the object oscillating in simple harmonic motion is a combination of potential energy (elastic energy stored in the spring) and kinetic energy.
- Simple harmonic motion can be seen in many physical systems, such as a mass attached to a spring, a pendulum, and oscillations of an electric circuit.
- Any physical system that creates a linear restoring force will exhibit the characteristics of SHM.
- It's important to note that the SHM is an idealized concept, in many real-world situations the motion may deviate from the SHM due to factors like damping (friction) and external forces.
Let's begin by defining what simple harmonic motion is!
Firstly, periodic motion is the type of motion that repeats itself over and over.
Simple Harmonic Motion is periodic motion that follows this very general equation:

Where x is position as a function of time, A is the amplitude of the wave function, omega is angular frequency, and phi is the phase shift/angle.
Additionally, we can find equations to describe velocity and acceleration in simple harmonic motion by taking derivatives! Which gives us:
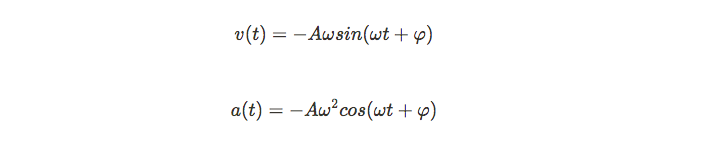
Let's take a look at some graphs depicting these relationships!
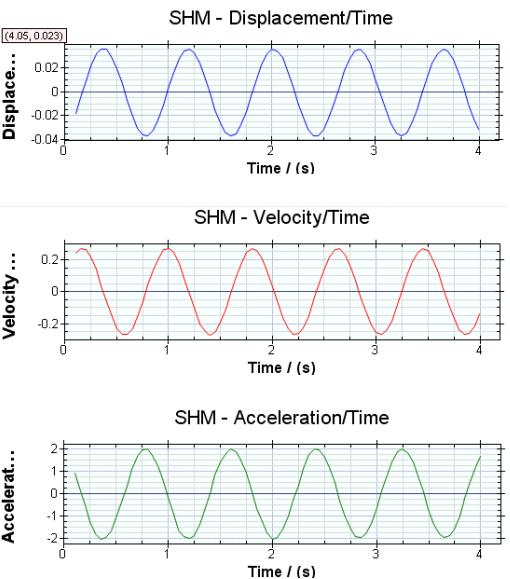
Image taken from Physics Stack Exchange
You should be able to notice the calculus-based relationships between the slopes, where they should be zero, where directions are changing, and where the equations are reaching local maxima/minima.
Now, let's discuss a common part of a wave function. Since we have angular frequency, we can also describe simple harmonic motion with a period.
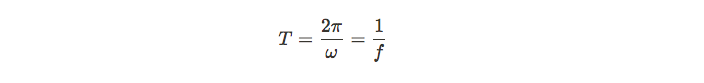
I bet you thought the calculus was over, get ready for the generic differential equation version of simple harmonic motion!
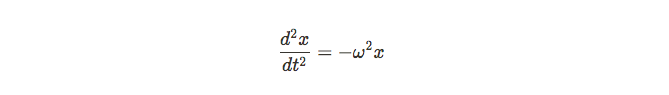
This equation stems from Newton's Second Law (which I'll show later) and can be used to describe any simple harmonic motion (SHM) scenario. If something is in SHM, it should be able to be described in a manner similar to this. X does not necessarily need to be displacement or distance for it to be applicable, it could be theta or arc length, or any other crazy unit of measurement!
Let's try to find period using the relationship above for two common SHM scenarios: springs and pendulums.
Springs:

There we have it! This should look similar to something in your formula chart.
⚠️Note: Any system that creates a linear restoring force (F=-kx) will display the characteristics of SHM!
Pendulums:
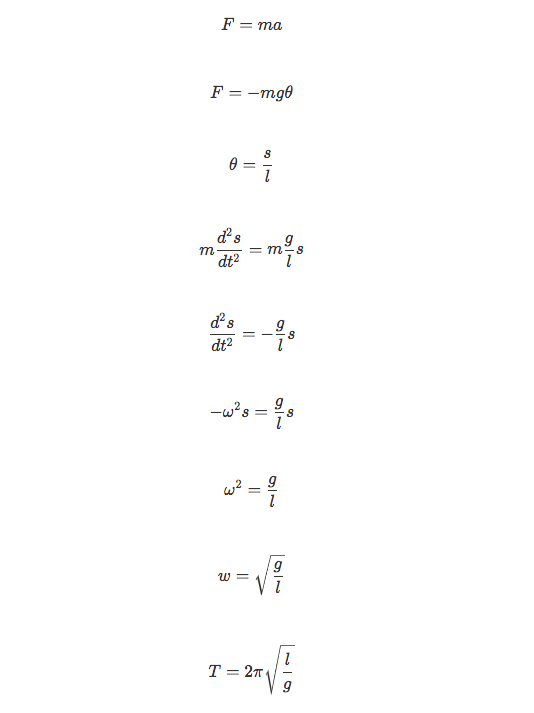
Which is another formula you should be familiar with!
You didn't think we forgot about energy did you? Let's analyze some relationships in SHM with energy!
Total mechanical energy in SHM is always conserved, and it is the sum of the kinetic energy and potential energy(which comes from the restoring force, like gravity or spring).
ME = K + U
in which kinetic energy is:
K = .5mv^2
and potential energy is
Us = .5kx^2 or Ug = mgh
Let's take a look at a graph representing these relationships:
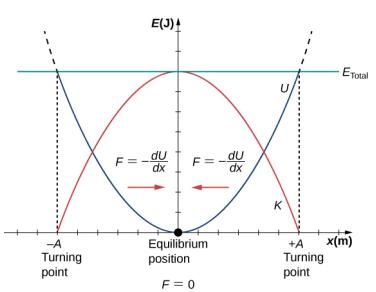
Image taken from LibreTexts
As you can see, the maximum potential energy occurs at maximum displacement, in which velocity is zero and kinetic energy is zero because the object is changing directions. Kinetic energy is at its maximum at the equilibrium position where velocity is at its max and displacement is zero.
Practice Questions

Taken from College Board
Answers
The beginning of this FRQ involves the application of previous units, like momentum and energy into an SHM scenario. Then it involves correctly identifying the proper SHM formula from the formula chart.

The next two parts involve recognizing relationships in equations! From a simple increase or decrease in accordance to another variable, to finding local maxima and minima, you should be prepared to analyze SHM situations in the context of calculus.

<< Hide Menu
6.1 Simple Harmonic Motion, Springs, and Pendulums
4 min read•june 18, 2024
Daniella Garcia-Loos
Daniella Garcia-Loos
SHM, Periodic Motion, and Examples 🕰️
Simple harmonic motion (SHM) is a type of periodic motion where an object oscillates about a fixed point (equilibrium position) with a constant amplitude and frequency. The motion of the object is described by a sine or cosine function and is characterized by a restoring force that is proportional to the displacement of the object from the equilibrium position. Here are some key points about simple harmonic motion:
- The restoring force is always directed towards the equilibrium position and is proportional to the displacement. The proportionality constant is called the spring constant (k)
- The displacement of the object from the equilibrium position is given by x(t) = A*cos(wt + φ) where A is the amplitude, w is the angular frequency, and φ is the phase angle
- The angular frequency (w) and the period (T) of the motion are related by the equation w = 2π/T. The frequency (f) is the reciprocal of the period (f = 1/T)
- The velocity and acceleration of the object also have a sinusoidal form, and the maximum velocity and acceleration occur at the equilibrium position.
- The energy of the object oscillating in simple harmonic motion is a combination of potential energy (elastic energy stored in the spring) and kinetic energy.
- Simple harmonic motion can be seen in many physical systems, such as a mass attached to a spring, a pendulum, and oscillations of an electric circuit.
- Any physical system that creates a linear restoring force will exhibit the characteristics of SHM.
- It's important to note that the SHM is an idealized concept, in many real-world situations the motion may deviate from the SHM due to factors like damping (friction) and external forces.
Let's begin by defining what simple harmonic motion is!
Firstly, periodic motion is the type of motion that repeats itself over and over.
Simple Harmonic Motion is periodic motion that follows this very general equation:

Where x is position as a function of time, A is the amplitude of the wave function, omega is angular frequency, and phi is the phase shift/angle.
Additionally, we can find equations to describe velocity and acceleration in simple harmonic motion by taking derivatives! Which gives us:
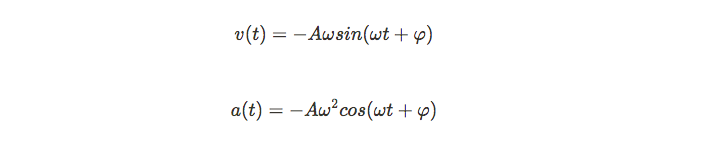
Let's take a look at some graphs depicting these relationships!

Image taken from Physics Stack Exchange
You should be able to notice the calculus-based relationships between the slopes, where they should be zero, where directions are changing, and where the equations are reaching local maxima/minima.
Now, let's discuss a common part of a wave function. Since we have angular frequency, we can also describe simple harmonic motion with a period.
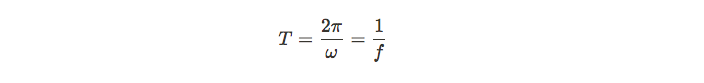
I bet you thought the calculus was over, get ready for the generic differential equation version of simple harmonic motion!
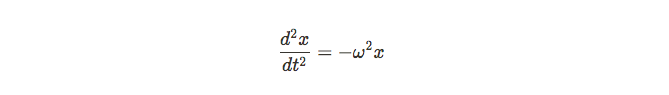
This equation stems from Newton's Second Law (which I'll show later) and can be used to describe any simple harmonic motion (SHM) scenario. If something is in SHM, it should be able to be described in a manner similar to this. X does not necessarily need to be displacement or distance for it to be applicable, it could be theta or arc length, or any other crazy unit of measurement!
Let's try to find period using the relationship above for two common SHM scenarios: springs and pendulums.
Springs:

There we have it! This should look similar to something in your formula chart.
⚠️Note: Any system that creates a linear restoring force (F=-kx) will display the characteristics of SHM!
Pendulums:
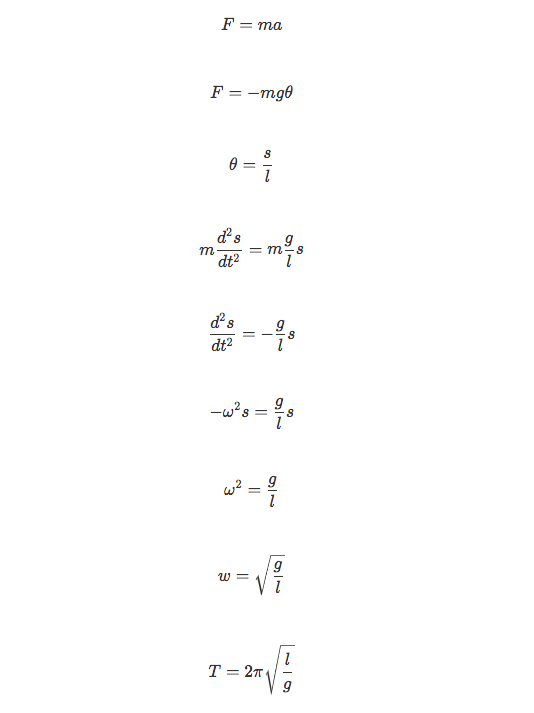
Which is another formula you should be familiar with!
You didn't think we forgot about energy did you? Let's analyze some relationships in SHM with energy!
Total mechanical energy in SHM is always conserved, and it is the sum of the kinetic energy and potential energy(which comes from the restoring force, like gravity or spring).
ME = K + U
in which kinetic energy is:
K = .5mv^2
and potential energy is
Us = .5kx^2 or Ug = mgh
Let's take a look at a graph representing these relationships:

Image taken from LibreTexts
As you can see, the maximum potential energy occurs at maximum displacement, in which velocity is zero and kinetic energy is zero because the object is changing directions. Kinetic energy is at its maximum at the equilibrium position where velocity is at its max and displacement is zero.
Practice Questions

Taken from College Board
Answers
The beginning of this FRQ involves the application of previous units, like momentum and energy into an SHM scenario. Then it involves correctly identifying the proper SHM formula from the formula chart.

The next two parts involve recognizing relationships in equations! From a simple increase or decrease in accordance to another variable, to finding local maxima and minima, you should be prepared to analyze SHM situations in the context of calculus.


© 2024 Fiveable Inc. All rights reserved.