Browse By Unit
1.1 Change in Tandem
A Refresher on Functions
In algebra or even geometry, you might recall the word “function.” No, no, no, not like a family or friendsgiving function. A mathematical function! 🥧
A function is a fundamental concept that describes a relationship between two sets of values, where each input value from the first set, known as the domain, is associated with one and only one output value from the second set, called the range.
You can think of a function as a machine that takes in input values and produces output values according to a set of rules or a formula. These rules or formulae can be as simple as adding or subtracting numbers, or as complex as solving differential equations or integrating functions in calculus.
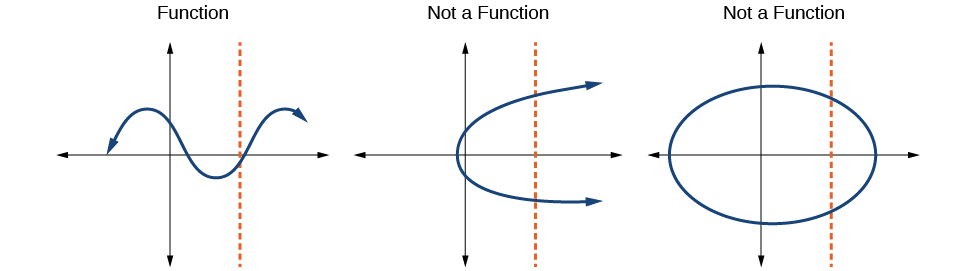
Image Courtesy of Phil Schatz
The domain of a function refers to the set of all possible input values that the function can take, while the range refers to the set of all possible output values that the function can produce. It is important to note that not all sets of input values will produce a valid output, and that the domain may need to be restricted to ensure that the function produces meaningful results. ⛳
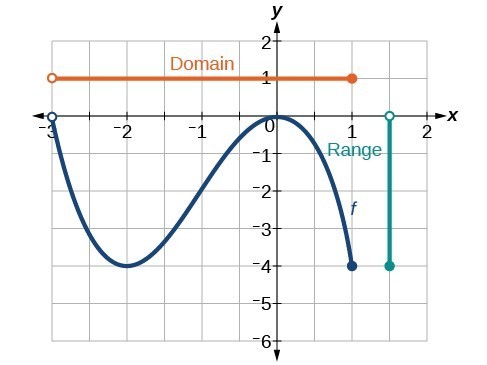
Image Courtesy of Lumen Learning
Variables
The independent variable is the input value, or the value that is changed or controlled in a given situation. It is called "independent" because it is not affected by any other variable in the relationship.
On the other hand, the dependent variable is the output value, or the value that depends on the independent variable. It is called "dependent" because it is affected by the value of the independent variable.
To put it in simpler terms, think of the independent variable as the cause, and the dependent variable as the effect. The independent variable is the factor that causes changes in the dependent variable. 👍
For example, if we have a function that describes the relationship between the time spent studying and the grade received on a test, then the time spent studying is the independent variable, and the grade received on the test is the dependent variable. The time spent studying is what causes changes in the grade received on the test.
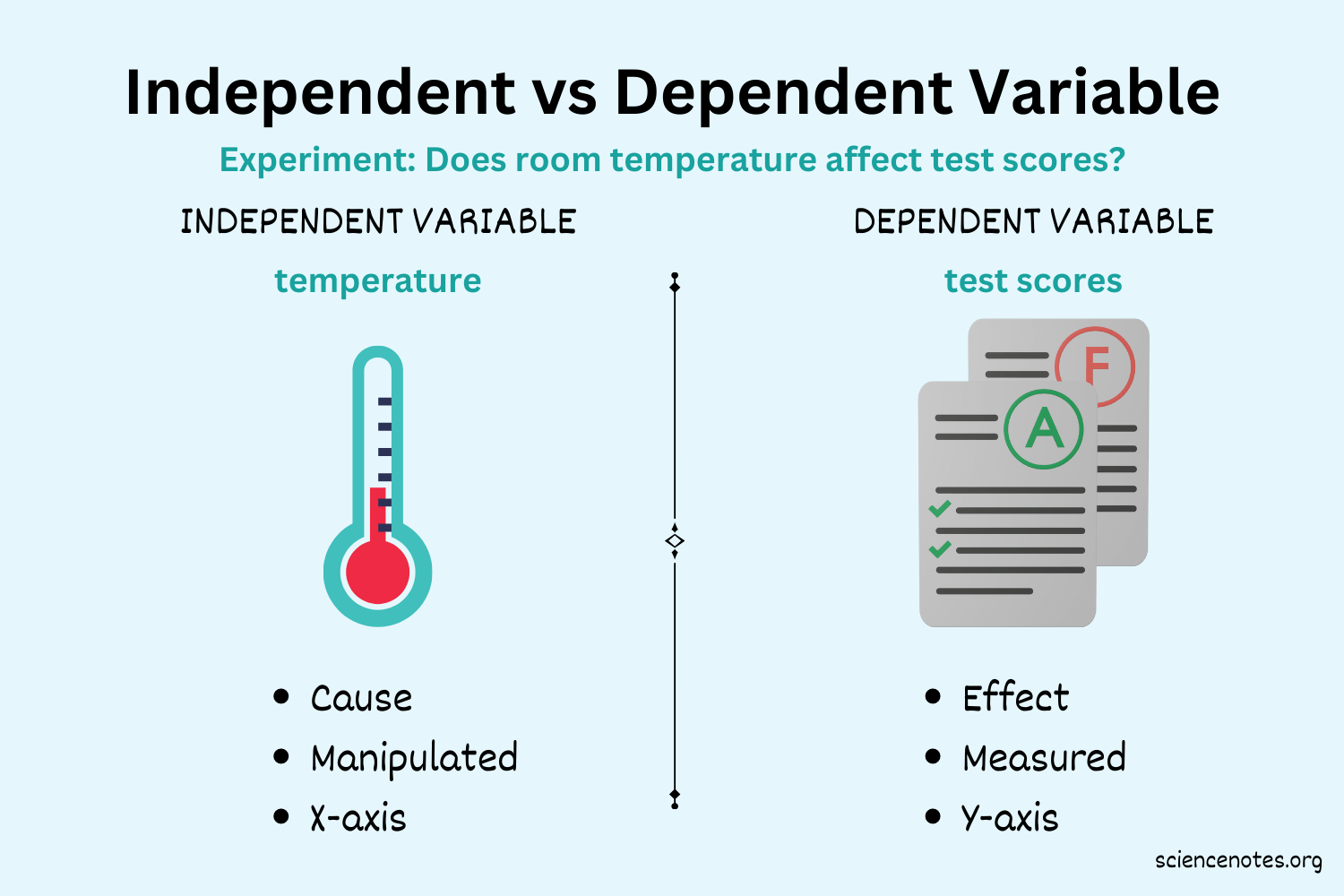
Image Courtesy of Science Notes
The Function Rule
The relationship between the input and output values is determined by the function rule, which specifies how the input values are transformed into output values. 📐
The function rule can be expressed in various ways, such as graphically, numerically, analytically, or verbally. Graphical representation involves plotting the input and output values on a coordinate plane to create a graph that shows the shape and characteristics of the function.
- Numerical representation involves listing the input and output values in a table or sequence to show the pattern of the function.
- Analytical representation involves using a formula or equation to express the function rule mathematically. This allows us to manipulate and analyze the function algebraically, and to make predictions about the behavior of the function under different conditions.
- Verbal representation involves describing the function rule in words, which can be useful for interpreting and communicating the meaning of the function in everyday language.
Increasing vs. Decreasing Functions
Increasing functions has output values increase as the input values increase. More formally, we say that a function f(x) is increasing over an interval [a, b] of its domain if for any two values a and b in the interval, with a < b, we have f(a) < f(b).
To understand this definition, consider a simple example of an increasing function, such as f(x) = x. This function takes any input value x and returns the same value as the output. As we move from left to right along the x-axis, the function values increase at a constant rate. For example, f(0) = 0, f(1) = 1, f(2) = 2, and so on. This means that the function is increasing over its entire domain.
Another example of an increasing function is the exponential function, f(x) = . This function grows exponentially as the input values increase, which means that its output values increase even faster than the input values. For example, f(0) = 1, f(1) = e, f(2) = , and so on. Again, we see that the function is increasing over its entire domain.
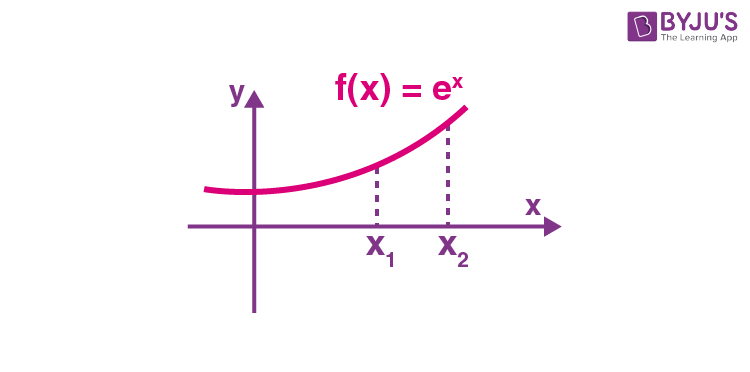
Image Courtesy of Byjus
Decreasing functions has output values decrease as the input values increase. More formally, we say that a function f(x) is decreasing over an interval [a, b] of its domain if for any two values a and b in the interval, with a < b, we have f(a) > f(b).
To understand this definition, consider a simple example of a decreasing function, such as f(x) = -x. This function takes any input value x and returns the negative of that value as the output. As we move from left to right along the x-axis, the function values decrease at a constant rate. For example, f(0) = 0, f(1) = -1, f(2) = -2, and so on. This means that the function is decreasing over its entire domain.
Another example of a decreasing function is the reciprocal function, f(x) = . This function decreases as the input values increase, which means that its output values decrease even faster than the input values. For example, f(1) = 1, f(2) = 1/2, f(3) = 1/3, and so on. Again, we see that the function is decreasing over its entire domain.
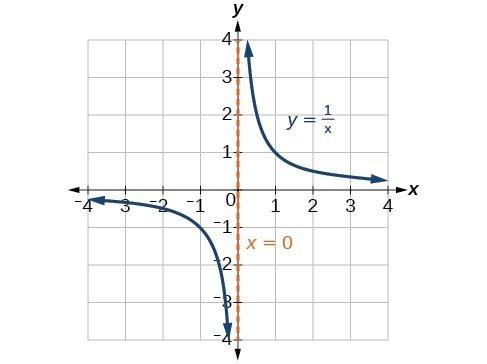
Image Courtesy of Quora
Features of Functions
Concavity
The curvature of a graph, also known as its concavity, is an important characteristic of a function that can reveal information about the function's behavior:
- 🥣 A function is said to be concave up on an interval if its graph curves upward, like the shape of a bowl. This means that the rate of change is increasing.
- ☹️ A function is concave down on an interval if its graph curves downward, like the shape of a frown. This means that the rate of change is decreasing.
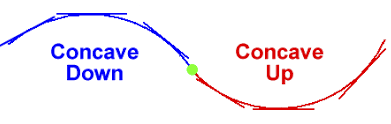
Image Courtesy of Massey University
Zeroes
When the output value of a function is zero, the graph of the function intersects the x-axis. The input values that correspond to these output values are called zeros of the function. 0️⃣
Zeros of a function are also known as roots or solutions of the function. In algebraic terms, finding the zeros of a function means solving the equation f(x) = 0, where f(x) is the function. The solutions to this equation are the values of x that make the output of the function equal to zero.

Image Courtesy of Math Leaks
<< Hide Menu
1.1 Change in Tandem
A Refresher on Functions
In algebra or even geometry, you might recall the word “function.” No, no, no, not like a family or friendsgiving function. A mathematical function! 🥧
A function is a fundamental concept that describes a relationship between two sets of values, where each input value from the first set, known as the domain, is associated with one and only one output value from the second set, called the range.
You can think of a function as a machine that takes in input values and produces output values according to a set of rules or a formula. These rules or formulae can be as simple as adding or subtracting numbers, or as complex as solving differential equations or integrating functions in calculus.

Image Courtesy of Phil Schatz
The domain of a function refers to the set of all possible input values that the function can take, while the range refers to the set of all possible output values that the function can produce. It is important to note that not all sets of input values will produce a valid output, and that the domain may need to be restricted to ensure that the function produces meaningful results. ⛳

Image Courtesy of Lumen Learning
Variables
The independent variable is the input value, or the value that is changed or controlled in a given situation. It is called "independent" because it is not affected by any other variable in the relationship.
On the other hand, the dependent variable is the output value, or the value that depends on the independent variable. It is called "dependent" because it is affected by the value of the independent variable.
To put it in simpler terms, think of the independent variable as the cause, and the dependent variable as the effect. The independent variable is the factor that causes changes in the dependent variable. 👍
For example, if we have a function that describes the relationship between the time spent studying and the grade received on a test, then the time spent studying is the independent variable, and the grade received on the test is the dependent variable. The time spent studying is what causes changes in the grade received on the test.

Image Courtesy of Science Notes
The Function Rule
The relationship between the input and output values is determined by the function rule, which specifies how the input values are transformed into output values. 📐
The function rule can be expressed in various ways, such as graphically, numerically, analytically, or verbally. Graphical representation involves plotting the input and output values on a coordinate plane to create a graph that shows the shape and characteristics of the function.
- Numerical representation involves listing the input and output values in a table or sequence to show the pattern of the function.
- Analytical representation involves using a formula or equation to express the function rule mathematically. This allows us to manipulate and analyze the function algebraically, and to make predictions about the behavior of the function under different conditions.
- Verbal representation involves describing the function rule in words, which can be useful for interpreting and communicating the meaning of the function in everyday language.
Increasing vs. Decreasing Functions
Increasing functions has output values increase as the input values increase. More formally, we say that a function f(x) is increasing over an interval [a, b] of its domain if for any two values a and b in the interval, with a < b, we have f(a) < f(b).
To understand this definition, consider a simple example of an increasing function, such as f(x) = x. This function takes any input value x and returns the same value as the output. As we move from left to right along the x-axis, the function values increase at a constant rate. For example, f(0) = 0, f(1) = 1, f(2) = 2, and so on. This means that the function is increasing over its entire domain.
Another example of an increasing function is the exponential function, f(x) = . This function grows exponentially as the input values increase, which means that its output values increase even faster than the input values. For example, f(0) = 1, f(1) = e, f(2) = , and so on. Again, we see that the function is increasing over its entire domain.
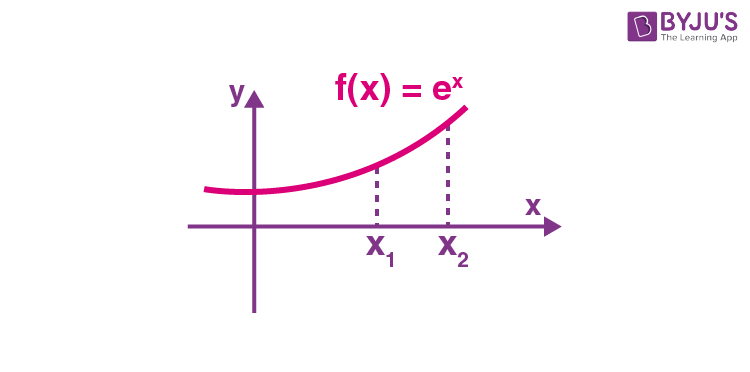
Image Courtesy of Byjus
Decreasing functions has output values decrease as the input values increase. More formally, we say that a function f(x) is decreasing over an interval [a, b] of its domain if for any two values a and b in the interval, with a < b, we have f(a) > f(b).
To understand this definition, consider a simple example of a decreasing function, such as f(x) = -x. This function takes any input value x and returns the negative of that value as the output. As we move from left to right along the x-axis, the function values decrease at a constant rate. For example, f(0) = 0, f(1) = -1, f(2) = -2, and so on. This means that the function is decreasing over its entire domain.
Another example of a decreasing function is the reciprocal function, f(x) = . This function decreases as the input values increase, which means that its output values decrease even faster than the input values. For example, f(1) = 1, f(2) = 1/2, f(3) = 1/3, and so on. Again, we see that the function is decreasing over its entire domain.

Image Courtesy of Quora
Features of Functions
Concavity
The curvature of a graph, also known as its concavity, is an important characteristic of a function that can reveal information about the function's behavior:
- 🥣 A function is said to be concave up on an interval if its graph curves upward, like the shape of a bowl. This means that the rate of change is increasing.
- ☹️ A function is concave down on an interval if its graph curves downward, like the shape of a frown. This means that the rate of change is decreasing.

Image Courtesy of Massey University
Zeroes
When the output value of a function is zero, the graph of the function intersects the x-axis. The input values that correspond to these output values are called zeros of the function. 0️⃣
Zeros of a function are also known as roots or solutions of the function. In algebraic terms, finding the zeros of a function means solving the equation f(x) = 0, where f(x) is the function. The solutions to this equation are the values of x that make the output of the function equal to zero.

Image Courtesy of Math Leaks

© 2024 Fiveable Inc. All rights reserved.