Browse By Unit
1.5 Polynomial Functions and Complex Zeros
1 min read•june 18, 2024
1.5 Polynomial Functions and Complex Zeros
Let’s dive deeper into the polynomial rabbit hole, shall we? This time, we’ll have to work with both complex and real numbers to deal with zeros, multiplicities, degrees, and oddness (or even-ness) of polynomial functions! 🐰
🔢 Real, Imaginary, and Complex Numbers
Real Numbers
Real numbers are numbers that can be expressed as a single point on the number line. They include all rational and irrational numbers, such as integers, fractions, decimals, and square roots. Real numbers can be positive, negative, or zero.
Examples of real numbers include:
- 2
- 3.14
- 1/2
- √5 (which is an irrational number)
Imaginary Numbers
Imaginary numbers are numbers that can be expressed as the product of a real number and the imaginary unit "i", which is defined as the square root of -1. Imaginary numbers are typically written in the form bi, where b is a real number.
Examples of imaginary numbers include:
- 2i
- 3.5i
- (1/2)i
- √7i (which is a complex number with a non-zero imaginary part and zero real part)
Complex Numbers
Complex numbers, on the other hand, are numbers that can be expressed as a sum of a real part and an imaginary part. Again, the imaginary part is a multiple of the imaginary unit "i", which is defined as the square root of -1. Complex numbers are typically written in the form a + bi, where a and b are real numbers.
Examples of complex numbers include:
- 3 + 4i
- 2i
- 1/2 + 2i
- √3 - i (which is a complex number with a non-zero real and imaginary part)

Image Courtesy of Brilliant
Linear Factors and Multiplicities
A complex number "a" is said to be a zero of a polynomial function "p" if evaluating "p(a)" gives a result of zero. In other words, "a" is a root of the polynomial equation p(x) = 0. If a is a real number, then the linear factor (x - a) is a factor of p if and only if a is a zero of p. 👌
This means that for any polynomial function with complex coefficients, its zeros or roots can be complex numbers. However, if the polynomial function has only real coefficients, then complex zeros must occur in conjugate pairs, meaning that if a + bi is a zero of the polynomial function, then its complex conjugate a - bi must also be a zero.
Furthermore, a real zero of a polynomial function must always correspond to a linear factor of the polynomial, which can be expressed as (x - a) where a is the real zero. 0️⃣
If a polynomial function p(x) has a repeated linear factor of the form (x - a) raised to the power n, then a is a zero of multiplicity n. This means that when p(x) is factored, there will be n identical linear factors of the form (x - a).
For a polynomial function of degree n, which means that the highest power of x in p(x) is n, the function will have exactly n complex zeros when counting multiplicities. This means that if a zero has multiplicity m, then it will be counted m times when counting the total number of zeros of p(x).
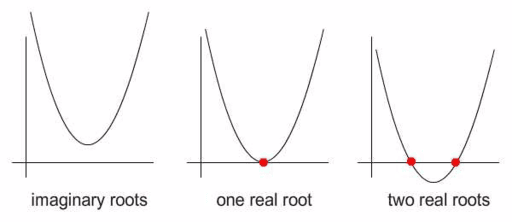
Image Courtesy of GeoGebra
🙅🏻 X-Intercepts
If a polynomial function p(x) has a real zero at a, then the graph of the function intersects the x-axis at the point (a, 0). This means that the value of p(a) is zero, so the point (a, 0) lies on the graph of p(x). 💪
Consequently, the real zeros of a polynomial can be used to find intervals on the x-axis where p(x) is either positive or negative. For example, if p(x) has a real zero at a, then the function changes sign at a. This means that if we choose a test point to the left of a, then p(x) will be negative to the left of a and positive to the right of a. ↔️
Similarly, if we choose a test point to the right of a, then p(x) will be positive to the left of a and negative to the right of a. By using the real zeros of p(x) as endpoints for these intervals, we can determine where the function is positive or negative for all values of x.
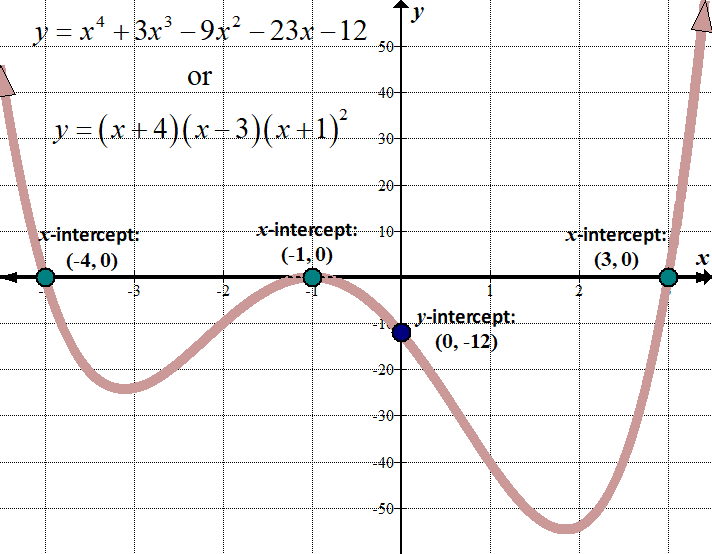
Image Courtesy of Math Hints
✌🏼 Even Multiplicities
When a polynomial function p(x) has a real zero at "a" with an even multiplicity, it means that the factor (x - a) appears twice or more times in the factored form of p(x). In this case, the behavior of p(x) around the zero a is characterized by the fact that the signs of the output values of p(x) will be the same for input values near x = a.
This behavior is reflected in the graph of p(x) near the zero a. Specifically, when the multiplicity of the zero is even, the graph of p(x) will be tangent to the x-axis at x = a. This is because the function changes sign at the zero, but since the multiplicity is even, it does not cross the x-axis at that point. ❌

Image Courtesy of Lumen Learning
Instead, the graph touches the x-axis at x = a and turns around, remaining on the same side of the x-axis. The fact that the signs of the output values of p(x) are the same for input values near x = a is what makes this behavior possible! 🤓
Working with Polynomial Functions
🧐 Determining Degree of Polynomial Functions
To determine the degree of a polynomial function p(x), we can examine the pattern of differences between the output values of p(x) for equal-interval input values. Specifically, we compute the first differences, second differences, third differences, and so on, until we find a constant value for some nth difference. ➖
The degree of p(x) is then equal to the least value n for which the successive nth differences are constant. In other words, if we compute the first differences and they are not constant, we continue to compute the second differences. If the second differences are not constant, we compute the third differences, and so on, until we find a constant value. ✏️
For example, if the first differences are constant, then p(x) is a linear function and has degree 1. If the second differences are constant, then p(x) is a quadratic function and has degree 2. If the third differences are constant, then p(x) is a cubic function and has degree 3, and so on.
This method for finding the degree of a polynomial function is known as the method of successive differences. It’s very useful because it can be applied to any polynomial function, regardless of its form or complexity. 🤩
Finding the Degree of Polynomials Practice Question
Let’s take a look at a sample question!
Suppose we have the polynomial function . We want to find the degree of this polynomial using the method of successive differences.
To do this, we first compute the first differences between the output values of "p(x)" for consecutive input values:
We see that the first differences are not constant, so we proceed to compute the second differences:
Again, the second differences are not constant, so we compute the third differences:
We finally see that the third differences are constant at 12. Therefore, the degree of p(x) is equal to 3, since this is the least value of "n" for which the successive nth differences are constant. We can conclude that "p(x)" is a cubic polynomial function.
Distinguishing Polynomial Functions: Even Functions
An even function has two important properties.
- It is graphically symmetric over the line x = 0, which means that if we reflect the graph of the function across the y-axis, we obtain the same graph. 🟰
- It satisfies the analytical property f(−x) = f(x), which means that if we replace x with −x in the function, we obtain the same output as when we evaluate the function at x.
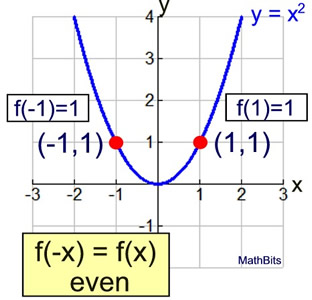
Image Courtesy of Math Bits Notebook
For polynomials, a polynomial of the form , where n is an even positive integer and , is an even function. This is because if we replace x with −x in the polynomial, we obtain: , which shows that the function is indeed even.
In other words, if we graph a polynomial of this form, we will see that it is symmetric over the y-axis, and if we evaluate the polynomial at x and −x, we will obtain the same output.
⤴️ Distinguishing Polynomial Functions: Odd Functions
An odd function has two important properties.
- It is graphically rotationally symmetric about the point (0,0), which means that if we rotate the graph of the function 180 degrees about the origin, we obtain the same graph.
- It satisfies the analytical property f(−x) = −f(x), which means that if we replace x with −x in the function, we obtain the opposite sign of the output as when we evaluate the function at x.

Image Courtesy of Math Bits Notebook
For polynomials, a polynomial of the form , where n is an odd positive integer and , is an odd function. This is because if we replace x with −x in the polynomial, we obtain: which shows that the function is indeed odd.
In other words, if we graph a polynomial of this form, we will see that it is symmetric about the origin, and if we evaluate the polynomial at x and −x, we will obtain opposite sign outputs.
<< Hide Menu
1.5 Polynomial Functions and Complex Zeros
1 min read•june 18, 2024
1.5 Polynomial Functions and Complex Zeros
Let’s dive deeper into the polynomial rabbit hole, shall we? This time, we’ll have to work with both complex and real numbers to deal with zeros, multiplicities, degrees, and oddness (or even-ness) of polynomial functions! 🐰
🔢 Real, Imaginary, and Complex Numbers
Real Numbers
Real numbers are numbers that can be expressed as a single point on the number line. They include all rational and irrational numbers, such as integers, fractions, decimals, and square roots. Real numbers can be positive, negative, or zero.
Examples of real numbers include:
- 2
- 3.14
- 1/2
- √5 (which is an irrational number)
Imaginary Numbers
Imaginary numbers are numbers that can be expressed as the product of a real number and the imaginary unit "i", which is defined as the square root of -1. Imaginary numbers are typically written in the form bi, where b is a real number.
Examples of imaginary numbers include:
- 2i
- 3.5i
- (1/2)i
- √7i (which is a complex number with a non-zero imaginary part and zero real part)
Complex Numbers
Complex numbers, on the other hand, are numbers that can be expressed as a sum of a real part and an imaginary part. Again, the imaginary part is a multiple of the imaginary unit "i", which is defined as the square root of -1. Complex numbers are typically written in the form a + bi, where a and b are real numbers.
Examples of complex numbers include:
- 3 + 4i
- 2i
- 1/2 + 2i
- √3 - i (which is a complex number with a non-zero real and imaginary part)

Image Courtesy of Brilliant
Linear Factors and Multiplicities
A complex number "a" is said to be a zero of a polynomial function "p" if evaluating "p(a)" gives a result of zero. In other words, "a" is a root of the polynomial equation p(x) = 0. If a is a real number, then the linear factor (x - a) is a factor of p if and only if a is a zero of p. 👌
This means that for any polynomial function with complex coefficients, its zeros or roots can be complex numbers. However, if the polynomial function has only real coefficients, then complex zeros must occur in conjugate pairs, meaning that if a + bi is a zero of the polynomial function, then its complex conjugate a - bi must also be a zero.
Furthermore, a real zero of a polynomial function must always correspond to a linear factor of the polynomial, which can be expressed as (x - a) where a is the real zero. 0️⃣
If a polynomial function p(x) has a repeated linear factor of the form (x - a) raised to the power n, then a is a zero of multiplicity n. This means that when p(x) is factored, there will be n identical linear factors of the form (x - a).
For a polynomial function of degree n, which means that the highest power of x in p(x) is n, the function will have exactly n complex zeros when counting multiplicities. This means that if a zero has multiplicity m, then it will be counted m times when counting the total number of zeros of p(x).

Image Courtesy of GeoGebra
🙅🏻 X-Intercepts
If a polynomial function p(x) has a real zero at a, then the graph of the function intersects the x-axis at the point (a, 0). This means that the value of p(a) is zero, so the point (a, 0) lies on the graph of p(x). 💪
Consequently, the real zeros of a polynomial can be used to find intervals on the x-axis where p(x) is either positive or negative. For example, if p(x) has a real zero at a, then the function changes sign at a. This means that if we choose a test point to the left of a, then p(x) will be negative to the left of a and positive to the right of a. ↔️
Similarly, if we choose a test point to the right of a, then p(x) will be positive to the left of a and negative to the right of a. By using the real zeros of p(x) as endpoints for these intervals, we can determine where the function is positive or negative for all values of x.

Image Courtesy of Math Hints
✌🏼 Even Multiplicities
When a polynomial function p(x) has a real zero at "a" with an even multiplicity, it means that the factor (x - a) appears twice or more times in the factored form of p(x). In this case, the behavior of p(x) around the zero a is characterized by the fact that the signs of the output values of p(x) will be the same for input values near x = a.
This behavior is reflected in the graph of p(x) near the zero a. Specifically, when the multiplicity of the zero is even, the graph of p(x) will be tangent to the x-axis at x = a. This is because the function changes sign at the zero, but since the multiplicity is even, it does not cross the x-axis at that point. ❌

Image Courtesy of Lumen Learning
Instead, the graph touches the x-axis at x = a and turns around, remaining on the same side of the x-axis. The fact that the signs of the output values of p(x) are the same for input values near x = a is what makes this behavior possible! 🤓
Working with Polynomial Functions
🧐 Determining Degree of Polynomial Functions
To determine the degree of a polynomial function p(x), we can examine the pattern of differences between the output values of p(x) for equal-interval input values. Specifically, we compute the first differences, second differences, third differences, and so on, until we find a constant value for some nth difference. ➖
The degree of p(x) is then equal to the least value n for which the successive nth differences are constant. In other words, if we compute the first differences and they are not constant, we continue to compute the second differences. If the second differences are not constant, we compute the third differences, and so on, until we find a constant value. ✏️
For example, if the first differences are constant, then p(x) is a linear function and has degree 1. If the second differences are constant, then p(x) is a quadratic function and has degree 2. If the third differences are constant, then p(x) is a cubic function and has degree 3, and so on.
This method for finding the degree of a polynomial function is known as the method of successive differences. It’s very useful because it can be applied to any polynomial function, regardless of its form or complexity. 🤩
Finding the Degree of Polynomials Practice Question
Let’s take a look at a sample question!
Suppose we have the polynomial function . We want to find the degree of this polynomial using the method of successive differences.
To do this, we first compute the first differences between the output values of "p(x)" for consecutive input values:
We see that the first differences are not constant, so we proceed to compute the second differences:
Again, the second differences are not constant, so we compute the third differences:
We finally see that the third differences are constant at 12. Therefore, the degree of p(x) is equal to 3, since this is the least value of "n" for which the successive nth differences are constant. We can conclude that "p(x)" is a cubic polynomial function.
Distinguishing Polynomial Functions: Even Functions
An even function has two important properties.
- It is graphically symmetric over the line x = 0, which means that if we reflect the graph of the function across the y-axis, we obtain the same graph. 🟰
- It satisfies the analytical property f(−x) = f(x), which means that if we replace x with −x in the function, we obtain the same output as when we evaluate the function at x.

Image Courtesy of Math Bits Notebook
For polynomials, a polynomial of the form , where n is an even positive integer and , is an even function. This is because if we replace x with −x in the polynomial, we obtain: , which shows that the function is indeed even.
In other words, if we graph a polynomial of this form, we will see that it is symmetric over the y-axis, and if we evaluate the polynomial at x and −x, we will obtain the same output.
⤴️ Distinguishing Polynomial Functions: Odd Functions
An odd function has two important properties.
- It is graphically rotationally symmetric about the point (0,0), which means that if we rotate the graph of the function 180 degrees about the origin, we obtain the same graph.
- It satisfies the analytical property f(−x) = −f(x), which means that if we replace x with −x in the function, we obtain the opposite sign of the output as when we evaluate the function at x.

Image Courtesy of Math Bits Notebook
For polynomials, a polynomial of the form , where n is an odd positive integer and , is an odd function. This is because if we replace x with −x in the polynomial, we obtain: which shows that the function is indeed odd.
In other words, if we graph a polynomial of this form, we will see that it is symmetric about the origin, and if we evaluate the polynomial at x and −x, we will obtain opposite sign outputs.

© 2024 Fiveable Inc. All rights reserved.