Browse By Unit
1.6 Polynomial Functions and End Behavior
1 min read•june 18, 2024
1.6 Polynomial Functions and End Behavior
We’ve gotten the chance to know our good friend (polynomial functions) over the past couple sections, but there’s one more thing to discover about them: their end behavior! 😌
👋🏼 Introducing End Behaviors
The end behavior of a function describes what happens to the output values of the function as the input values approach positive or negative infinity. In other words, it is a way to describe the long-term behavior of the function. ⏱️
For example, for a polynomial function of degree n, the end behavior can be determined by looking at the sign of the leading coefficient (the coefficient of the term with the highest degree).
If the leading coefficient is positive, then the function will increase without bound as x approaches positive or negative infinity. If the leading coefficient is negative, then the function will decrease without bound as x approaches positive or negative infinity.
🔚 End Behaviors in Polynomial Functions
As input values of a nonconstant polynomial function increase without bound, the output values will either increase or decrease without bound. 🪑
If the leading coefficient of the polynomial is positive, then the function will increase without bound as x approaches positive or negative infinity, which is denoted by the mathematical notation lim p(x) = ∞ or lim p(x) = -∞ as x approaches positive infinity. ⬆️
On the other hand, if the leading coefficient of the polynomial is negative, then the function will decrease without bound as x approaches positive or negative infinity, which is denoted by the mathematical notation lim p(x) = ∞ or lim p(x) = -∞ as x approaches negative infinity ⬇️
This behavior is a result of the fact that the power of x in the polynomial term with the highest degree dominates the other terms as x approaches infinity or negative infinity. Therefore, the behavior of the polynomial at infinity is determined by the sign of the leading coefficient and the degree of the polynomial.
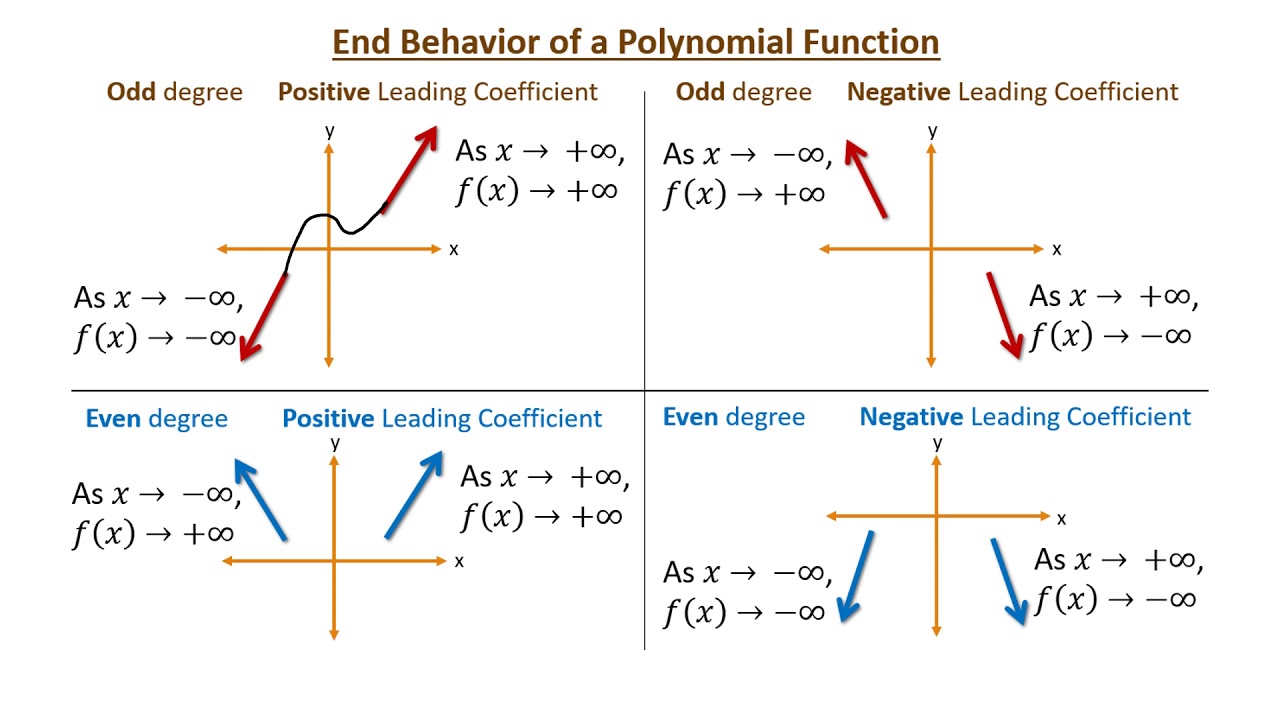
Image Courtesy of MilanVasicMath on YouTube
🤓 Examples of Determining End Behavior
Determining End Behavior: Example 1
Consider the polynomial function .
To determine the end behavior of this function, we need to look at the term with the highest degree, which is . The leading coefficient of this term is positive, which means that as x approaches positive or negative infinity, the value of the function will approach positive infinity for both case. Therefore, the end behavior of is as .
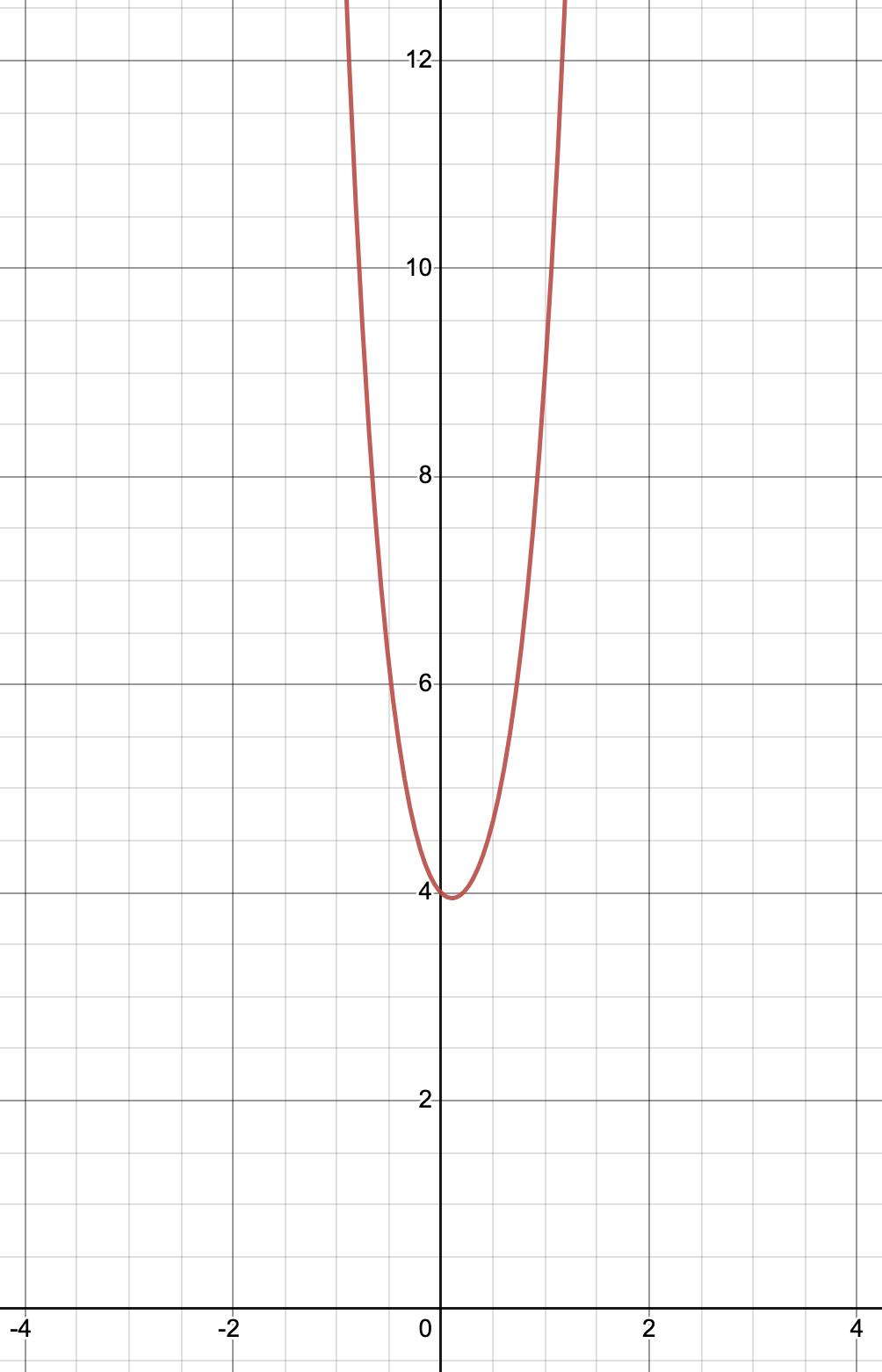
Created by Jed Q on Desmos
Determining End Behavior: Example 2
Now, consider the polynomial function .
In this case, the term with the highest degree is , which has a negative leading coefficient. This means that as x approaches positive or negative infinity, the value of the function will approach negative or positive infinity, respectively. Therefore, the end behavior of is as and as

Created by Jed Q on Desmos
Determining End Behavior: Example 3
Let's examine the polynomial function .
The term with the highest degree is , which has a positive leading coefficient. This means that as approaches positive or negative infinity, the value of the function will approach positive or negative infinity, respectively. Therefore, the end behavior of is as and as

Created by Jed Q on Desmos
Determining End Behavior: Example 4
Finally, let's consider the polynomial function .
Same case as Example 1 but in the opposite direction! In this case, the highest degree term is , which has a negative leading coefficient. Therefore, as x approaches positive or negative infinity, the value of the function will approach negative infinity. Thus, the end behavior of is as

Created by Jed Q on Desmos
<< Hide Menu
1.6 Polynomial Functions and End Behavior
1 min read•june 18, 2024
1.6 Polynomial Functions and End Behavior
We’ve gotten the chance to know our good friend (polynomial functions) over the past couple sections, but there’s one more thing to discover about them: their end behavior! 😌
👋🏼 Introducing End Behaviors
The end behavior of a function describes what happens to the output values of the function as the input values approach positive or negative infinity. In other words, it is a way to describe the long-term behavior of the function. ⏱️
For example, for a polynomial function of degree n, the end behavior can be determined by looking at the sign of the leading coefficient (the coefficient of the term with the highest degree).
If the leading coefficient is positive, then the function will increase without bound as x approaches positive or negative infinity. If the leading coefficient is negative, then the function will decrease without bound as x approaches positive or negative infinity.
🔚 End Behaviors in Polynomial Functions
As input values of a nonconstant polynomial function increase without bound, the output values will either increase or decrease without bound. 🪑
If the leading coefficient of the polynomial is positive, then the function will increase without bound as x approaches positive or negative infinity, which is denoted by the mathematical notation lim p(x) = ∞ or lim p(x) = -∞ as x approaches positive infinity. ⬆️
On the other hand, if the leading coefficient of the polynomial is negative, then the function will decrease without bound as x approaches positive or negative infinity, which is denoted by the mathematical notation lim p(x) = ∞ or lim p(x) = -∞ as x approaches negative infinity ⬇️
This behavior is a result of the fact that the power of x in the polynomial term with the highest degree dominates the other terms as x approaches infinity or negative infinity. Therefore, the behavior of the polynomial at infinity is determined by the sign of the leading coefficient and the degree of the polynomial.

Image Courtesy of MilanVasicMath on YouTube
🤓 Examples of Determining End Behavior
Determining End Behavior: Example 1
Consider the polynomial function .
To determine the end behavior of this function, we need to look at the term with the highest degree, which is . The leading coefficient of this term is positive, which means that as x approaches positive or negative infinity, the value of the function will approach positive infinity for both case. Therefore, the end behavior of is as .

Created by Jed Q on Desmos
Determining End Behavior: Example 2
Now, consider the polynomial function .
In this case, the term with the highest degree is , which has a negative leading coefficient. This means that as x approaches positive or negative infinity, the value of the function will approach negative or positive infinity, respectively. Therefore, the end behavior of is as and as

Created by Jed Q on Desmos
Determining End Behavior: Example 3
Let's examine the polynomial function .
The term with the highest degree is , which has a positive leading coefficient. This means that as approaches positive or negative infinity, the value of the function will approach positive or negative infinity, respectively. Therefore, the end behavior of is as and as

Created by Jed Q on Desmos
Determining End Behavior: Example 4
Finally, let's consider the polynomial function .
Same case as Example 1 but in the opposite direction! In this case, the highest degree term is , which has a negative leading coefficient. Therefore, as x approaches positive or negative infinity, the value of the function will approach negative infinity. Thus, the end behavior of is as

Created by Jed Q on Desmos

© 2024 Fiveable Inc. All rights reserved.