Browse By Unit
1.10 Rational Functions and Holes
1 min read•june 18, 2024
1.10 Rational Functions and Holes
🏌🏽 Hole in One!
The presence of a real zero in both the numerator and denominator of a rational function can have a significant impact on the behavior of the function. If a real number a is a zero of the polynomial function in both the numerator and denominator, then the function has a "hole” at x = a. In other words, the function is undefined at x = a, but it can be "repaired" by canceling out the common factor of (x - a) in the numerator and denominator. ⛳
If the multiplicity of the real zero a in the numerator is greater than or equal to its multiplicity in the denominator, then the function has a hole at x = a. The multiplicity of a zero refers to the number of times it appears in the factorization of the polynomial. For example, if a is a zero of multiplicity 3 in the numerator and multiplicity 2 in the denominator, then the function will have a hole at x = a.
To find the y-value of the hole, we can simply evaluate the function after canceling out the common factor of (x - a). For example, consider the rational function:
r(x) = (x² - 9) / (x - 3)
The polynomial function in the numerator has real zeros at x = -3 and x = 3, and the polynomial function in the denominator has a real zero at x = 3. The multiplicity of the zero at x = 3 in the numerator is 2, which is greater than its multiplicity of 1 in the denominator. Therefore, the function has a hole at x = 3.
To find the y-value of the hole, we can cancel out the common factor of (x - 3) in the numerator and denominator:
r(x) = (x + 3)(x - 3) / (x - 3)
Simplifying this expression, we get:
r(x) = x + 3
Therefore, the function has a hole at x = 3 with a y-value of 6. 🤓
Source: Jed Q
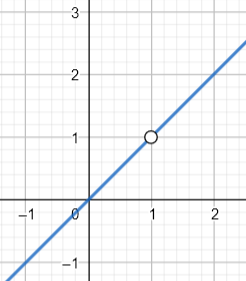
🌉 Connecting to Limits
A rational function, r, may have a hole at x = c. To determine the location of the hole, one can examine the output values that correspond to input values close to c. If the output values are arbitrarily close to some limit L, then the hole is located at the point with coordinates (c, L). This can be expressed mathematically as lim r(x) = L as x approaches c. It is important to note that the limit from the left, right, and as x approaches c are all equal to L.
In other words, if a rational function has a hole at x = c, then the function approaches a finite limit as x approaches c. The value of this limit corresponds to the y-coordinate of the hole. To determine the x-coordinate, one can simply identify the value of c where the hole occurs. 🔍
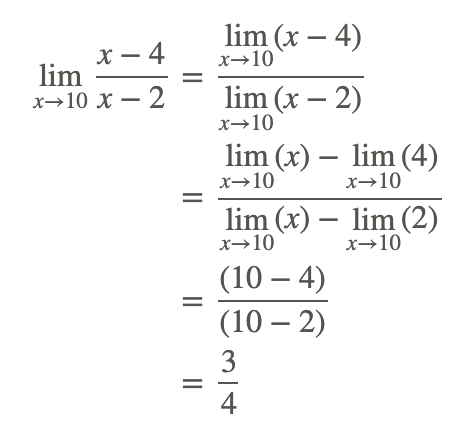
Source: K12 Libretexts
<< Hide Menu
1.10 Rational Functions and Holes
1 min read•june 18, 2024
1.10 Rational Functions and Holes
🏌🏽 Hole in One!
The presence of a real zero in both the numerator and denominator of a rational function can have a significant impact on the behavior of the function. If a real number a is a zero of the polynomial function in both the numerator and denominator, then the function has a "hole” at x = a. In other words, the function is undefined at x = a, but it can be "repaired" by canceling out the common factor of (x - a) in the numerator and denominator. ⛳
If the multiplicity of the real zero a in the numerator is greater than or equal to its multiplicity in the denominator, then the function has a hole at x = a. The multiplicity of a zero refers to the number of times it appears in the factorization of the polynomial. For example, if a is a zero of multiplicity 3 in the numerator and multiplicity 2 in the denominator, then the function will have a hole at x = a.
To find the y-value of the hole, we can simply evaluate the function after canceling out the common factor of (x - a). For example, consider the rational function:
r(x) = (x² - 9) / (x - 3)
The polynomial function in the numerator has real zeros at x = -3 and x = 3, and the polynomial function in the denominator has a real zero at x = 3. The multiplicity of the zero at x = 3 in the numerator is 2, which is greater than its multiplicity of 1 in the denominator. Therefore, the function has a hole at x = 3.
To find the y-value of the hole, we can cancel out the common factor of (x - 3) in the numerator and denominator:
r(x) = (x + 3)(x - 3) / (x - 3)
Simplifying this expression, we get:
r(x) = x + 3
Therefore, the function has a hole at x = 3 with a y-value of 6. 🤓

Source: Jed Q
🌉 Connecting to Limits
A rational function, r, may have a hole at x = c. To determine the location of the hole, one can examine the output values that correspond to input values close to c. If the output values are arbitrarily close to some limit L, then the hole is located at the point with coordinates (c, L). This can be expressed mathematically as lim r(x) = L as x approaches c. It is important to note that the limit from the left, right, and as x approaches c are all equal to L.
In other words, if a rational function has a hole at x = c, then the function approaches a finite limit as x approaches c. The value of this limit corresponds to the y-coordinate of the hole. To determine the x-coordinate, one can simply identify the value of c where the hole occurs. 🔍
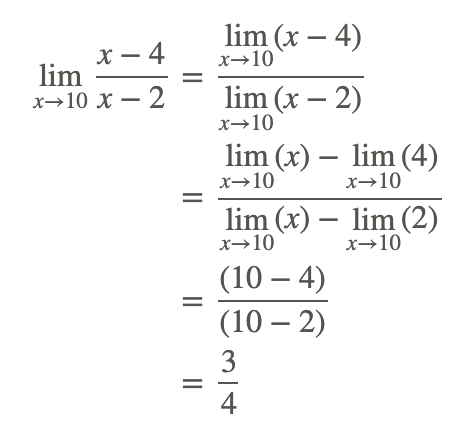
Source: K12 Libretexts

© 2024 Fiveable Inc. All rights reserved.