Browse By Unit
2.1 Change in Arithmetic and Geometric Sequences
1 min read•june 18, 2024
2.1 Change in Arithmetic and Geometric Sequences
A sequence is a function from the whole numbers to the real numbers. This means that, a sequence takes a whole number (say, "n") and assigns it a real number. For example, think of a sequence of your class schedule, Monday is the first day, Tuesday the second, and so on. Each day of the week is assigned a number, Monday is 1, Tuesday is 2, and so on. 💯
Consequently, the graph of a sequence consists of discrete points instead of a curve. This is because in a sequence, we are only dealing with whole numbers, not with a continuous range of numbers like in a function. So, instead of having a smooth curve, we have a set of distinct points on a graph. 📌
For example, you might want to track the number of hours of sleep you get each night. You start on Monday and get 8 hours of sleep, on Tuesday you get 6 hours of sleep, on Wednesday you get 7 hours of sleep and so on. This is a sequence, where the input variable is the day of the week and the output variable is the number of hours of sleep. If we graph this, we would get a set of discrete points on a graph, one for each day of the week, instead of a smooth curve. 😴
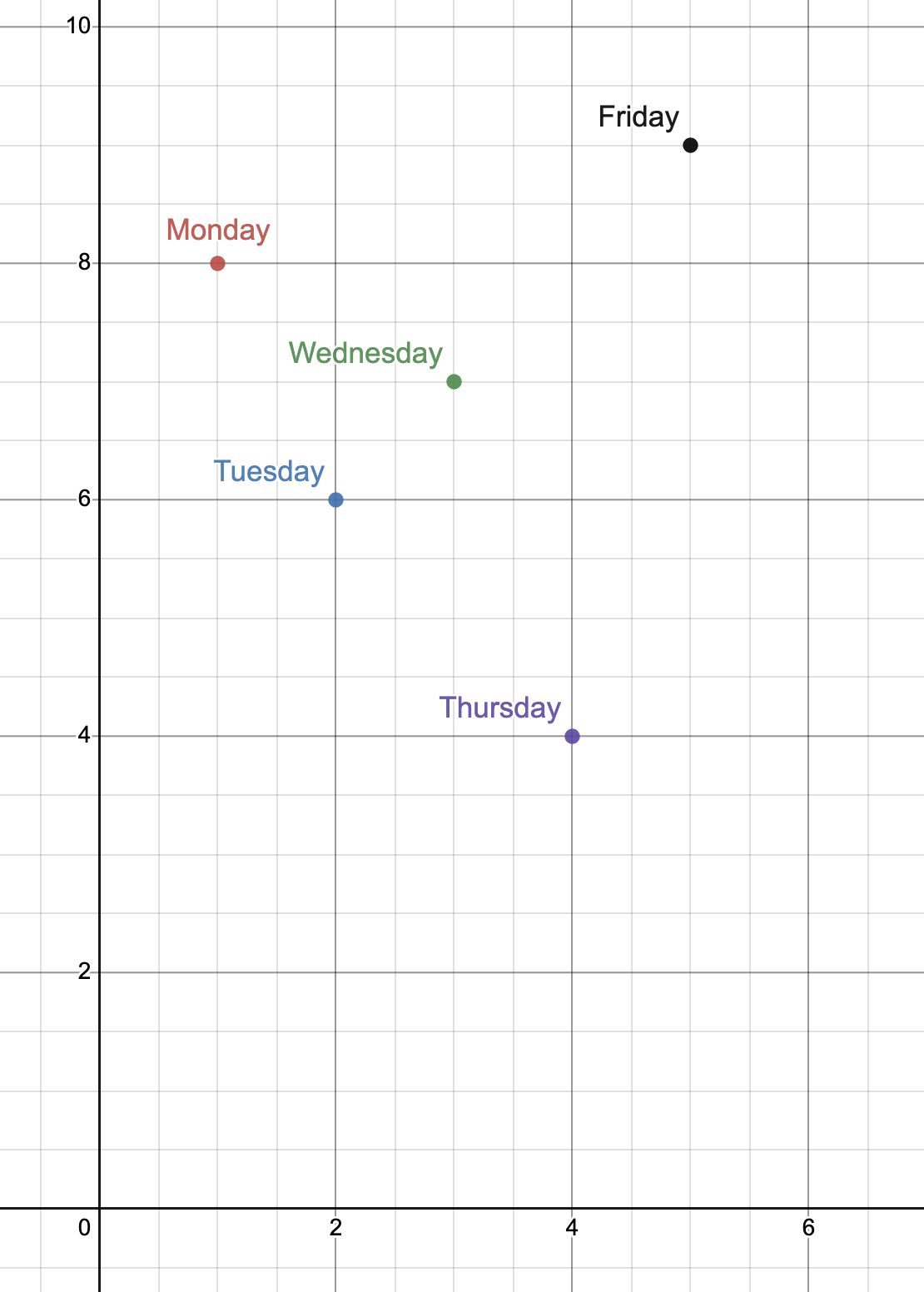
Source: Desmos Graphing Calculator
Again, we’re looking at discrete points—don’t connect the dots like you’d typically do to draw a curve! Note that the sequence above is just a regular ol’ sequence (not an arithmetic or geometric sequence).
➖ Arithmetic Sequences
An arithmetic sequence is a sequence of numbers in which the difference between any two consecutive terms is constant. This constant difference is called the common difference. For example, if the first term of an arithmetic sequence is a, and the common difference is d, the sequence can be represented as a, a + d, a + 2d, a + 3d, ... , where the nth term is given by a + (n-1)d. ➕
Because the difference between any two consecutive terms is the same, the terms in an arithmetic sequence have a constant rate of change. The rate of change is the common difference, d. Therefore, we can say that an arithmetic sequence is a function where the input variable is the term number, and the output variable is the value of the term, and the rate of change is constant. 🚙
For example, an arithmetic sequence with a first term of 5 and a common difference of 3 will look like this: 5, 8, 11, 14, 17, 20, ... . The rate of change between the terms is 3 and it is consistent throughout the sequence! Phew…
It's important to note that arithmetic sequences can be negative or positive, if the common difference is negative, it means the terms are decreasing and if the common difference is positive, it means the terms are increasing. ↕️

Source: Online Math Learning
😎 Formula and Example
The nth term of an arithmetic sequence with a common difference d is denoted by a_n, and it is given by the formula a_n = a_0 + dn, where a_0 is the initial value of the sequence. This formula allows you to calculate the value of any term in the sequence, given the value of the first term, a_0, and the common difference, d. The n in the formula represents the term number, so you can substitute any whole number in place of n to find the value of the corresponding term. 😌
Another way to represent the nth term of an arithmetic sequence is a = a_k + d(n-k), where a_k is the kth term of the sequence. This equation makes it possible to find the nth term of a sequence relative to a known term k. If you know the value of the kth term of the sequence and the common difference, you can use this formula to find the value of any other term.
For example, consider an arithmetic sequence with a first term of 5 and a common difference of 3. Using the first formula, the 5th term of the sequence can be calculated as a_5 = a_0 + dn = 5 + 3(5) = 20. Using the second formula, the 5th term of the sequence can also be calculated as a_5 = a_3 + d(5-2) = 11 + 3(3) = 20.
🔺 Geometric Sequences
A geometric sequence is a sequence of numbers in which the ratio of any two consecutive terms is constant. This constant ratio is called the common ratio. The common ratio can be represented as a fraction or decimal number. For example, if the first term of a geometric sequence is a, and the common ratio is r, the sequence can be represented as a, ar, ar^2, ar^3, ..., where the nth term is given by a*r^(n-1). ✖️
Because the ratio between any two consecutive terms is the same, the terms in a geometric sequence have a constant proportional change. The proportional change is the common ratio, r. Therefore, we can say that a geometric sequence is a function where the input variable is the term number, and the output variable is the value of the term, and the proportional change is constant.
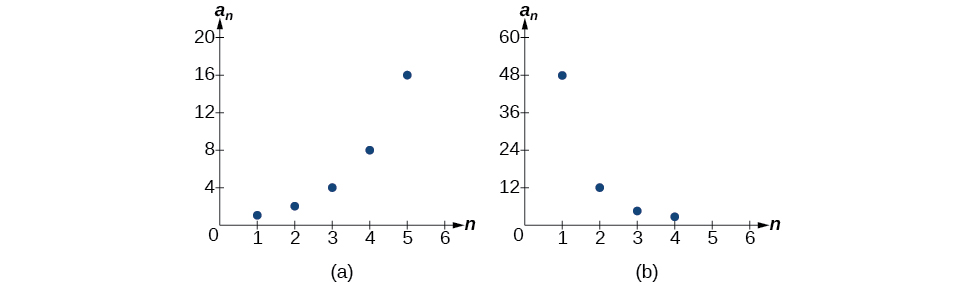
Source: Lumen Learning
For example, a geometric sequence with a first term of 2 and a common ratio of 3 will look like this: 2, 6, 18, 54, 162, ... . The proportional change between the terms is 3 and it is consistent throughout the sequence.
It's important to note that geometric sequences can be positive or negative, if the common ratio is between 0 and 1, it means the terms are decreasing and if the common ratio is greater than 1, it means the terms are increasing. ↕️
🤓 Formula
The nth term of a geometric sequence with a common ratio r is denoted by g_n, and it is given by the formula g_n = g_0 * r^n, where g_0 is the initial value of the sequence. This formula allows you to calculate the value of any term in the sequence, given the value of the first term, g_0, and the common ratio, r. The n in the formula represents the term number, so you can substitute any whole number in place of n to find the value of the corresponding term.

Source: Calcworkshop
Another way to represent the nth term of a geometric sequence is g_n = g_k * (r^(n-k)), where g_k is the kth term of the sequence. This equation makes it possible to find the nth term of a sequence relative to a known term k. If you know the value of the kth term of the sequence and the common ratio, you can use this formula to find the value of any other term.
It's important to note that while both formulas are equivalent and provide the same value for the nth term of a geometric sequence, the second one allows you to express the nth term in terms of a known term k, instead of the first term, which can be useful in certain situations.
🤔 Change vs. Rate of Change
When it comes to the rate of increase, arithmetic sequences have a constant increase with each step. This means that each term in the sequence increases by a fixed amount, which is the common difference. For example, an arithmetic sequence with a first term of 5 and a common difference of 3 will have terms 5, 8, 11, 14, 17, 20, ..., each term increases by 3. 🏎️
On the other hand, geometric sequences have an increasing rate of increase with each step. This means that each term in the sequence increases by a larger amount than the previous term. This is because each term is multiplied by the common ratio, which is greater than 1. For example, a geometric sequence with a first term of 2 and a common ratio of 3 will have terms 2, 6, 18, 54, 162, ..., each term increases by a factor of 3.
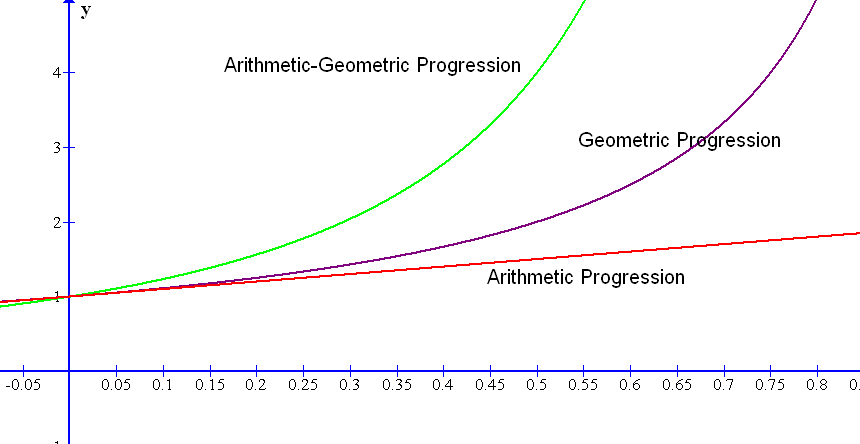
Source: Trans4mind
<< Hide Menu
2.1 Change in Arithmetic and Geometric Sequences
1 min read•june 18, 2024
2.1 Change in Arithmetic and Geometric Sequences
A sequence is a function from the whole numbers to the real numbers. This means that, a sequence takes a whole number (say, "n") and assigns it a real number. For example, think of a sequence of your class schedule, Monday is the first day, Tuesday the second, and so on. Each day of the week is assigned a number, Monday is 1, Tuesday is 2, and so on. 💯
Consequently, the graph of a sequence consists of discrete points instead of a curve. This is because in a sequence, we are only dealing with whole numbers, not with a continuous range of numbers like in a function. So, instead of having a smooth curve, we have a set of distinct points on a graph. 📌
For example, you might want to track the number of hours of sleep you get each night. You start on Monday and get 8 hours of sleep, on Tuesday you get 6 hours of sleep, on Wednesday you get 7 hours of sleep and so on. This is a sequence, where the input variable is the day of the week and the output variable is the number of hours of sleep. If we graph this, we would get a set of discrete points on a graph, one for each day of the week, instead of a smooth curve. 😴

Source: Desmos Graphing Calculator
Again, we’re looking at discrete points—don’t connect the dots like you’d typically do to draw a curve! Note that the sequence above is just a regular ol’ sequence (not an arithmetic or geometric sequence).
➖ Arithmetic Sequences
An arithmetic sequence is a sequence of numbers in which the difference between any two consecutive terms is constant. This constant difference is called the common difference. For example, if the first term of an arithmetic sequence is a, and the common difference is d, the sequence can be represented as a, a + d, a + 2d, a + 3d, ... , where the nth term is given by a + (n-1)d. ➕
Because the difference between any two consecutive terms is the same, the terms in an arithmetic sequence have a constant rate of change. The rate of change is the common difference, d. Therefore, we can say that an arithmetic sequence is a function where the input variable is the term number, and the output variable is the value of the term, and the rate of change is constant. 🚙
For example, an arithmetic sequence with a first term of 5 and a common difference of 3 will look like this: 5, 8, 11, 14, 17, 20, ... . The rate of change between the terms is 3 and it is consistent throughout the sequence! Phew…
It's important to note that arithmetic sequences can be negative or positive, if the common difference is negative, it means the terms are decreasing and if the common difference is positive, it means the terms are increasing. ↕️

Source: Online Math Learning
😎 Formula and Example
The nth term of an arithmetic sequence with a common difference d is denoted by a_n, and it is given by the formula a_n = a_0 + dn, where a_0 is the initial value of the sequence. This formula allows you to calculate the value of any term in the sequence, given the value of the first term, a_0, and the common difference, d. The n in the formula represents the term number, so you can substitute any whole number in place of n to find the value of the corresponding term. 😌
Another way to represent the nth term of an arithmetic sequence is a = a_k + d(n-k), where a_k is the kth term of the sequence. This equation makes it possible to find the nth term of a sequence relative to a known term k. If you know the value of the kth term of the sequence and the common difference, you can use this formula to find the value of any other term.
For example, consider an arithmetic sequence with a first term of 5 and a common difference of 3. Using the first formula, the 5th term of the sequence can be calculated as a_5 = a_0 + dn = 5 + 3(5) = 20. Using the second formula, the 5th term of the sequence can also be calculated as a_5 = a_3 + d(5-2) = 11 + 3(3) = 20.
🔺 Geometric Sequences
A geometric sequence is a sequence of numbers in which the ratio of any two consecutive terms is constant. This constant ratio is called the common ratio. The common ratio can be represented as a fraction or decimal number. For example, if the first term of a geometric sequence is a, and the common ratio is r, the sequence can be represented as a, ar, ar^2, ar^3, ..., where the nth term is given by a*r^(n-1). ✖️
Because the ratio between any two consecutive terms is the same, the terms in a geometric sequence have a constant proportional change. The proportional change is the common ratio, r. Therefore, we can say that a geometric sequence is a function where the input variable is the term number, and the output variable is the value of the term, and the proportional change is constant.

Source: Lumen Learning
For example, a geometric sequence with a first term of 2 and a common ratio of 3 will look like this: 2, 6, 18, 54, 162, ... . The proportional change between the terms is 3 and it is consistent throughout the sequence.
It's important to note that geometric sequences can be positive or negative, if the common ratio is between 0 and 1, it means the terms are decreasing and if the common ratio is greater than 1, it means the terms are increasing. ↕️
🤓 Formula
The nth term of a geometric sequence with a common ratio r is denoted by g_n, and it is given by the formula g_n = g_0 * r^n, where g_0 is the initial value of the sequence. This formula allows you to calculate the value of any term in the sequence, given the value of the first term, g_0, and the common ratio, r. The n in the formula represents the term number, so you can substitute any whole number in place of n to find the value of the corresponding term.

Source: Calcworkshop
Another way to represent the nth term of a geometric sequence is g_n = g_k * (r^(n-k)), where g_k is the kth term of the sequence. This equation makes it possible to find the nth term of a sequence relative to a known term k. If you know the value of the kth term of the sequence and the common ratio, you can use this formula to find the value of any other term.
It's important to note that while both formulas are equivalent and provide the same value for the nth term of a geometric sequence, the second one allows you to express the nth term in terms of a known term k, instead of the first term, which can be useful in certain situations.
🤔 Change vs. Rate of Change
When it comes to the rate of increase, arithmetic sequences have a constant increase with each step. This means that each term in the sequence increases by a fixed amount, which is the common difference. For example, an arithmetic sequence with a first term of 5 and a common difference of 3 will have terms 5, 8, 11, 14, 17, 20, ..., each term increases by 3. 🏎️
On the other hand, geometric sequences have an increasing rate of increase with each step. This means that each term in the sequence increases by a larger amount than the previous term. This is because each term is multiplied by the common ratio, which is greater than 1. For example, a geometric sequence with a first term of 2 and a common ratio of 3 will have terms 2, 6, 18, 54, 162, ..., each term increases by a factor of 3.

Source: Trans4mind

© 2024 Fiveable Inc. All rights reserved.