Browse By Unit
2.5 Exponential Function Context and Data Modeling
1 min read•june 18, 2024
2.5 Exponential Function Context and Data Modeling
Exponential functions model growth patterns where successive output values over equal-length input-value intervals are proportional. 📈
As a reminder, the general form of an exponential function is , where a is the initial value and b is the base, a positive number other than 1. The base, b, represents the constant proportion by which the output value is multiplied at each step.
When the base is greater than 1, the function demonstrates exponential growth, meaning that the output values increase at an increasing rate. When the base is between 0 and 1, the function demonstrates exponential decay, meaning that the output values decrease at a decreasing rate.
When the input values are whole numbers, exponential functions model situations of repeated multiplication of a constant to an initial value.
🤨 What if we add a constant?
In some cases, a data set may not immediately reveal an exponential growth pattern, even though the relationship between the independent and dependent variables is actually exponential. One reason for this is that the initial value of the dependent variable may not be zero. In such cases, a constant may need to be added to the dependent variable values of a data set to reveal a proportional growth pattern.
For example, let's say we have a data set that represents the population of a certain city over time. The data set may not show an exponential growth pattern because the population has always been greater than zero. 🧍
If we want to analyze the population growth rate, we need to consider the population growth rate as a proportion of the initial population. To do this, we can add a constant, say k, to the population values, so the new dependent variable would be . Now we can analyze the growth rate of y' over time, which will be proportional.
Another example could be an investment that starts at a certain value and the growth rate is not immediately visible until we add a constant to the value of the investment.
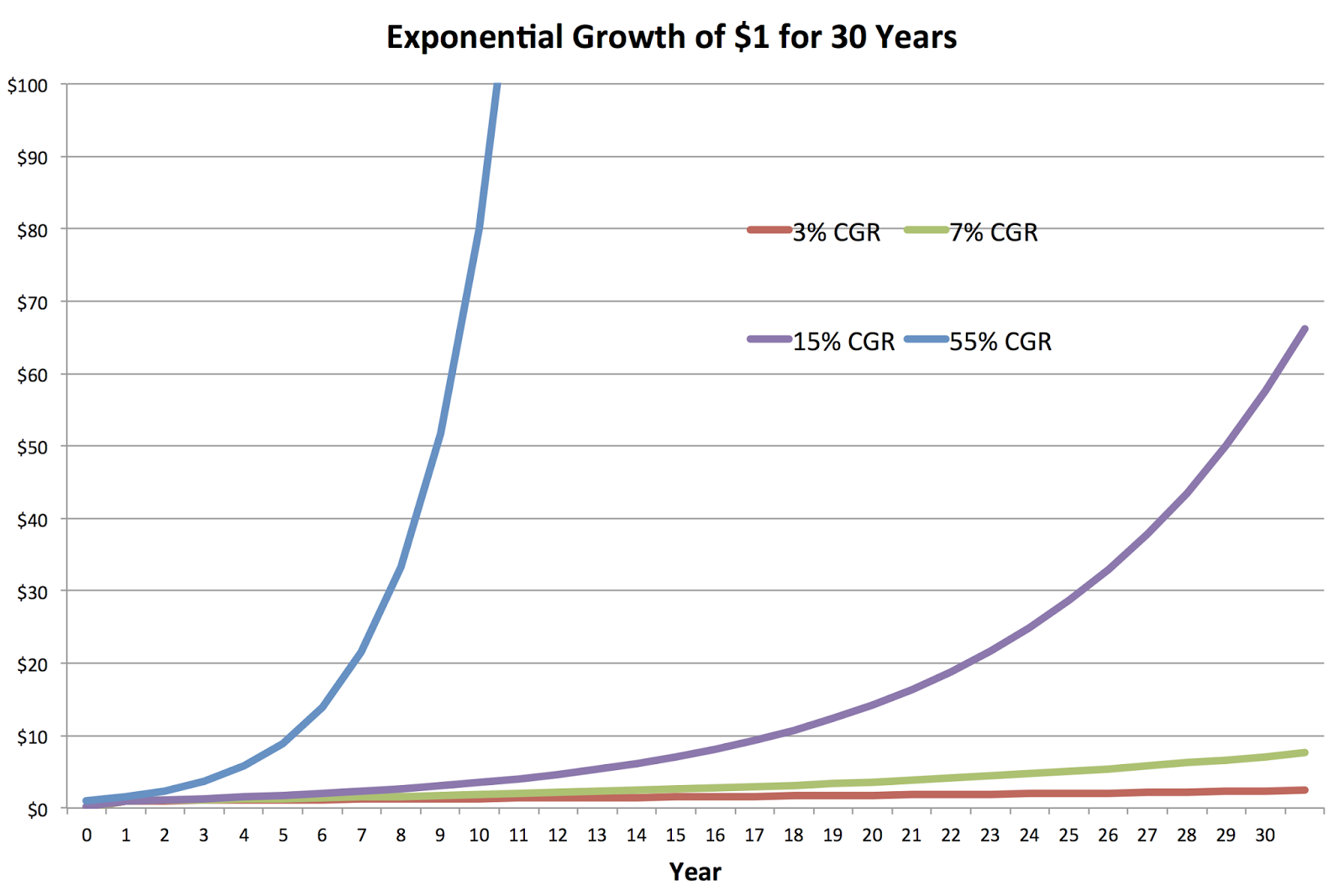
Source: Seeking Alpha
This idea is important in precalculus because it allows us to analyze and understand the growth patterns of real-world data sets, even when the data doesn't reveal the pattern immediately. This can be done by performing mathematical operations on the data set, such as adding a constant, to reveal the underlying exponential growth pattern. 🤓
👀 Looking at Intro-Output Pairs and Technology
An exponential function can also be constructed using two input-output pairs. For example, if we know the values of two input-output pairs (x1, y1) and (x2, y2), we can use these values to find the initial value (a) and the base (b) of the exponential function.
We can set up a system of equations using the two input-output pairs and solve it to find the values of the initial value and the base.
For example, if we have two input-output pairs (x1, y1) = (0, a) and (x2, y2) = (1, ab), we can set up the following system of equations: |
Solving this system of equations we get: |
This process can be used to construct an exponential function model from any two input-output pairs! 👏
Exponential function models can be constructed for a data set with the use of technology, specifically through exponential regression. Exponential regression is a method used to fit an exponential function to a set of data points. This method can be used to find the best-fit exponential function that models the data.
There are different ways to perform exponential regression, but generally, it involves using a software or calculator that can perform non-linear regression. This software or calculator will take the data set as input and will output the best-fit exponential function. The best-fit function is the function that minimizes the difference between the observed data points and the function's predicted values. 👔
The output of the exponential regression will typically include the values of the initial value (a) and the base (b) of the exponential function, as well as other statistics such as the correlation coefficient (R^2), which measures how well the model fits the data, and the residuals, which measure the difference between the observed data and the predicted values.
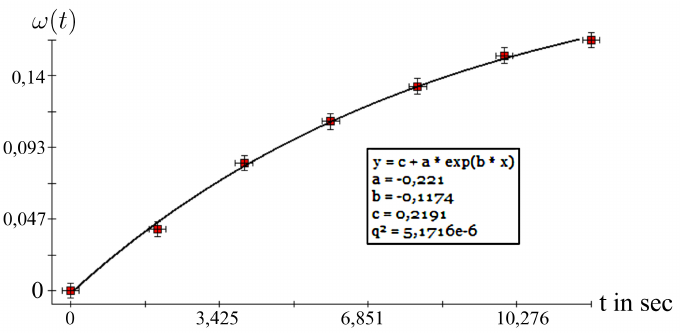
Source: ResearchGate
👋🏾 Meet the New Kid on the Block: e!
The natural base e, which is approximately 2.718, is often used as the base in exponential functions that model contextual scenarios. The number e is a mathematical constant that has many important properties and applications in mathematics and science. 🥼
One of the main reasons why e is used as the base in exponential functions is that it has a special relationship with the concept of continuous growth. For example, the function models the continuous growth of an investment that earns a constant interest rate of 100%. The function models the continuous decay of a substance that decays at a constant rate.
Another reason why e is used as the base in exponential functions is that it is the base of the natural logarithm, denoted by ln. The natural logarithm is the inverse function of the exponential function with base e. This means that if we take the natural logarithm of an exponential function with base e, we get the original input value. This property makes it easy to solve equations involving exponential functions with base e. 🎈
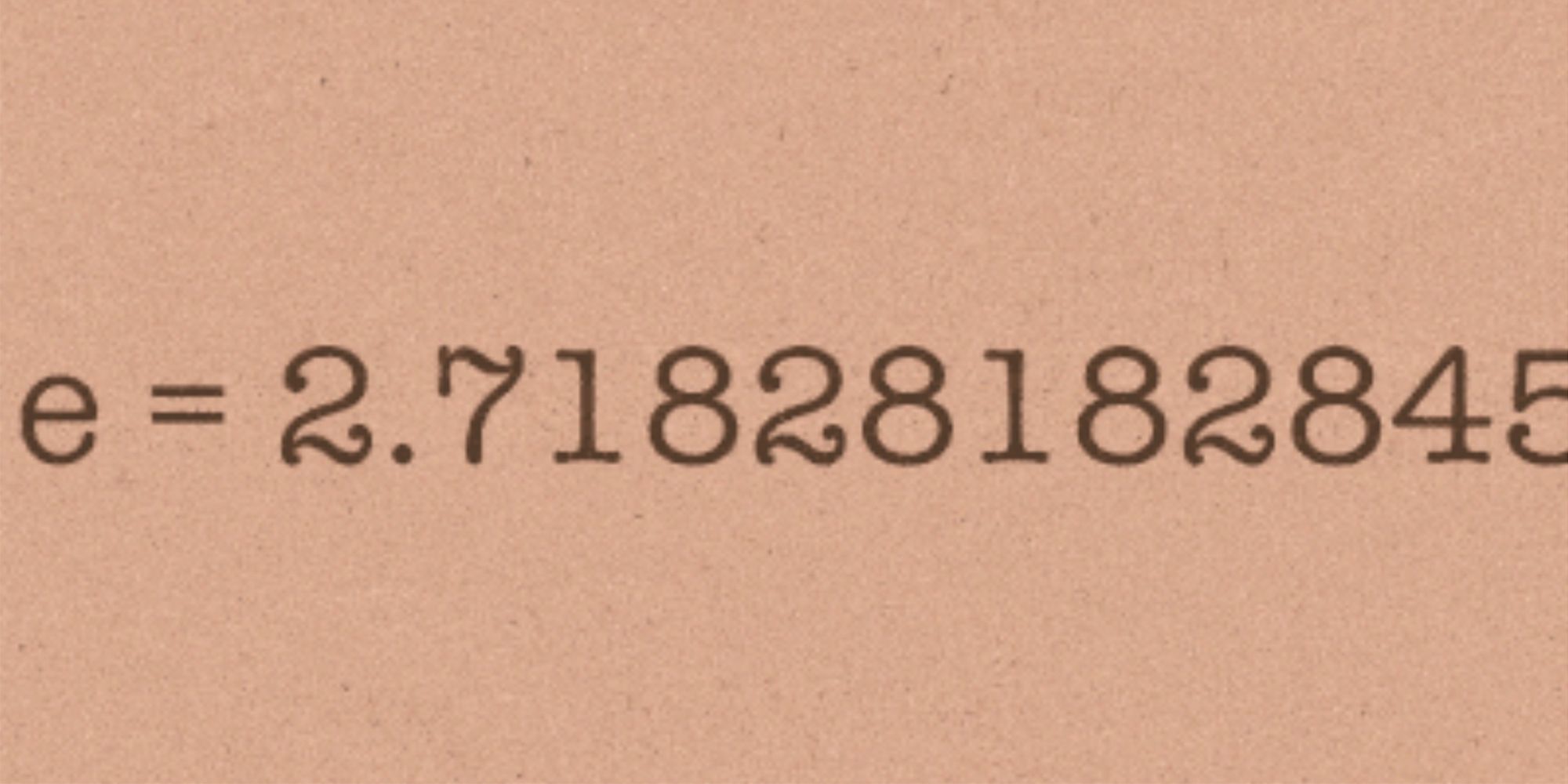
Source: Popular Mechanics
⚖️ Equivalent Forms
Equivalent forms of an exponential function can reveal different properties of the function. Equivalent forms of an exponential function have the same graph and the same behavior over time, but they can have different interpretations of the growth rate. 🏋️♀️
For example, consider the function , where d represents the number of days. The base of this function indicates that the quantity increases by a factor of 2 every day. This means that if we start with 1 unit of the quantity, after 1 day, we will have 2 units, after 2 days, we will have 4 units, and so on.
Now consider the equivalent form of the function, , where d represents the number of days. The base of this function indicates that the quantity increases by a factor of every week. This means that if we start with 1 unit of the quantity, after 1 week, we will have 128 units, after 2 weeks, we will have 16,384 units, and so on.
In the first function, the base of 2 indicates that the quantity doubles every day. In the second function, the base of indicates that the quantity multiplies by 128 every week. Both functions have the same behavior over time, but the interpretation of the growth rate is different.
<< Hide Menu
2.5 Exponential Function Context and Data Modeling
1 min read•june 18, 2024
2.5 Exponential Function Context and Data Modeling
Exponential functions model growth patterns where successive output values over equal-length input-value intervals are proportional. 📈
As a reminder, the general form of an exponential function is , where a is the initial value and b is the base, a positive number other than 1. The base, b, represents the constant proportion by which the output value is multiplied at each step.
When the base is greater than 1, the function demonstrates exponential growth, meaning that the output values increase at an increasing rate. When the base is between 0 and 1, the function demonstrates exponential decay, meaning that the output values decrease at a decreasing rate.
When the input values are whole numbers, exponential functions model situations of repeated multiplication of a constant to an initial value.
🤨 What if we add a constant?
In some cases, a data set may not immediately reveal an exponential growth pattern, even though the relationship between the independent and dependent variables is actually exponential. One reason for this is that the initial value of the dependent variable may not be zero. In such cases, a constant may need to be added to the dependent variable values of a data set to reveal a proportional growth pattern.
For example, let's say we have a data set that represents the population of a certain city over time. The data set may not show an exponential growth pattern because the population has always been greater than zero. 🧍
If we want to analyze the population growth rate, we need to consider the population growth rate as a proportion of the initial population. To do this, we can add a constant, say k, to the population values, so the new dependent variable would be . Now we can analyze the growth rate of y' over time, which will be proportional.
Another example could be an investment that starts at a certain value and the growth rate is not immediately visible until we add a constant to the value of the investment.

Source: Seeking Alpha
This idea is important in precalculus because it allows us to analyze and understand the growth patterns of real-world data sets, even when the data doesn't reveal the pattern immediately. This can be done by performing mathematical operations on the data set, such as adding a constant, to reveal the underlying exponential growth pattern. 🤓
👀 Looking at Intro-Output Pairs and Technology
An exponential function can also be constructed using two input-output pairs. For example, if we know the values of two input-output pairs (x1, y1) and (x2, y2), we can use these values to find the initial value (a) and the base (b) of the exponential function.
We can set up a system of equations using the two input-output pairs and solve it to find the values of the initial value and the base.
For example, if we have two input-output pairs (x1, y1) = (0, a) and (x2, y2) = (1, ab), we can set up the following system of equations: |
Solving this system of equations we get: |
This process can be used to construct an exponential function model from any two input-output pairs! 👏
Exponential function models can be constructed for a data set with the use of technology, specifically through exponential regression. Exponential regression is a method used to fit an exponential function to a set of data points. This method can be used to find the best-fit exponential function that models the data.
There are different ways to perform exponential regression, but generally, it involves using a software or calculator that can perform non-linear regression. This software or calculator will take the data set as input and will output the best-fit exponential function. The best-fit function is the function that minimizes the difference between the observed data points and the function's predicted values. 👔
The output of the exponential regression will typically include the values of the initial value (a) and the base (b) of the exponential function, as well as other statistics such as the correlation coefficient (R^2), which measures how well the model fits the data, and the residuals, which measure the difference between the observed data and the predicted values.

Source: ResearchGate
👋🏾 Meet the New Kid on the Block: e!
The natural base e, which is approximately 2.718, is often used as the base in exponential functions that model contextual scenarios. The number e is a mathematical constant that has many important properties and applications in mathematics and science. 🥼
One of the main reasons why e is used as the base in exponential functions is that it has a special relationship with the concept of continuous growth. For example, the function models the continuous growth of an investment that earns a constant interest rate of 100%. The function models the continuous decay of a substance that decays at a constant rate.
Another reason why e is used as the base in exponential functions is that it is the base of the natural logarithm, denoted by ln. The natural logarithm is the inverse function of the exponential function with base e. This means that if we take the natural logarithm of an exponential function with base e, we get the original input value. This property makes it easy to solve equations involving exponential functions with base e. 🎈
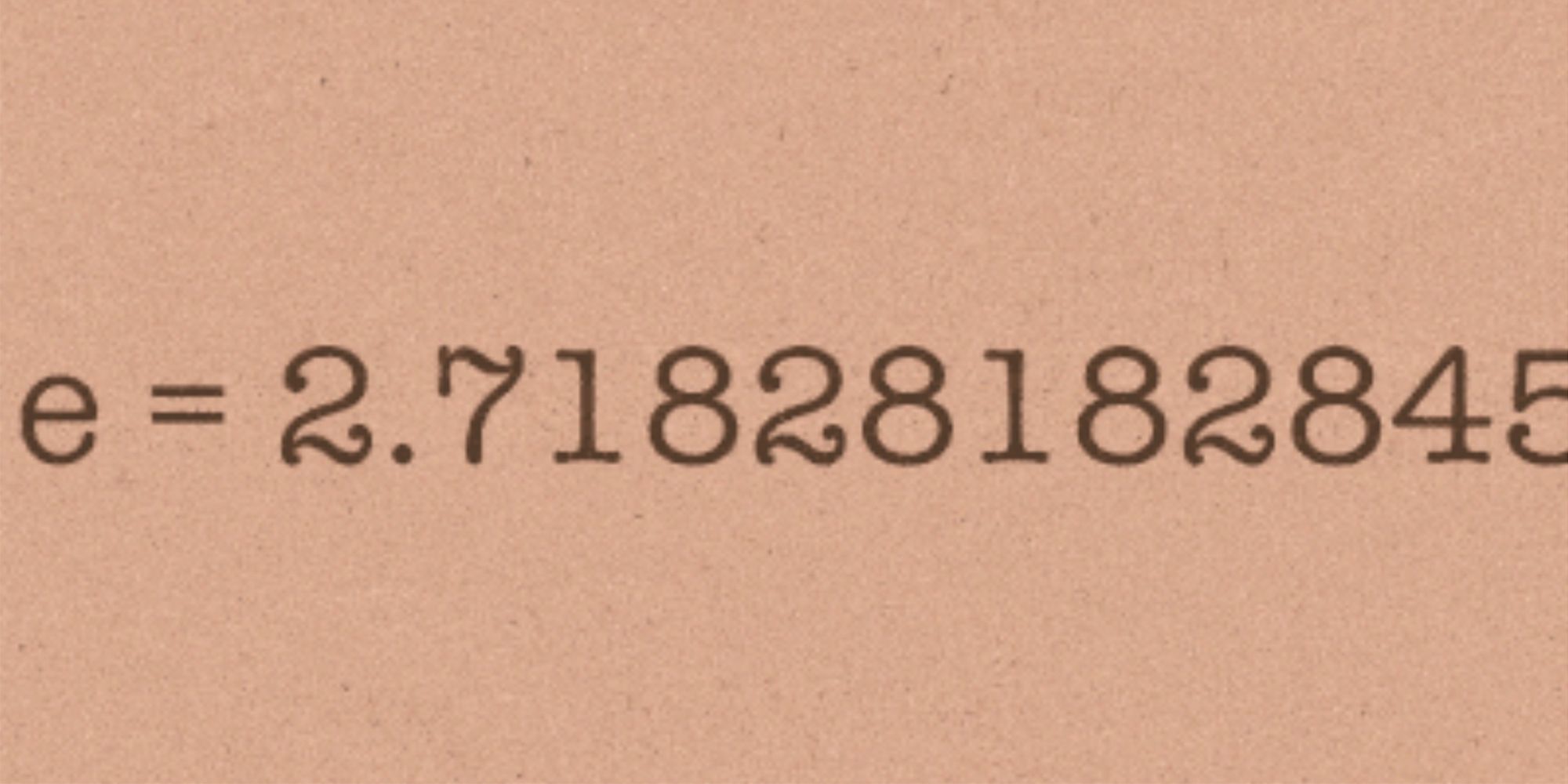
Source: Popular Mechanics
⚖️ Equivalent Forms
Equivalent forms of an exponential function can reveal different properties of the function. Equivalent forms of an exponential function have the same graph and the same behavior over time, but they can have different interpretations of the growth rate. 🏋️♀️
For example, consider the function , where d represents the number of days. The base of this function indicates that the quantity increases by a factor of 2 every day. This means that if we start with 1 unit of the quantity, after 1 day, we will have 2 units, after 2 days, we will have 4 units, and so on.
Now consider the equivalent form of the function, , where d represents the number of days. The base of this function indicates that the quantity increases by a factor of every week. This means that if we start with 1 unit of the quantity, after 1 week, we will have 128 units, after 2 weeks, we will have 16,384 units, and so on.
In the first function, the base of 2 indicates that the quantity doubles every day. In the second function, the base of indicates that the quantity multiplies by 128 every week. Both functions have the same behavior over time, but the interpretation of the growth rate is different.

© 2024 Fiveable Inc. All rights reserved.