Browse By Unit
2.4 Exponential Function Manipulation
1 min read•june 18, 2024
2.4 Exponential Function Manipulation
Fun fact: in precalculus, we can manipulate exponential functions in various ways to simplify them, to solve equations or to model real-world situations! Here, we’ll refer to each of them as a “property” to remember them more easily! 🎐
Properties of Exponential Functions
🙅🏾 Product Property
The product property for exponents states that for any base b, and exponents m and n, . This property is a direct consequence of the distributive property of multiplication over addition. The product property for exponents can be used to simplify expressions that involve multiple exponents with the same base. 🎪
Graphically, this property implies that every horizontal translation of an exponential function, (first image), is equivalent to a vertical dilation (second image), where This means that when we shift the graph of the exponential function units to the right, the graph of the function will be the same as the graph of the function .

An example of the product property being using on the function f(x)=b^(x+k). The final function is f(x)= ab^x.
Source: Jed Q
For example, if we have a graph of and we shift the graph k units to the right, the graph of the function will be the same as the graph of the function !
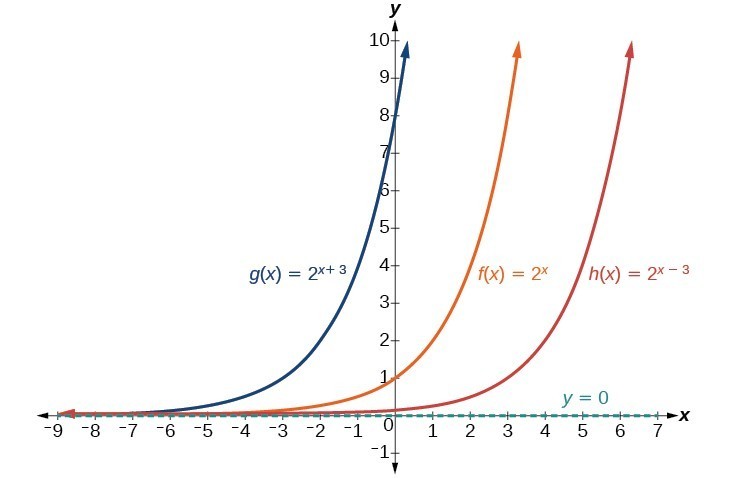
Source: Lumen Learning
This property can be used to simplify the analysis of exponential functions. For example, if we have a graph of , we can observe the behavior of the function for x > 0, and by using the property we can also observe the behavior for x < 0.
🔋 Power Property
The power property for exponents states that for any base b, and exponents m and n, . This property is a direct consequence of the distributive property of exponentiation over multiplication. The power property for exponents can be used to simplify expressions that involve multiple exponents with the same base. 🔌
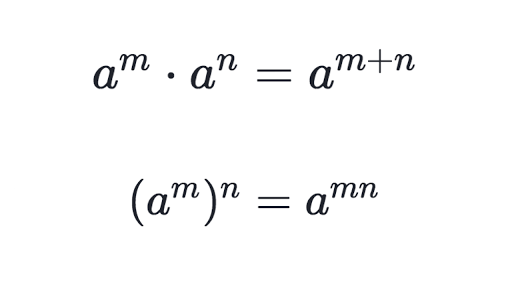
Source: Khan Academy
Graphically, this property implies that every horizontal dilation of an exponential function, f(x) = b^(cx), is equivalent to a change of the base of an exponential function, , where is a constant and c ≠ 0. This means that when we stretch the graph of the exponential function by a factor of c, the graph of the function will be the same as the graph of the function .
For example, if we have a graph of and we stretch it by a factor of 3, the graph of the function will be the same as the graph of the function
➖ Negative Exponent Property
The negative exponent property states that for any base b and exponent n, . This property can be used to simplify expressions that involve negative exponents. ☹️
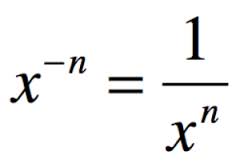
Source:
Graphically, this property implies that every reflection of the exponential function over the y-axis, is equivalent to a function . This means that when we reflect the graph of the exponential function over the y-axis, the graph of the function will be the same as the graph of the function .
For example, if we have a graph of and we reflect it over the y-axis, the graph of the function will be the same as the graph of the function

Source: Math LibreTexts
This property can be used to simplify the analysis of exponential functions. For example, if we have a graph of and we reflect it over the y-axis we can see that the graph is the same as the graph of ) and we can analyze the behavior of the function with a different exponent.
It's important to note that this property is true for any base, not only for base 2. Additionally, it's important to remember that this property is valid only for positive bases, when the base is negative the property doesn't hold.
Value of Exponential Functions
An exponential unit fraction, such as b^(1/k) where k is a natural number, is a value that represents the kth root of b. 🍕
The value of an exponential expression involving an exponential unit fraction is the kth root of b, when it exists.
For example, the value of 2^(1/3) is the cube root of 2, which is approximately 1.259921. In this case, the cube root of 2 exists, and it is represented by the exponential unit fraction 2^(1/3).
In general, for positive real numbers b, the kth root of b exists if k is a natural number and the kth root of b is a real number. For example, the square root of a positive real number b exists and is represented by the exponential unit fraction b^(1/2), the cube root of b exists and is represented by the exponential unit fraction b^(1/3), and so on.
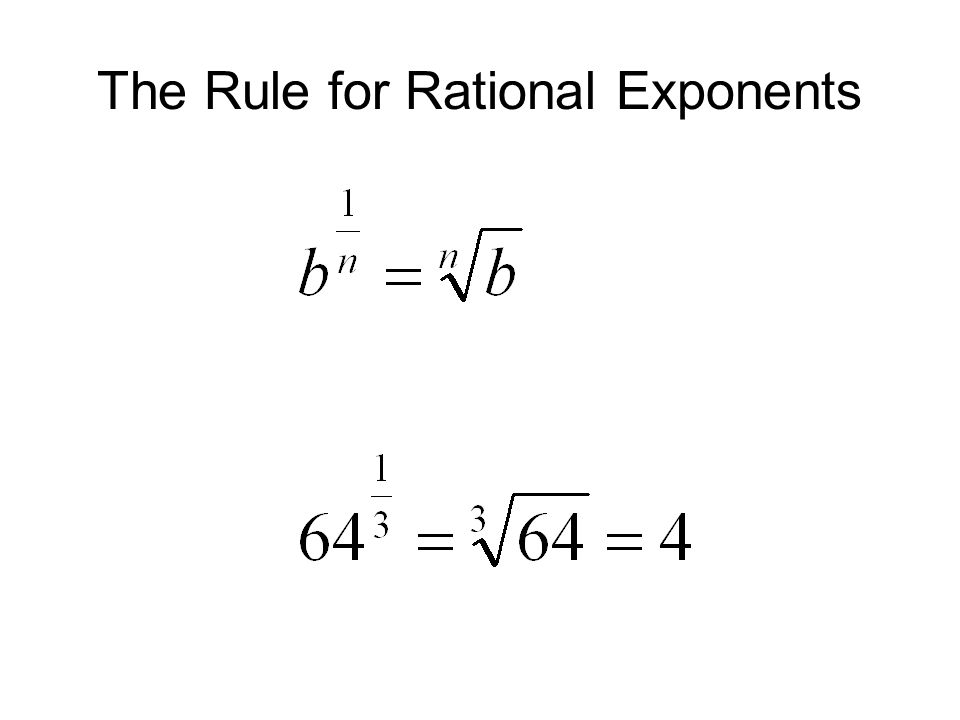
Source: Quizlet
On the other hand, if the base is a negative real number and the exponent is a rational number (1/k) then the value of the expression doesn't exist in the real numbers, but it exists in the complex numbers. ❓
<< Hide Menu
2.4 Exponential Function Manipulation
1 min read•june 18, 2024
2.4 Exponential Function Manipulation
Fun fact: in precalculus, we can manipulate exponential functions in various ways to simplify them, to solve equations or to model real-world situations! Here, we’ll refer to each of them as a “property” to remember them more easily! 🎐
Properties of Exponential Functions
🙅🏾 Product Property
The product property for exponents states that for any base b, and exponents m and n, . This property is a direct consequence of the distributive property of multiplication over addition. The product property for exponents can be used to simplify expressions that involve multiple exponents with the same base. 🎪
Graphically, this property implies that every horizontal translation of an exponential function, (first image), is equivalent to a vertical dilation (second image), where This means that when we shift the graph of the exponential function units to the right, the graph of the function will be the same as the graph of the function .

An example of the product property being using on the function f(x)=b^(x+k). The final function is f(x)= ab^x.
Source: Jed Q
For example, if we have a graph of and we shift the graph k units to the right, the graph of the function will be the same as the graph of the function !

Source: Lumen Learning
This property can be used to simplify the analysis of exponential functions. For example, if we have a graph of , we can observe the behavior of the function for x > 0, and by using the property we can also observe the behavior for x < 0.
🔋 Power Property
The power property for exponents states that for any base b, and exponents m and n, . This property is a direct consequence of the distributive property of exponentiation over multiplication. The power property for exponents can be used to simplify expressions that involve multiple exponents with the same base. 🔌
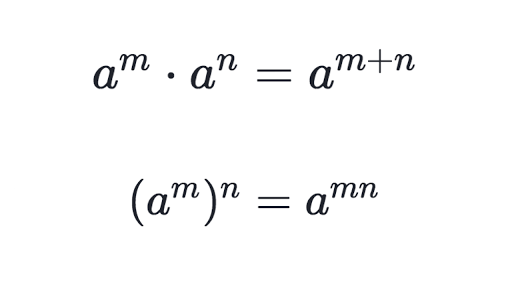
Source: Khan Academy
Graphically, this property implies that every horizontal dilation of an exponential function, f(x) = b^(cx), is equivalent to a change of the base of an exponential function, , where is a constant and c ≠ 0. This means that when we stretch the graph of the exponential function by a factor of c, the graph of the function will be the same as the graph of the function .
For example, if we have a graph of and we stretch it by a factor of 3, the graph of the function will be the same as the graph of the function
➖ Negative Exponent Property
The negative exponent property states that for any base b and exponent n, . This property can be used to simplify expressions that involve negative exponents. ☹️
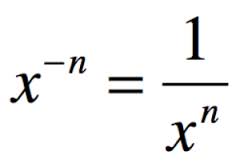
Source:
Graphically, this property implies that every reflection of the exponential function over the y-axis, is equivalent to a function . This means that when we reflect the graph of the exponential function over the y-axis, the graph of the function will be the same as the graph of the function .
For example, if we have a graph of and we reflect it over the y-axis, the graph of the function will be the same as the graph of the function

Source: Math LibreTexts
This property can be used to simplify the analysis of exponential functions. For example, if we have a graph of and we reflect it over the y-axis we can see that the graph is the same as the graph of ) and we can analyze the behavior of the function with a different exponent.
It's important to note that this property is true for any base, not only for base 2. Additionally, it's important to remember that this property is valid only for positive bases, when the base is negative the property doesn't hold.
Value of Exponential Functions
An exponential unit fraction, such as b^(1/k) where k is a natural number, is a value that represents the kth root of b. 🍕
The value of an exponential expression involving an exponential unit fraction is the kth root of b, when it exists.
For example, the value of 2^(1/3) is the cube root of 2, which is approximately 1.259921. In this case, the cube root of 2 exists, and it is represented by the exponential unit fraction 2^(1/3).
In general, for positive real numbers b, the kth root of b exists if k is a natural number and the kth root of b is a real number. For example, the square root of a positive real number b exists and is represented by the exponential unit fraction b^(1/2), the cube root of b exists and is represented by the exponential unit fraction b^(1/3), and so on.
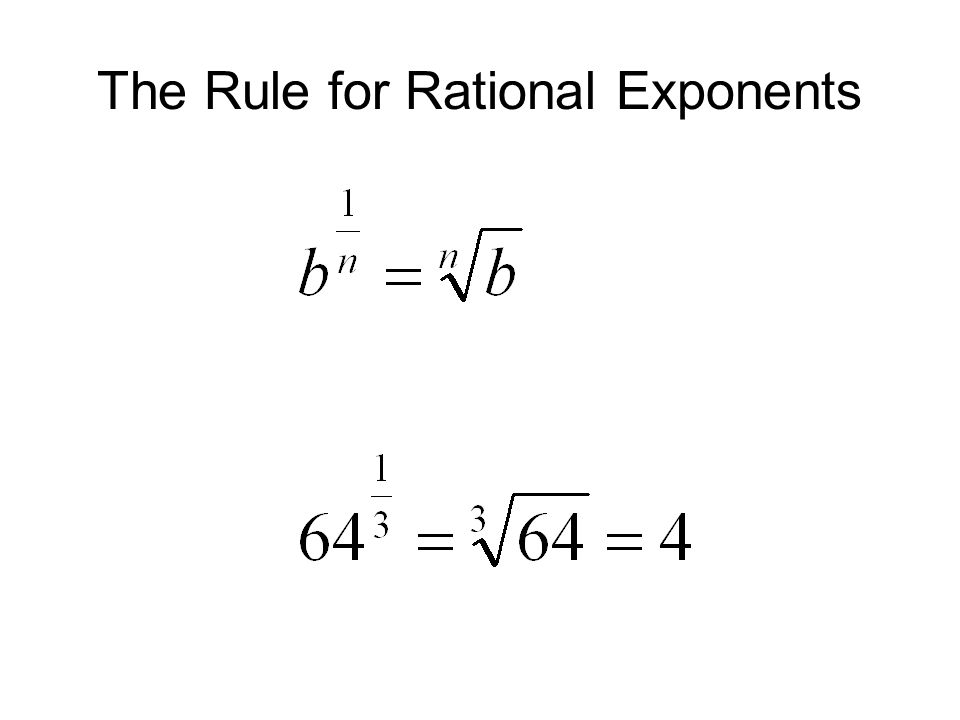
Source: Quizlet
On the other hand, if the base is a negative real number and the exponent is a rational number (1/k) then the value of the expression doesn't exist in the real numbers, but it exists in the complex numbers. ❓

© 2024 Fiveable Inc. All rights reserved.