Browse By Unit
2.9 Logarithmic Expressions
Not too long ago (aka in recent sections), we talked about exponential functions in the context of precalculus, modeling, and function manipulation. Ever wondered what happens when we tweak them a little bit? We get logarithmic expressions!
In more formal terms, the logarithmic expression log_b(c) (Sorry for the typing format! The b is a subscript in this case) is known as the “logarithm of c to the base b.” The logarithm of a number is defined as the exponent to which the base must be raised to produce that number. So in the equation log_b(c) = a, the base b is raised to the power of a to produce the number c. 😲

Source: Google Sites
Note that the base b must be a positive number, and cannot be equal to 1. This is because if b = 1, then b^a would always equal 1, and the logarithm would not have a unique value. ➕
The common logarithm is a logarithm with a base of 10, and is often denoted as log(c). The natural logarithm, denoted by ln(c) is a logarithm with base e (approx 2.71828) where e is the Euler's number. 🔟 Relating Logs and Exponents****
The logarithm is the inverse function (whoa!—remember 2.8?) of the exponential function. This means that if we have an exponential equation of the form b^x = c, we can find x by taking the logarithm of both sides with base b. This will give us x = log_b(c).
Some logarithmic expressions can be easily calculated by hand using basic arithmetic, while others may be more difficult or impossible to calculate without the use of technology. 😵💫
For example, log_2(64) can be easily computed by hand as log_2(2^6) = 6, while log_2(1000000) may be more difficult to calculate and would likely require the use of a calculator or computer! 💻
Logarithmic Scales
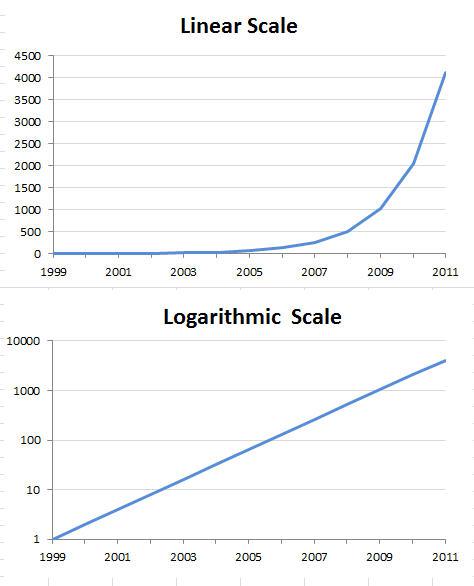
A logarithmic scale is a way of representing a range of values over a wide range of magnitudes in a compact way. 🎚️
How is this different from the standard linear scale we’re used to since Algebra/Integrated Math I? 🤔
- In a standard linear scale, the units of measure are equally spaced and each unit represents a fixed increment of the value being measured. ⚖️
- In a logarithmic scale, the units represent a multiplicative change of the base of the logarithm. ✖️
Source: Forbes
For example, on a standard linear scale using base 10, the units might be 0,1,2,3,4,5,…, while on a logarithmic scale using base 10, the units might be 10^0, 10^1, 10^2, 10^3, 10^4, 10^5,… This means that on a logarithmic scale, each unit represents a power of 10. 👊
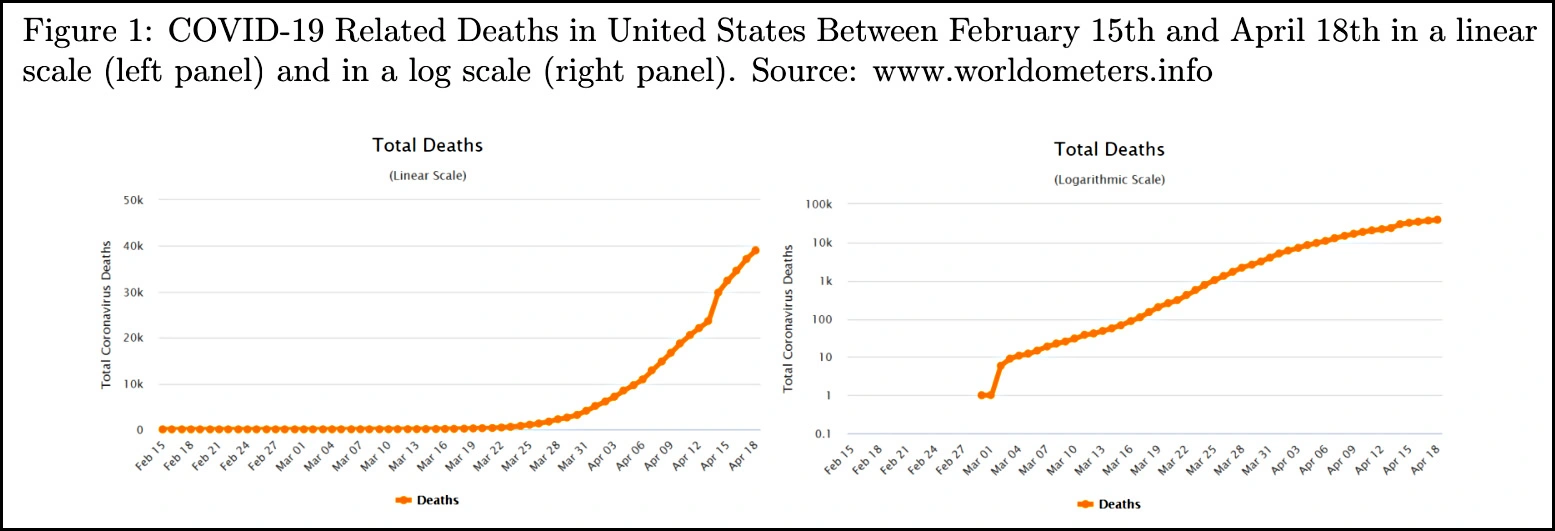
This property of logarithmic scales makes them useful in displaying data that spans several orders of magnitude, such as in fields like astronomy, engineering, medicine, and finance. ✨
Source: Mother Jones
Awesome! In the next couple sections, we’ll look at deeper connections between logs and exponents and explore logarithmic functions! 💯
<< Hide Menu
2.9 Logarithmic Expressions
Not too long ago (aka in recent sections), we talked about exponential functions in the context of precalculus, modeling, and function manipulation. Ever wondered what happens when we tweak them a little bit? We get logarithmic expressions!
In more formal terms, the logarithmic expression log_b(c) (Sorry for the typing format! The b is a subscript in this case) is known as the “logarithm of c to the base b.” The logarithm of a number is defined as the exponent to which the base must be raised to produce that number. So in the equation log_b(c) = a, the base b is raised to the power of a to produce the number c. 😲

Source: Google Sites
Note that the base b must be a positive number, and cannot be equal to 1. This is because if b = 1, then b^a would always equal 1, and the logarithm would not have a unique value. ➕
The common logarithm is a logarithm with a base of 10, and is often denoted as log(c). The natural logarithm, denoted by ln(c) is a logarithm with base e (approx 2.71828) where e is the Euler's number. 🔟 Relating Logs and Exponents****
The logarithm is the inverse function (whoa!—remember 2.8?) of the exponential function. This means that if we have an exponential equation of the form b^x = c, we can find x by taking the logarithm of both sides with base b. This will give us x = log_b(c).
Some logarithmic expressions can be easily calculated by hand using basic arithmetic, while others may be more difficult or impossible to calculate without the use of technology. 😵💫
For example, log_2(64) can be easily computed by hand as log_2(2^6) = 6, while log_2(1000000) may be more difficult to calculate and would likely require the use of a calculator or computer! 💻
Logarithmic Scales
A logarithmic scale is a way of representing a range of values over a wide range of magnitudes in a compact way. 🎚️
How is this different from the standard linear scale we’re used to since Algebra/Integrated Math I? 🤔
- In a standard linear scale, the units of measure are equally spaced and each unit represents a fixed increment of the value being measured. ⚖️
- In a logarithmic scale, the units represent a multiplicative change of the base of the logarithm. ✖️

Source: Forbes
For example, on a standard linear scale using base 10, the units might be 0,1,2,3,4,5,…, while on a logarithmic scale using base 10, the units might be 10^0, 10^1, 10^2, 10^3, 10^4, 10^5,… This means that on a logarithmic scale, each unit represents a power of 10. 👊
This property of logarithmic scales makes them useful in displaying data that spans several orders of magnitude, such as in fields like astronomy, engineering, medicine, and finance. ✨

Source: Mother Jones
Awesome! In the next couple sections, we’ll look at deeper connections between logs and exponents and explore logarithmic functions! 💯

© 2024 Fiveable Inc. All rights reserved.