Browse By Unit
Jesse
Jesse
3.1 Periodic Phenomena
Have you hopped on a carousel ride before? 🎠
If so, have you even wondered why you come back to the starting point whenever you complete an entire revolution again, again, and again when you were younger?

Source: Pacific Park
…Or maybe you were in a ferris wheel and you cycle from getting to the top to coming back to the bottom. 🎡
What do carousels and ferris wheels have in common? They’re both examples of periodic phenomena in real life! Now let’s translate this piece of information into the world of precalculus. 🏃
A periodic relationship is a type of mathematical relationship that can be observed between two aspects of a given context. These relationships can be identified by observing a repeating pattern in the output values as the input values increase over successive, equal length intervals. 🔄 The output values will repeat this pattern at regular intervals, hence the name "periodic relationship."
One way to visualize a periodic relationship is through the use of a graph. A graph is a visual representation of a mathematical relationship, and it can be used to illustrate the repeating pattern of a periodic relationship. By plotting the input and output values on a graph, the repeating pattern of the relationship can be clearly observed.
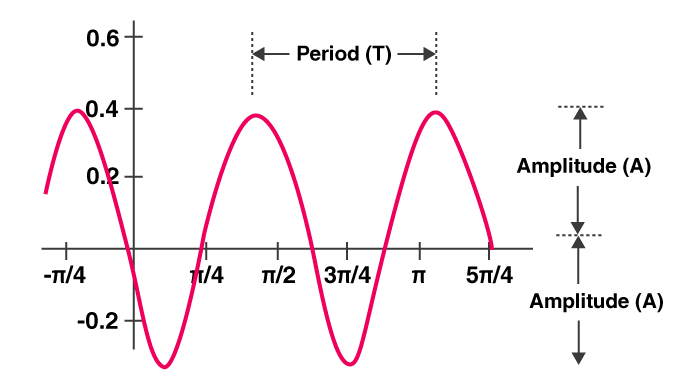
Source: Byjus
🔀 Periods = Cycles
It is important to note that the graph of a periodic relationship can be constructed from the graph of a single cycle of the relationship. This is because the repeating pattern of a periodic relationship is consistent across all cycles, meaning that the shape of the graph will be the same for each cycle. By analyzing the graph of a single cycle, one can understand the overall behavior of the periodic relationship. 🔘
The period of a function is a key concept in understanding periodic relationships. It is defined as the smallest positive value of k for which the function f(x + k) is equal to f(x) for all x in the domain of the function.
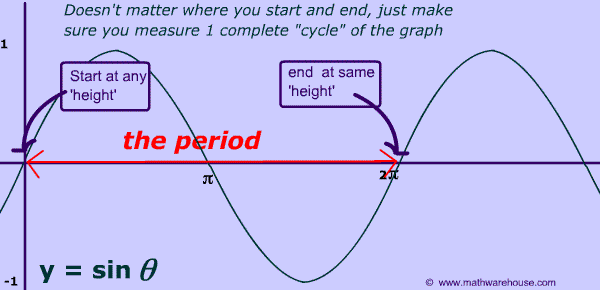
Source: Math Warehouse
One important property of a periodic function is that it can be completely determined by any interval of width k. This means that if we know the behavior of the function over a single interval of width k, we can deduce the behavior of the function over any other interval of the same width. This is because the function will repeat its behavior over these intervals with the same pattern.
For example, if we know the behavior of the function f(x) over the interval [0, k], we can deduce the behavior of the function over the interval [k, 2k] and so on. This is because the function will repeat its behavior over the interval [k, 2k] with the same pattern as it did over the interval [0,k].
It is also important to note that a function can have multiple periods. ♾️ For example, if a function has a period of 4, it also has a period of 8, 12, etc. But the smallest period is called the fundamental period (no need to remember for the AP exam).
In order to estimate the period of a function, one can investigate successive equal-length output values and look for patterns that repeat. Once a repeating pattern is found, the length of that pattern can be considered the period of the function! 📐
🌐 Other Properties: Concavities & Rates of Change
Periodic functions also have other characteristics, such as intervals of increase and decrease, different concavities, and various rates of change. However, unlike non-periodic functions, these characteristics will be consistent throughout all periods of the function. 🎓
For example, if a periodic function has an interval of increase in the first period, it will also have an interval of increase in every subsequent period. This repetition of characteristics is what makes a function periodic. 🤙
Additionally, periodic functions can be represented by a mathematical equation, such as a sine or cosine function. These equations can be used to model real-world phenomena, such as sound waves, electrical signals, and even the movement of the earth. By understanding the period and other characteristics of a periodic function, we can make predictions and analyze patterns in these phenomena. 🌎
Source: Penn State
<< Hide Menu
Jesse
Jesse
3.1 Periodic Phenomena
Have you hopped on a carousel ride before? 🎠
If so, have you even wondered why you come back to the starting point whenever you complete an entire revolution again, again, and again when you were younger?

Source: Pacific Park
…Or maybe you were in a ferris wheel and you cycle from getting to the top to coming back to the bottom. 🎡
What do carousels and ferris wheels have in common? They’re both examples of periodic phenomena in real life! Now let’s translate this piece of information into the world of precalculus. 🏃
A periodic relationship is a type of mathematical relationship that can be observed between two aspects of a given context. These relationships can be identified by observing a repeating pattern in the output values as the input values increase over successive, equal length intervals. 🔄 The output values will repeat this pattern at regular intervals, hence the name "periodic relationship."
One way to visualize a periodic relationship is through the use of a graph. A graph is a visual representation of a mathematical relationship, and it can be used to illustrate the repeating pattern of a periodic relationship. By plotting the input and output values on a graph, the repeating pattern of the relationship can be clearly observed.

Source: Byjus
🔀 Periods = Cycles
It is important to note that the graph of a periodic relationship can be constructed from the graph of a single cycle of the relationship. This is because the repeating pattern of a periodic relationship is consistent across all cycles, meaning that the shape of the graph will be the same for each cycle. By analyzing the graph of a single cycle, one can understand the overall behavior of the periodic relationship. 🔘
The period of a function is a key concept in understanding periodic relationships. It is defined as the smallest positive value of k for which the function f(x + k) is equal to f(x) for all x in the domain of the function.

Source: Math Warehouse
One important property of a periodic function is that it can be completely determined by any interval of width k. This means that if we know the behavior of the function over a single interval of width k, we can deduce the behavior of the function over any other interval of the same width. This is because the function will repeat its behavior over these intervals with the same pattern.
For example, if we know the behavior of the function f(x) over the interval [0, k], we can deduce the behavior of the function over the interval [k, 2k] and so on. This is because the function will repeat its behavior over the interval [k, 2k] with the same pattern as it did over the interval [0,k].
It is also important to note that a function can have multiple periods. ♾️ For example, if a function has a period of 4, it also has a period of 8, 12, etc. But the smallest period is called the fundamental period (no need to remember for the AP exam).
In order to estimate the period of a function, one can investigate successive equal-length output values and look for patterns that repeat. Once a repeating pattern is found, the length of that pattern can be considered the period of the function! 📐
🌐 Other Properties: Concavities & Rates of Change
Periodic functions also have other characteristics, such as intervals of increase and decrease, different concavities, and various rates of change. However, unlike non-periodic functions, these characteristics will be consistent throughout all periods of the function. 🎓
For example, if a periodic function has an interval of increase in the first period, it will also have an interval of increase in every subsequent period. This repetition of characteristics is what makes a function periodic. 🤙
Additionally, periodic functions can be represented by a mathematical equation, such as a sine or cosine function. These equations can be used to model real-world phenomena, such as sound waves, electrical signals, and even the movement of the earth. By understanding the period and other characteristics of a periodic function, we can make predictions and analyze patterns in these phenomena. 🌎

Source: Penn State

© 2024 Fiveable Inc. All rights reserved.