Browse By Unit
Unit 3 Overview: Trigonometric and Polar Functions
1 min read•june 18, 2024
Jesse
Jesse
3.0 Unit 3 Overview: Trigonometric and Polar Functions
AP Precalculus’ Unit 3 (Trigonometric and Polar Functions) covers a wide range of topics, from the basic trigonometric functions to more advanced topics such as polar coordinates and inverse trigonometric functions. 🔄 Similar to the other two units seen so far, this unit focuses on using these concepts to (1) analyze and model real-world phenomena and (2) solve problems in mathematics and other areas.
One might wonder, “How do these concepts apply to real life?” ✋
Interestingly, trigonometric and polar functions have many applications in various fields such as:
- 🧮 Mathematics: Trigonometry is used in many branches of mathematics, such as calculus, geometry, and linear algebra. It is used to find lengths and angles in triangles and circles, as well as to solve equations and inequalities.
- ☢️ Physics: Trigonometry and polar coordinates are used in physics to describe the motion and position of objects in two and three-dimensional space. They are also used in the study of wave motion, such as sound and light waves, and in the study of oscillations and vibrations.
- 🛠 Engineering: Trigonometry and polar coordinates are used in engineering to solve problems involving angles, distances, and positions in two and three-dimensional space. They are used in the fields of mechanical engineering, electrical engineering, and computer graphics.
- 💻 Computer Science: Trigonometry is used in computer graphics to create two-dimensional and three-dimensional images and animations. It is also used in the field of computer vision to detect shapes and patterns in images.
- 🔭 Astronomy: Trigonometry is used in astronomy to find the positions of celestial bodies, such as stars and planets, in the sky. It is also used to calculate the distances between celestial bodies and to predict the movements of celestial bodies over time.
- 💰 Economics: Trigonometry and polar coordinates are used in economics to model and analyze data, such as market trends and consumer behavior. They are used to identify patterns and make predictions about future market conditions.
- 🧬 Biology: Trigonometry is used in biology to study the shapes and structures of living organisms, such as the growth patterns of plants and the movement patterns of animals.
- 🌧 Meteorology: Trigonometry is used in meteorology to study the movement and behavior of weather systems, such as hurricanes, tornadoes, and thunderstorms.
- 🏛 Architecture: Trigonometry is used in architecture to design and construct buildings, bridges, and other structures. It is used to calculate angles, distances, and measurements, and to ensure that structures are stable and secure.
This means that once you grasp the general ideas provided by this unit, you can apply them to virtually (almost) any field you see yourself in five, ten years down the road! ⭐
United Breakdown
🔀 Periodic Phenomena
Periodic phenomena are patterns that repeat over time. They are often modeled using trigonometric functions, such as the sine and cosine functions. In this unit, you will learn how to identify and analyze periodic phenomena, and how to use trigonometric functions to model them. 🎠
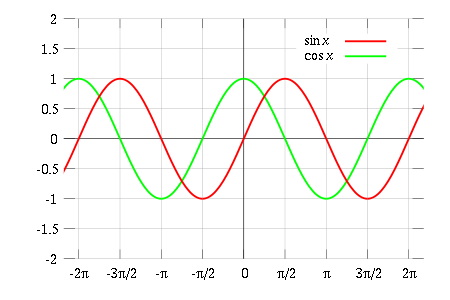
Source: Wikibooks
2️⃣ The Big Two: Sine and Cosine
Likewise, sine and cosine function values are used to find the coordinates of a point on a circle. You will learn how to use the unit circle to find the values of these functions for special angles, and how to use these values to find the coordinates of a point on a circle.
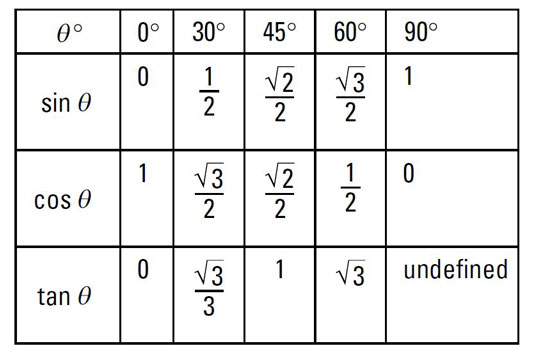
Source: Dummies
Sine and cosine function graphs are used to represent periodic phenomena. You’ll soon learn how to sketch these graphs, and how to analyze them to find the period, amplitude, and vertical shift of a function.
⏺ Sinusoidal Functions and the Tangent Function
Sinusoidal functions are a type of periodic function that can be represented using the sine or cosine function. You will learn how to use these functions to model real-world phenomena, such as sound waves and light waves.
Sinusoidal function transformations are used to change the appearance of a sinusoidal function. You will learn how to use transformations to shift, stretch, and compress a function, and how to use these transformations to model real-world phenomena.
Sinusoidal function context and data modeling are used to analyze real-world data. You will learn how to use sinusoidal functions to model data, and how to use the models to make predictions and analyze patterns in the data. 🤔
To complete the three main trigonometric functions, the tangent function is a trigonometric function that is used to find the slope of a line. ↗️ You will learn how to use the tangent function to find the slope of a line, and how to use it to solve problems involving angles and distances.
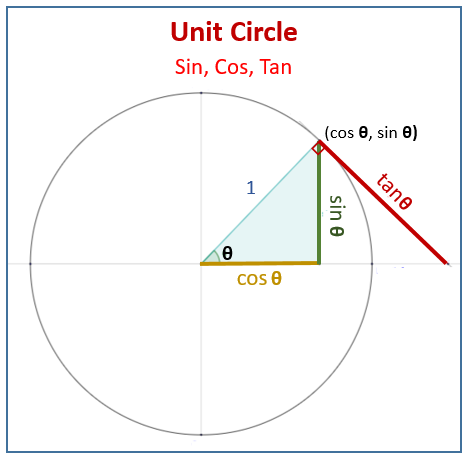
Source: Online Math Learning
⏪ Inverse Trigonometric Functions
Inverse trigonometric functions are used to find the angles that correspond to a given sine, cosine, or tangent value. You will learn how to use these functions to solve problems involving angles and distances. 🏃
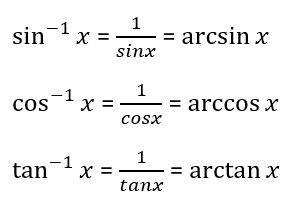
Source: Math Worksheets Center
Trigonometric equations and inequalities are used to solve problems involving angles and distances. You will learn how to use trigonometric functions to solve equations and inequalities, and how to use these solutions to solve problems. 🤓
3️⃣ The Other Three: Secant, Cosecant, and Cotangent
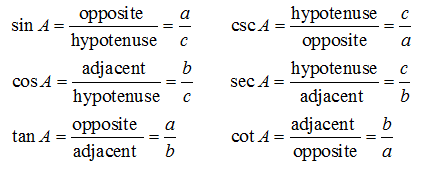
Source: Trig Cheat Sheet
Equivalent representations of trigonometric functions are used to express trigonometric functions in different forms. You will learn how to use identities and trigonometric equations to express a trigonometric function in different forms and how to use them to simplify trigonometric expressions. 🧐
🌀 Polar Coordinates and Functions
Trigonometry and polar coordinates are used to express positions in a plane. You will learn how to use polar coordinates to express positions in a plane and how to use trigonometry to find the distances and angles between points in a plane. ✈️
Polar function graphs are used to represent functions in polar coordinates. You will learn how to sketch and analyze polar function graphs and how to use them to model real-world phenomena.
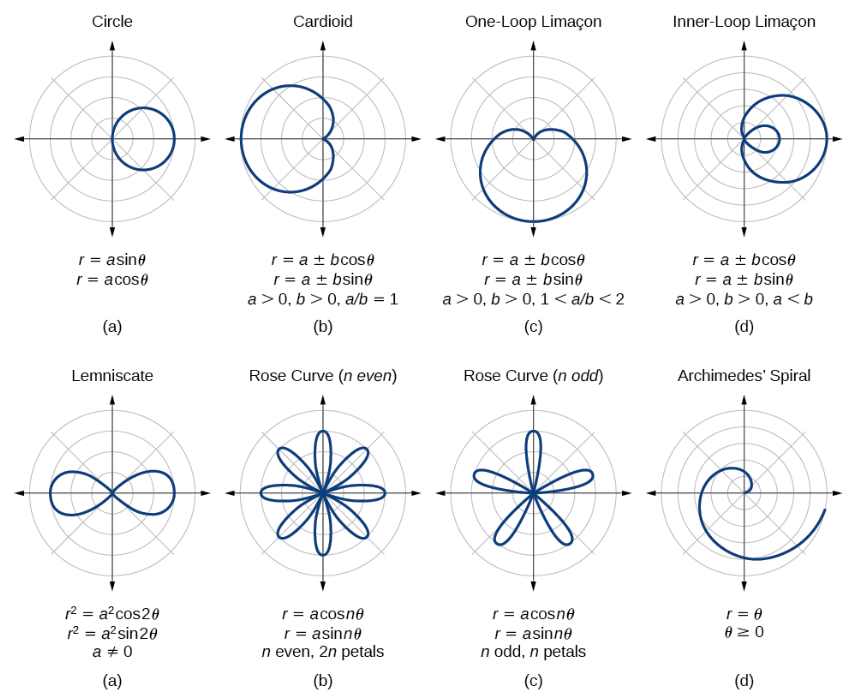
Source: Medium
Rates of change in polar functions are used to describe how the value of a function changes with respect to the angle. You will learn how to use the concept of rates of change in polar functions to analyze and understand how a function behaves in a polar coordinate system.
<< Hide Menu
Unit 3 Overview: Trigonometric and Polar Functions
1 min read•june 18, 2024
Jesse
Jesse
3.0 Unit 3 Overview: Trigonometric and Polar Functions
AP Precalculus’ Unit 3 (Trigonometric and Polar Functions) covers a wide range of topics, from the basic trigonometric functions to more advanced topics such as polar coordinates and inverse trigonometric functions. 🔄 Similar to the other two units seen so far, this unit focuses on using these concepts to (1) analyze and model real-world phenomena and (2) solve problems in mathematics and other areas.
One might wonder, “How do these concepts apply to real life?” ✋
Interestingly, trigonometric and polar functions have many applications in various fields such as:
- 🧮 Mathematics: Trigonometry is used in many branches of mathematics, such as calculus, geometry, and linear algebra. It is used to find lengths and angles in triangles and circles, as well as to solve equations and inequalities.
- ☢️ Physics: Trigonometry and polar coordinates are used in physics to describe the motion and position of objects in two and three-dimensional space. They are also used in the study of wave motion, such as sound and light waves, and in the study of oscillations and vibrations.
- 🛠 Engineering: Trigonometry and polar coordinates are used in engineering to solve problems involving angles, distances, and positions in two and three-dimensional space. They are used in the fields of mechanical engineering, electrical engineering, and computer graphics.
- 💻 Computer Science: Trigonometry is used in computer graphics to create two-dimensional and three-dimensional images and animations. It is also used in the field of computer vision to detect shapes and patterns in images.
- 🔭 Astronomy: Trigonometry is used in astronomy to find the positions of celestial bodies, such as stars and planets, in the sky. It is also used to calculate the distances between celestial bodies and to predict the movements of celestial bodies over time.
- 💰 Economics: Trigonometry and polar coordinates are used in economics to model and analyze data, such as market trends and consumer behavior. They are used to identify patterns and make predictions about future market conditions.
- 🧬 Biology: Trigonometry is used in biology to study the shapes and structures of living organisms, such as the growth patterns of plants and the movement patterns of animals.
- 🌧 Meteorology: Trigonometry is used in meteorology to study the movement and behavior of weather systems, such as hurricanes, tornadoes, and thunderstorms.
- 🏛 Architecture: Trigonometry is used in architecture to design and construct buildings, bridges, and other structures. It is used to calculate angles, distances, and measurements, and to ensure that structures are stable and secure.
This means that once you grasp the general ideas provided by this unit, you can apply them to virtually (almost) any field you see yourself in five, ten years down the road! ⭐
United Breakdown
🔀 Periodic Phenomena
Periodic phenomena are patterns that repeat over time. They are often modeled using trigonometric functions, such as the sine and cosine functions. In this unit, you will learn how to identify and analyze periodic phenomena, and how to use trigonometric functions to model them. 🎠

Source: Wikibooks
2️⃣ The Big Two: Sine and Cosine
Likewise, sine and cosine function values are used to find the coordinates of a point on a circle. You will learn how to use the unit circle to find the values of these functions for special angles, and how to use these values to find the coordinates of a point on a circle.

Source: Dummies
Sine and cosine function graphs are used to represent periodic phenomena. You’ll soon learn how to sketch these graphs, and how to analyze them to find the period, amplitude, and vertical shift of a function.
⏺ Sinusoidal Functions and the Tangent Function
Sinusoidal functions are a type of periodic function that can be represented using the sine or cosine function. You will learn how to use these functions to model real-world phenomena, such as sound waves and light waves.
Sinusoidal function transformations are used to change the appearance of a sinusoidal function. You will learn how to use transformations to shift, stretch, and compress a function, and how to use these transformations to model real-world phenomena.
Sinusoidal function context and data modeling are used to analyze real-world data. You will learn how to use sinusoidal functions to model data, and how to use the models to make predictions and analyze patterns in the data. 🤔
To complete the three main trigonometric functions, the tangent function is a trigonometric function that is used to find the slope of a line. ↗️ You will learn how to use the tangent function to find the slope of a line, and how to use it to solve problems involving angles and distances.

Source: Online Math Learning
⏪ Inverse Trigonometric Functions
Inverse trigonometric functions are used to find the angles that correspond to a given sine, cosine, or tangent value. You will learn how to use these functions to solve problems involving angles and distances. 🏃
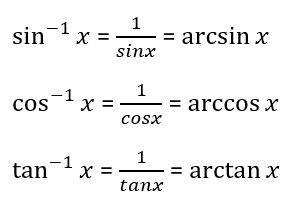
Source: Math Worksheets Center
Trigonometric equations and inequalities are used to solve problems involving angles and distances. You will learn how to use trigonometric functions to solve equations and inequalities, and how to use these solutions to solve problems. 🤓
3️⃣ The Other Three: Secant, Cosecant, and Cotangent
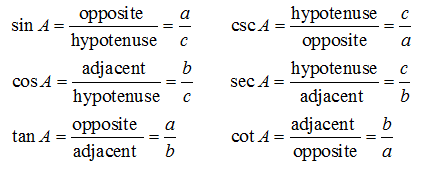
Source: Trig Cheat Sheet
Equivalent representations of trigonometric functions are used to express trigonometric functions in different forms. You will learn how to use identities and trigonometric equations to express a trigonometric function in different forms and how to use them to simplify trigonometric expressions. 🧐
🌀 Polar Coordinates and Functions
Trigonometry and polar coordinates are used to express positions in a plane. You will learn how to use polar coordinates to express positions in a plane and how to use trigonometry to find the distances and angles between points in a plane. ✈️
Polar function graphs are used to represent functions in polar coordinates. You will learn how to sketch and analyze polar function graphs and how to use them to model real-world phenomena.

Source: Medium
Rates of change in polar functions are used to describe how the value of a function changes with respect to the angle. You will learn how to use the concept of rates of change in polar functions to analyze and understand how a function behaves in a polar coordinate system.

© 2024 Fiveable Inc. All rights reserved.