Browse By Unit
3.11 The Secant, Cosecant, and Cotangent Functions
5 min read•june 18, 2024
Kashvi Panjolia
Kashvi Panjolia
So far, you have learned about the three basic trigonometric functions and their inverse functions. In this guide, you will learn about the reciprocal functions of the three trig functions. In trigonometry, the reciprocal functions play a crucial role in understanding the relationships between the different trigonometric functions. The three reciprocal functions are cosecant, secant, and cotangent, denoted by csc(x), sec(x), and cot(x) respectively.
The Cosecant Function
The cosecant function, denoted by csc(x), is a trigonometric function that is defined as the reciprocal of the sine function. In other words, csc(x) = 1/sin(x).

Image courtesy of Wolfram MathWorld.
That's a strange graph! Let's break it down by exploring the main characteristics of the cosecant function. The domain of the cosecant function is all real numbers, except for x = (n+1)𝛑, where n is an integer. These values of x correspond to the vertical asymptotes of the cosecant function, which means that the function becomes infinitely large at every integer multiple of 𝛑, so 2𝛑, 3𝛑, 4𝛑, etc. At every integer multiple of 𝛑, sin(x) = 0, and since cosecant is defined as 1/sin(x), that means we would attempt to compute 1/0, which is not possible. Therefore, we have a vertical asymptote at these values. The range of the cosecant function is (-∞, -1] U [1, ∞).
The period of the cosecant function is 2𝛑, which means that the function repeats every 𝛑 units. This is the same period as the sine function, which makes sense because the cosecant function is defined as the reciprocal of the sine function.
In terms of the unit circle, the cosecant function can be understood as the ratio of the length of the hypotenuse to the length of the y-coordinate. The hypotenuse is always equal to 1, so csc(x) = 1/sin(x) can also be written as csc(x) = 1/y-coordinate. The cosecant function is related to the sine function in that it is the reciprocal of the sine function. In other words, csc(x) = 1/sin(x). This means that when the sine function is at its minimum or maximum values, the cosecant function is at its maximum or minimum values, respectively.
The Secant Function
The secant function, denoted by sec(x), is a trigonometric function that is defined as the reciprocal of the cosine function. In other words, sec(x) = 1/cos(x).
Image courtesy of Wikimedia Commons.
The domain of the secant function is all real numbers, and the range is the set of all real numbers greater than or equal to 1. The secant function has vertical asymptotes at x = (2n + 1)𝛑/2, where n is an integer. This means that the secant function becomes infinitely large at these values of x. The expression (2n + 1) will always yield an odd integer, so the vertical asymptotes of the cosecant function are at 3𝛑/2, 5𝛑/2, 7𝛑/2, etc. As you might have already noticed, these values are where cos(x) = 0, and since we cannot divide 1 by 0, we have a vertical asymptote.
The period of the secant function is 2𝛑, which means that the function repeats every 𝛑 units. This is the same period as the cosine function, which makes sense because the secant function is defined as the reciprocal of the cosine function. In terms of the unit circle, the secant function can be understood as the ratio of the length of the hypotenuse to the length of the x-coordinate. The hypotenuse is always equal to 1, so sec(x) = 1/cos(x) can also be written as sec(x) = 1/x-coordinate.
The secant function is related to the cosine function in that it is the reciprocal of the cosine function. In other words, sec(x) = 1/cos(x). This means that when the cosine function is at its minimum or maximum values, the secant function is at its maximum or minimum values, respectively.
The Cotangent Function
The cotangent function, denoted by cot(x), is a trigonometric function that is defined as the reciprocal of the tangent function. In other words, cot(x) = 1/tan(x).
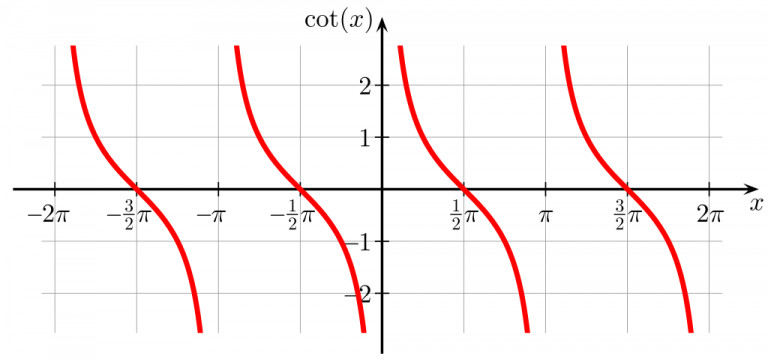
Image courtesy of Voovers.
The domain of the cotangent function is all real numbers, except for **x = (n + 1)**𝛑, where n is an integer. These values of x correspond to the vertical asymptotes of the cotangent function, which means that the function becomes infinitely large at these points. At every integer multiple of 𝛑, the tangent function is 0, so trying to compute 1/0 yields a value that is undefined, and therefore, a vertical asymptote. Also, since tan(x) = sin(x)/cos(x), taking the reciprocal of the function yields cot(x) = cos(x)/sin(x). This also means that when sin(x) = 0, there is a vertical asymptote. The range of the cotangent function is (-∞, -1] U [1, ∞).
The period of the cotangent function is 𝛑, which means that the function repeats every 𝛑 units. This is the same period as the tangent function, which makes sense because the cotangent function is defined as the reciprocal of the tangent function. In terms of the unit circle, the cotangent function can be understood as the ratio of the x-coordinate to the y-coordinate. This means that cot(x) = x-coordinate/y-coordinate.
The cotangent function is related to the tangent function in that it is the reciprocal of the tangent function. In other words, cot(x) = 1/tan(x). This means that when the tangent function is at its minimum or maximum values, the cotangent function is at its maximum or minimum values, respectively. While the tangent function was always increasing, the cotangent function is always decreasing because we took the reciprocal of the tangent function.
** CHOSHACAO: You can use the acronym CHOSHACAO to remember the reciprocal functions. CHO = Cosecant is Hypotenuse over Opposite. SHA = Secant is Hypotenuse over Adjacent. CAO = Cotangent is Adjacent over Hypotenuse. In case you didn't notice, this acronym is the reciprocal of SOHCAHTOA!**
<< Hide Menu
3.11 The Secant, Cosecant, and Cotangent Functions
5 min read•june 18, 2024
Kashvi Panjolia
Kashvi Panjolia
So far, you have learned about the three basic trigonometric functions and their inverse functions. In this guide, you will learn about the reciprocal functions of the three trig functions. In trigonometry, the reciprocal functions play a crucial role in understanding the relationships between the different trigonometric functions. The three reciprocal functions are cosecant, secant, and cotangent, denoted by csc(x), sec(x), and cot(x) respectively.
The Cosecant Function
The cosecant function, denoted by csc(x), is a trigonometric function that is defined as the reciprocal of the sine function. In other words, csc(x) = 1/sin(x).

Image courtesy of Wolfram MathWorld.
That's a strange graph! Let's break it down by exploring the main characteristics of the cosecant function. The domain of the cosecant function is all real numbers, except for x = (n+1)𝛑, where n is an integer. These values of x correspond to the vertical asymptotes of the cosecant function, which means that the function becomes infinitely large at every integer multiple of 𝛑, so 2𝛑, 3𝛑, 4𝛑, etc. At every integer multiple of 𝛑, sin(x) = 0, and since cosecant is defined as 1/sin(x), that means we would attempt to compute 1/0, which is not possible. Therefore, we have a vertical asymptote at these values. The range of the cosecant function is (-∞, -1] U [1, ∞).
The period of the cosecant function is 2𝛑, which means that the function repeats every 𝛑 units. This is the same period as the sine function, which makes sense because the cosecant function is defined as the reciprocal of the sine function.
In terms of the unit circle, the cosecant function can be understood as the ratio of the length of the hypotenuse to the length of the y-coordinate. The hypotenuse is always equal to 1, so csc(x) = 1/sin(x) can also be written as csc(x) = 1/y-coordinate. The cosecant function is related to the sine function in that it is the reciprocal of the sine function. In other words, csc(x) = 1/sin(x). This means that when the sine function is at its minimum or maximum values, the cosecant function is at its maximum or minimum values, respectively.
The Secant Function
The secant function, denoted by sec(x), is a trigonometric function that is defined as the reciprocal of the cosine function. In other words, sec(x) = 1/cos(x).
Image courtesy of Wikimedia Commons.
The domain of the secant function is all real numbers, and the range is the set of all real numbers greater than or equal to 1. The secant function has vertical asymptotes at x = (2n + 1)𝛑/2, where n is an integer. This means that the secant function becomes infinitely large at these values of x. The expression (2n + 1) will always yield an odd integer, so the vertical asymptotes of the cosecant function are at 3𝛑/2, 5𝛑/2, 7𝛑/2, etc. As you might have already noticed, these values are where cos(x) = 0, and since we cannot divide 1 by 0, we have a vertical asymptote.
The period of the secant function is 2𝛑, which means that the function repeats every 𝛑 units. This is the same period as the cosine function, which makes sense because the secant function is defined as the reciprocal of the cosine function. In terms of the unit circle, the secant function can be understood as the ratio of the length of the hypotenuse to the length of the x-coordinate. The hypotenuse is always equal to 1, so sec(x) = 1/cos(x) can also be written as sec(x) = 1/x-coordinate.
The secant function is related to the cosine function in that it is the reciprocal of the cosine function. In other words, sec(x) = 1/cos(x). This means that when the cosine function is at its minimum or maximum values, the secant function is at its maximum or minimum values, respectively.
The Cotangent Function
The cotangent function, denoted by cot(x), is a trigonometric function that is defined as the reciprocal of the tangent function. In other words, cot(x) = 1/tan(x).

Image courtesy of Voovers.
The domain of the cotangent function is all real numbers, except for **x = (n + 1)**𝛑, where n is an integer. These values of x correspond to the vertical asymptotes of the cotangent function, which means that the function becomes infinitely large at these points. At every integer multiple of 𝛑, the tangent function is 0, so trying to compute 1/0 yields a value that is undefined, and therefore, a vertical asymptote. Also, since tan(x) = sin(x)/cos(x), taking the reciprocal of the function yields cot(x) = cos(x)/sin(x). This also means that when sin(x) = 0, there is a vertical asymptote. The range of the cotangent function is (-∞, -1] U [1, ∞).
The period of the cotangent function is 𝛑, which means that the function repeats every 𝛑 units. This is the same period as the tangent function, which makes sense because the cotangent function is defined as the reciprocal of the tangent function. In terms of the unit circle, the cotangent function can be understood as the ratio of the x-coordinate to the y-coordinate. This means that cot(x) = x-coordinate/y-coordinate.
The cotangent function is related to the tangent function in that it is the reciprocal of the tangent function. In other words, cot(x) = 1/tan(x). This means that when the tangent function is at its minimum or maximum values, the cotangent function is at its maximum or minimum values, respectively. While the tangent function was always increasing, the cotangent function is always decreasing because we took the reciprocal of the tangent function.
** CHOSHACAO: You can use the acronym CHOSHACAO to remember the reciprocal functions. CHO = Cosecant is Hypotenuse over Opposite. SHA = Secant is Hypotenuse over Adjacent. CAO = Cotangent is Adjacent over Hypotenuse. In case you didn't notice, this acronym is the reciprocal of SOHCAHTOA!**

© 2024 Fiveable Inc. All rights reserved.