Browse By Unit
Jesse
Jesse
3.2 Sine, Cosine, and Tangent
💆 A Refresher on Geometry
In the coordinate plane, an angle is represented by two rays with a common endpoint, called the vertex. 🔁 An angle is said to be in standard position when the vertex coincides with the origin and one ray coincides with the positive x-axis.

Source: NROC.org
The measure of an angle in standard position is determined by the rotation of the terminal ray from the positive x-axis. ☀️
- Positive angle measures indicate a counterclockwise rotation from the positive x-axis.
- Negative angle measures indicate a clockwise rotation from the positive x-axis.
For example, an angle with a measure of 90 degrees is formed by rotating the terminal ray from the positive x-axis in a counterclockwise direction by 90 degrees.
Additionally, angles in standard position that share a terminal ray differ by an integer number of revolutions. This means that if two angles have the same terminal ray, their angle measures will differ by a multiple of 360 degrees. For example, an angle with a measure of 90 degrees and an angle with a measure of 450 degrees have the same terminal ray and differ by an integer number of revolutions. 📏
Furthermore, the concept of angle measures in standard position is useful when working with trigonometric functions. The sine, cosine, and tangent functions are all defined in terms of angle measures and can be used to calculate the ratio of the sides of a right triangle. 📐
🗣 The Trigonometry Talk
▶️ Radians
The radian measure of an angle in standard position is a unit of measurement used to describe angles in terms of the length of the arc that is subtended by the angle on a circle. It is defined as the ratio of the length of the arc of a circle centered at the origin subtended by the angle to the radius of that same circle. ⭕
For example, if an angle in standard position subtends an arc of length 4 units on a circle with a radius of 2 units, the radian measure of the angle would be 2 (the ratio of 4 to 2).
A key feature of radian measure is that it is independent of the size of the circle. This means that the same angle can have different degrees measure depending on the circle but will always have the same radian measure. 🤔
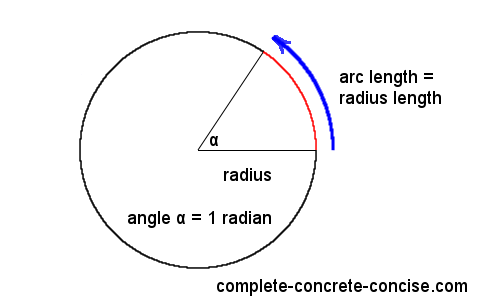
Source: Complete, Concrete, Concise
The radian measure is the most natural way of measuring angles since it is based on the length of the arc, which is a geometric concept, rather than the number of degrees. 🤓
1️⃣ Sine (sin)
Given an angle in standard position and a circle centered at the origin, there is a unique point, P, where the terminal ray of the angle intersects the circle. The sine of the angle is defined as the ratio of the vertical displacement of point P from the x-axis to the distance between the origin and point P. ↕️
This relationship is illustrated in the following formula: sin(θ) = y / r, where θ is the angle in radians, y is the y-coordinate of point P, and r is the radius of the circle. 📕
For a unit circle, which has a radius of 1, the sine of the angle is the y-coordinate of point P. This is because the ratio of the vertical displacement to the radius is equal to the y-coordinate of P, which is the same as the sine of the angle.
The sine function is periodic, with a period of 2π, and it has a range of -1 to 1. This means that the sine of an angle in a unit circle will always be between -1 and 1.
2️⃣ Cosine (cos)
Similar to the sine function, given an angle in standard position and a circle centered at the origin, there is a unique point, P, where the terminal ray of the angle intersects the circle. The cosine of the angle is defined as the ratio of the horizontal displacement of point P from the y-axis to the distance between the origin and point P. ↔️
This relationship is illustrated in the following formula: cos(θ) = x/r, where θ is the angle in radians, x is the x-coordinate of point P, and r is the radius of the circle. 📗
For a unit circle, which has a radius of 1, the cosine of the angle is the x-coordinate of point P. This is because the ratio of the horizontal displacement to the radius is equal to the x-coordinate of P, which is the same as the cosine of the angle.
The cosine function is also periodic, with a period of 2π, and it has a range of -1 to 1. This means that the cosine of an angle in a unit circle will always be between -1 and 1.

Source: Lumen Learning
3️⃣ Tangent (tan)
Given an angle in standard position, the tangent of the angle is defined as the slope of the terminal ray, if it exists. The slope of a line is defined as the ratio of the vertical displacement to the horizontal displacement over any interval. In the case of the terminal ray, the vertical displacement is the y-coordinate of the point at which the terminal ray intersects the unit circle, and the horizontal displacement is the x-coordinate of that same point. ↗️
Therefore, the tangent of the angle is the ratio of the y-coordinate to the x-coordinate of the point at which the terminal ray intersects the unit circle. This relationship is illustrated in the following formula: tan(θ) = y/x, where θ is the angle in radians, y is the y-coordinate of point P, and x is the x-coordinate of point P. 📘
Additionally, it is also the ratio of the angle's sine to its cosine, this relationship is illustrated in the following formula: tan(θ) = sin(θ) / cos(θ) 📙
The tangent function is periodic, with a period of π, and it has no defined range.
<< Hide Menu
Jesse
Jesse
3.2 Sine, Cosine, and Tangent
💆 A Refresher on Geometry
In the coordinate plane, an angle is represented by two rays with a common endpoint, called the vertex. 🔁 An angle is said to be in standard position when the vertex coincides with the origin and one ray coincides with the positive x-axis.

Source: NROC.org
The measure of an angle in standard position is determined by the rotation of the terminal ray from the positive x-axis. ☀️
- Positive angle measures indicate a counterclockwise rotation from the positive x-axis.
- Negative angle measures indicate a clockwise rotation from the positive x-axis.
For example, an angle with a measure of 90 degrees is formed by rotating the terminal ray from the positive x-axis in a counterclockwise direction by 90 degrees.
Additionally, angles in standard position that share a terminal ray differ by an integer number of revolutions. This means that if two angles have the same terminal ray, their angle measures will differ by a multiple of 360 degrees. For example, an angle with a measure of 90 degrees and an angle with a measure of 450 degrees have the same terminal ray and differ by an integer number of revolutions. 📏
Furthermore, the concept of angle measures in standard position is useful when working with trigonometric functions. The sine, cosine, and tangent functions are all defined in terms of angle measures and can be used to calculate the ratio of the sides of a right triangle. 📐
🗣 The Trigonometry Talk
▶️ Radians
The radian measure of an angle in standard position is a unit of measurement used to describe angles in terms of the length of the arc that is subtended by the angle on a circle. It is defined as the ratio of the length of the arc of a circle centered at the origin subtended by the angle to the radius of that same circle. ⭕
For example, if an angle in standard position subtends an arc of length 4 units on a circle with a radius of 2 units, the radian measure of the angle would be 2 (the ratio of 4 to 2).
A key feature of radian measure is that it is independent of the size of the circle. This means that the same angle can have different degrees measure depending on the circle but will always have the same radian measure. 🤔

Source: Complete, Concrete, Concise
The radian measure is the most natural way of measuring angles since it is based on the length of the arc, which is a geometric concept, rather than the number of degrees. 🤓
1️⃣ Sine (sin)
Given an angle in standard position and a circle centered at the origin, there is a unique point, P, where the terminal ray of the angle intersects the circle. The sine of the angle is defined as the ratio of the vertical displacement of point P from the x-axis to the distance between the origin and point P. ↕️
This relationship is illustrated in the following formula: sin(θ) = y / r, where θ is the angle in radians, y is the y-coordinate of point P, and r is the radius of the circle. 📕
For a unit circle, which has a radius of 1, the sine of the angle is the y-coordinate of point P. This is because the ratio of the vertical displacement to the radius is equal to the y-coordinate of P, which is the same as the sine of the angle.
The sine function is periodic, with a period of 2π, and it has a range of -1 to 1. This means that the sine of an angle in a unit circle will always be between -1 and 1.
2️⃣ Cosine (cos)
Similar to the sine function, given an angle in standard position and a circle centered at the origin, there is a unique point, P, where the terminal ray of the angle intersects the circle. The cosine of the angle is defined as the ratio of the horizontal displacement of point P from the y-axis to the distance between the origin and point P. ↔️
This relationship is illustrated in the following formula: cos(θ) = x/r, where θ is the angle in radians, x is the x-coordinate of point P, and r is the radius of the circle. 📗
For a unit circle, which has a radius of 1, the cosine of the angle is the x-coordinate of point P. This is because the ratio of the horizontal displacement to the radius is equal to the x-coordinate of P, which is the same as the cosine of the angle.
The cosine function is also periodic, with a period of 2π, and it has a range of -1 to 1. This means that the cosine of an angle in a unit circle will always be between -1 and 1.

Source: Lumen Learning
3️⃣ Tangent (tan)
Given an angle in standard position, the tangent of the angle is defined as the slope of the terminal ray, if it exists. The slope of a line is defined as the ratio of the vertical displacement to the horizontal displacement over any interval. In the case of the terminal ray, the vertical displacement is the y-coordinate of the point at which the terminal ray intersects the unit circle, and the horizontal displacement is the x-coordinate of that same point. ↗️
Therefore, the tangent of the angle is the ratio of the y-coordinate to the x-coordinate of the point at which the terminal ray intersects the unit circle. This relationship is illustrated in the following formula: tan(θ) = y/x, where θ is the angle in radians, y is the y-coordinate of point P, and x is the x-coordinate of point P. 📘
Additionally, it is also the ratio of the angle's sine to its cosine, this relationship is illustrated in the following formula: tan(θ) = sin(θ) / cos(θ) 📙
The tangent function is periodic, with a period of π, and it has no defined range.

© 2025 Fiveable Inc. All rights reserved.