Browse By Unit
4.12 Linear Transformations and Matrices
1 min read•june 18, 2024
Jesse
Jesse
4.12 Linear Transformations and Matrices
A linear transformation is a function that maps an input vector to an output vector in a way that preserves the operations of vector addition and scalar multiplication. ⚙️ This means that if T is a linear transformation and u and v are vectors in the input space, and c is a scalar, then T(u+v) = T(u) + T(v) and T(cu) = cT(u). 🎁
For a given input vector x, the output vector T(x) can be calculated by multiplying the input vector by the matrix A that represents the linear transformation, such that T(x) = A * x. Each component of the output vector is the sum of constant multiples of the input vector components. This is why the function is called linear, because it preserves the linearity of the input vector. ↕️
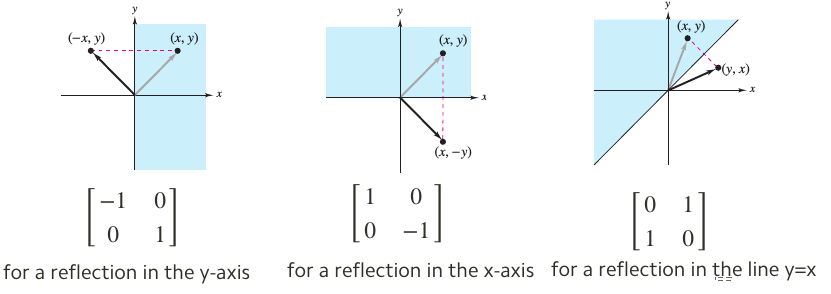
Source: Medium
♾️ Expressing Zero, Single, and n-Vectors
💡 Note: The set of all two-dimensional vectors is denoted R2 in this guide.
One of the key properties of a linear transformation is that it maps the zero vector to the zero vector. 📍 The zero vector, also known as the null vector, is a vector with all components equal to zero, and it is the additive identity of the vector space.
Since a linear transformation preserves the operations of vector addition and scalar multiplication, it follows that T(0) = T(0u) = 0T(u) = 0, where 0 is the scalar zero and u is any vector in the input space. This means that the zero vector will always be mapped to the zero vector under a linear transformation. 0️⃣
A single vector in R2 can be represented as a 2 x 1 matrix, also known as a column vector. A column vector is a matrix that has two rows and one column, and it can be written as [x; y], where x and y are the coordinates of the vector in the x-y plane. This is the standard representation of a vector in R^2. 📓
A set of n vectors in R2 can be represented as a 2 x n matrix, also known as a matrix of column vectors. This matrix is formed by arranging the n column vectors side by side, one after the other. The resulting matrix has two rows and n columns, and it can be written as [v1, v2, ..., vn], where v1, v2, ..., vn are the n column vectors. 📚
Source: Google Sites
✔️ Working Out Linear Transformations
For a linear transformation, L, from R2 to R2, there is a unique 2x2 matrix, A, such that L(v) = Av for vectors in R2. This means that for any vector v in R2, the linear transformation L can be represented by the matrix-vector product Av, where A is a unique 2x2 matrix. This relationship is often referred to as the matrix representation of a linear transformation. 💈
The matrix A, is called the transformation matrix of the linear transformation L. The matrix A contains all the information about the linear transformation L, such as how it stretches, rotates, or reflects the vectors in R2. The matrix A is unique for a given linear transformation L, meaning that different linear transformations will have different matrix representations. 🤔
Conversely, for a given 2x2 matrix A, the function L(v) = Av, is a linear transformation from R2 to R2. This is because the function preserves the operations of vector addition and scalar multiplication, as it holds that L(u + v) = A(u + v) = Au + Av = L(u) + L(v) and L(cu) = A(cu) = c(Au) = cL(u) for any vectors u and v in R2 and any scalar c. ☑️

Source: SlideServe
✖️ Multiplication
Multiplication of a 2 x 2 transformation matrix, A, and a 2 x n matrix of n input vectors, X, gives a 2 x n matrix of the n output vectors for the linear transformation L(v) = Av. This is because the matrix-matrix multiplication follows the distributive property of matrix product, which states that for matrices A, B and C, A(BC) = (AB)C. 🔤
Given a 2x2 transformation matrix A = [a11, a12; a21, a22] and a 2xn matrix of n input vectors X = [v1, v2, ..., vn], the product of the two matrices is given by:
AX = [a11v1 + a12v2, a11v2 + a12v3, ..., a11vn + a12vn; a21v1 + a22v2, a21v2 + a22v3, ..., a21vn + a22vn ]
It's worth noting that each entry of the resulting 2xn matrix represents the output vector of the linear transformation L(v) = Av for each input vector v in X. The resulting matrix has the same number of columns as the input matrix, but the entries of each column are the result of applying the linear transformation to the corresponding input vector. 💯
<< Hide Menu
4.12 Linear Transformations and Matrices
1 min read•june 18, 2024
Jesse
Jesse
4.12 Linear Transformations and Matrices
A linear transformation is a function that maps an input vector to an output vector in a way that preserves the operations of vector addition and scalar multiplication. ⚙️ This means that if T is a linear transformation and u and v are vectors in the input space, and c is a scalar, then T(u+v) = T(u) + T(v) and T(cu) = cT(u). 🎁
For a given input vector x, the output vector T(x) can be calculated by multiplying the input vector by the matrix A that represents the linear transformation, such that T(x) = A * x. Each component of the output vector is the sum of constant multiples of the input vector components. This is why the function is called linear, because it preserves the linearity of the input vector. ↕️

Source: Medium
♾️ Expressing Zero, Single, and n-Vectors
💡 Note: The set of all two-dimensional vectors is denoted R2 in this guide.
One of the key properties of a linear transformation is that it maps the zero vector to the zero vector. 📍 The zero vector, also known as the null vector, is a vector with all components equal to zero, and it is the additive identity of the vector space.
Since a linear transformation preserves the operations of vector addition and scalar multiplication, it follows that T(0) = T(0u) = 0T(u) = 0, where 0 is the scalar zero and u is any vector in the input space. This means that the zero vector will always be mapped to the zero vector under a linear transformation. 0️⃣
A single vector in R2 can be represented as a 2 x 1 matrix, also known as a column vector. A column vector is a matrix that has two rows and one column, and it can be written as [x; y], where x and y are the coordinates of the vector in the x-y plane. This is the standard representation of a vector in R^2. 📓
A set of n vectors in R2 can be represented as a 2 x n matrix, also known as a matrix of column vectors. This matrix is formed by arranging the n column vectors side by side, one after the other. The resulting matrix has two rows and n columns, and it can be written as [v1, v2, ..., vn], where v1, v2, ..., vn are the n column vectors. 📚
Source: Google Sites
✔️ Working Out Linear Transformations
For a linear transformation, L, from R2 to R2, there is a unique 2x2 matrix, A, such that L(v) = Av for vectors in R2. This means that for any vector v in R2, the linear transformation L can be represented by the matrix-vector product Av, where A is a unique 2x2 matrix. This relationship is often referred to as the matrix representation of a linear transformation. 💈
The matrix A, is called the transformation matrix of the linear transformation L. The matrix A contains all the information about the linear transformation L, such as how it stretches, rotates, or reflects the vectors in R2. The matrix A is unique for a given linear transformation L, meaning that different linear transformations will have different matrix representations. 🤔
Conversely, for a given 2x2 matrix A, the function L(v) = Av, is a linear transformation from R2 to R2. This is because the function preserves the operations of vector addition and scalar multiplication, as it holds that L(u + v) = A(u + v) = Au + Av = L(u) + L(v) and L(cu) = A(cu) = c(Au) = cL(u) for any vectors u and v in R2 and any scalar c. ☑️

Source: SlideServe
✖️ Multiplication
Multiplication of a 2 x 2 transformation matrix, A, and a 2 x n matrix of n input vectors, X, gives a 2 x n matrix of the n output vectors for the linear transformation L(v) = Av. This is because the matrix-matrix multiplication follows the distributive property of matrix product, which states that for matrices A, B and C, A(BC) = (AB)C. 🔤
Given a 2x2 transformation matrix A = [a11, a12; a21, a22] and a 2xn matrix of n input vectors X = [v1, v2, ..., vn], the product of the two matrices is given by:
AX = [a11v1 + a12v2, a11v2 + a12v3, ..., a11vn + a12vn; a21v1 + a22v2, a21v2 + a22v3, ..., a21vn + a22vn ]
It's worth noting that each entry of the resulting 2xn matrix represents the output vector of the linear transformation L(v) = Av for each input vector v in X. The resulting matrix has the same number of columns as the input matrix, but the entries of each column are the result of applying the linear transformation to the corresponding input vector. 💯

© 2024 Fiveable Inc. All rights reserved.