Browse By Unit
4.3 Parametric Functions and Rates of Change
1 min read•june 18, 2024
Jesse
Jesse
4.3 Parametric Functions and Rates of Change
A parametric planar motion function describes the movement of an object in a two-dimensional space, such as the x-y plane. Two key characteristics of this type of function that are related to the direction and rate of change of the object are the velocity vector and the acceleration vector. 🎥
The velocity vector represents the direction and magnitude of the object's instantaneous velocity at a given point in time. It is a vector quantity and can be represented by an arrow pointing in the direction of motion, with the length of the arrow indicating the speed of the object. ↗️
The acceleration vector, on the other hand, represents the direction and magnitude of the object's instantaneous acceleration at a given point in time. Like the velocity vector, it is also a vector quantity, but it points in the direction of the change in velocity. ↖️
In addition to these two vectors, the parametric planar motion function also includes the position vector, which describes the object's position in the x-y plane at a given point in time. Together, these vectors provide a complete picture of the object's motion, including its direction, rate of change, and position.
(Note: we’ll talk about vectors in a later section, so hopefully this should make sense down the road!)
🔁 Directions of Motion
When analyzing the planar motion of a particle, considering the x and y components of the motion separately allows us to notice trends in motion. This is because the direction of motion in the x-y plane can be determined by the behavior of the x(t) and y(t) functions independently. 📈
As the parameter (often represented by "t") increases, the direction of motion of the particle can be determined by the behavior of the x(t) and y(t) functions. 🔃
For example, if x(t) is increasing as the parameter t increases, this indicates that the particle is moving to the right. Conversely, if x(t) is decreasing as t increases, the particle is moving to the left. Similarly, if y(t) is increasing as t increases, the particle is moving upward, and if y(t) is decreasing as t increases, the particle is moving downward.

Source: Oregon Tech
The direction of planar motion of a particle can change at different points in the plane and at different values of the parameter t. For example, if x(t) is increasing and y(t) is decreasing, the particle may be moving in a diagonal direction, but as time progresses and the parameter t changes, the x(t) or y(t) function may change its behavior and the direction of motion will change accordingly.
For example, if the x(t) function changes from increasing to decreasing, the velocity vector in the x direction will change from positive to negative, indicating a change in direction of motion. Similarly, if the acceleration vector changes from positive to negative, this indicates a change in the rate of change of velocity, which in turn indicates a change in the direction of motion. ❄️
🔢 Using Different Representative Parametric Functions
A curve in the plane can be represented by different parametric equations, and each equation can describe the motion of a particle along the curve in a different way. 🤯
For example, one parametric equation for a curve may have the parameter t increasing from 0 to 1 as the particle moves along the curve from the starting point to the end point. 1️⃣ Another parametric equation for the same curve may have the parameter t decreasing from 1 to 0 as the particle moves along the curve in the opposite direction. This will result in different parametric functions for the same curve.
Different parametric functions may also have different velocity and acceleration vectors, which will result in different directions of motion along the same curve!
For example, if the parameter t increases as the particle moves along the curve in one parametric equation, the velocity and acceleration vectors will point in the direction of motion, but if the parameter t decreases, the direction of the velocity and acceleration vectors will be opposite to the direction of motion. 🫡
⏮ Average Rates of Change
Over a given interval [t1, t2] within the domain, the average rate of change can be computed for x(t) and y(t) independently. The ratio of the average rate of change of y to the average rate of change of x gives the slope of the graph between the points on the curve corresponding to t1 and t2, so long as the average rate of change of x(t) ≠ 0. 🚵
To compute the average rate of change of a function over a given interval [t1, t2], you can use the formula:
(f(t2) - f(t1)) / (t2 - t1)
This formula gives the average rate of change of the function f(t) over the interval [t1, t2]. Applying this formula to x(t) and y(t) independently, you can compute the average rate of change of x(t) and y(t) over the interval [t1, t2]. #️⃣
The slope of the graph between the points on the curve corresponding to t1 and t2 is defined as the ratio of the change in y to the change in x, or the ratio of the average rate of change of y to the average rate of change of x, as long as the average rate of change of x is not equal to zero.
This can be also be written as (Δy/Δx) = (y(t2) - y(t1)) / (x(t2) - x(t1). ✅
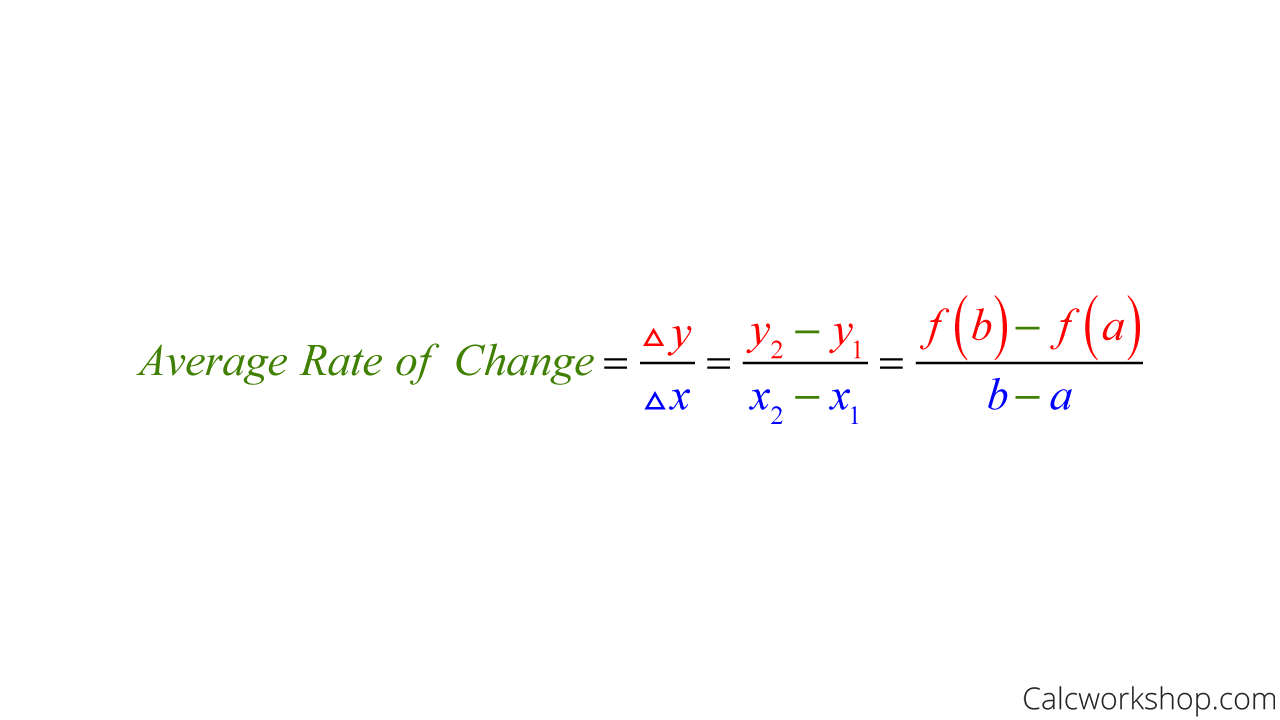
Source: Calcworkshop
<< Hide Menu
4.3 Parametric Functions and Rates of Change
1 min read•june 18, 2024
Jesse
Jesse
4.3 Parametric Functions and Rates of Change
A parametric planar motion function describes the movement of an object in a two-dimensional space, such as the x-y plane. Two key characteristics of this type of function that are related to the direction and rate of change of the object are the velocity vector and the acceleration vector. 🎥
The velocity vector represents the direction and magnitude of the object's instantaneous velocity at a given point in time. It is a vector quantity and can be represented by an arrow pointing in the direction of motion, with the length of the arrow indicating the speed of the object. ↗️
The acceleration vector, on the other hand, represents the direction and magnitude of the object's instantaneous acceleration at a given point in time. Like the velocity vector, it is also a vector quantity, but it points in the direction of the change in velocity. ↖️
In addition to these two vectors, the parametric planar motion function also includes the position vector, which describes the object's position in the x-y plane at a given point in time. Together, these vectors provide a complete picture of the object's motion, including its direction, rate of change, and position.
(Note: we’ll talk about vectors in a later section, so hopefully this should make sense down the road!)
🔁 Directions of Motion
When analyzing the planar motion of a particle, considering the x and y components of the motion separately allows us to notice trends in motion. This is because the direction of motion in the x-y plane can be determined by the behavior of the x(t) and y(t) functions independently. 📈
As the parameter (often represented by "t") increases, the direction of motion of the particle can be determined by the behavior of the x(t) and y(t) functions. 🔃
For example, if x(t) is increasing as the parameter t increases, this indicates that the particle is moving to the right. Conversely, if x(t) is decreasing as t increases, the particle is moving to the left. Similarly, if y(t) is increasing as t increases, the particle is moving upward, and if y(t) is decreasing as t increases, the particle is moving downward.

Source: Oregon Tech
The direction of planar motion of a particle can change at different points in the plane and at different values of the parameter t. For example, if x(t) is increasing and y(t) is decreasing, the particle may be moving in a diagonal direction, but as time progresses and the parameter t changes, the x(t) or y(t) function may change its behavior and the direction of motion will change accordingly.
For example, if the x(t) function changes from increasing to decreasing, the velocity vector in the x direction will change from positive to negative, indicating a change in direction of motion. Similarly, if the acceleration vector changes from positive to negative, this indicates a change in the rate of change of velocity, which in turn indicates a change in the direction of motion. ❄️
🔢 Using Different Representative Parametric Functions
A curve in the plane can be represented by different parametric equations, and each equation can describe the motion of a particle along the curve in a different way. 🤯
For example, one parametric equation for a curve may have the parameter t increasing from 0 to 1 as the particle moves along the curve from the starting point to the end point. 1️⃣ Another parametric equation for the same curve may have the parameter t decreasing from 1 to 0 as the particle moves along the curve in the opposite direction. This will result in different parametric functions for the same curve.
Different parametric functions may also have different velocity and acceleration vectors, which will result in different directions of motion along the same curve!
For example, if the parameter t increases as the particle moves along the curve in one parametric equation, the velocity and acceleration vectors will point in the direction of motion, but if the parameter t decreases, the direction of the velocity and acceleration vectors will be opposite to the direction of motion. 🫡
⏮ Average Rates of Change
Over a given interval [t1, t2] within the domain, the average rate of change can be computed for x(t) and y(t) independently. The ratio of the average rate of change of y to the average rate of change of x gives the slope of the graph between the points on the curve corresponding to t1 and t2, so long as the average rate of change of x(t) ≠ 0. 🚵
To compute the average rate of change of a function over a given interval [t1, t2], you can use the formula:
(f(t2) - f(t1)) / (t2 - t1)
This formula gives the average rate of change of the function f(t) over the interval [t1, t2]. Applying this formula to x(t) and y(t) independently, you can compute the average rate of change of x(t) and y(t) over the interval [t1, t2]. #️⃣
The slope of the graph between the points on the curve corresponding to t1 and t2 is defined as the ratio of the change in y to the change in x, or the ratio of the average rate of change of y to the average rate of change of x, as long as the average rate of change of x is not equal to zero.
This can be also be written as (Δy/Δx) = (y(t2) - y(t1)) / (x(t2) - x(t1). ✅
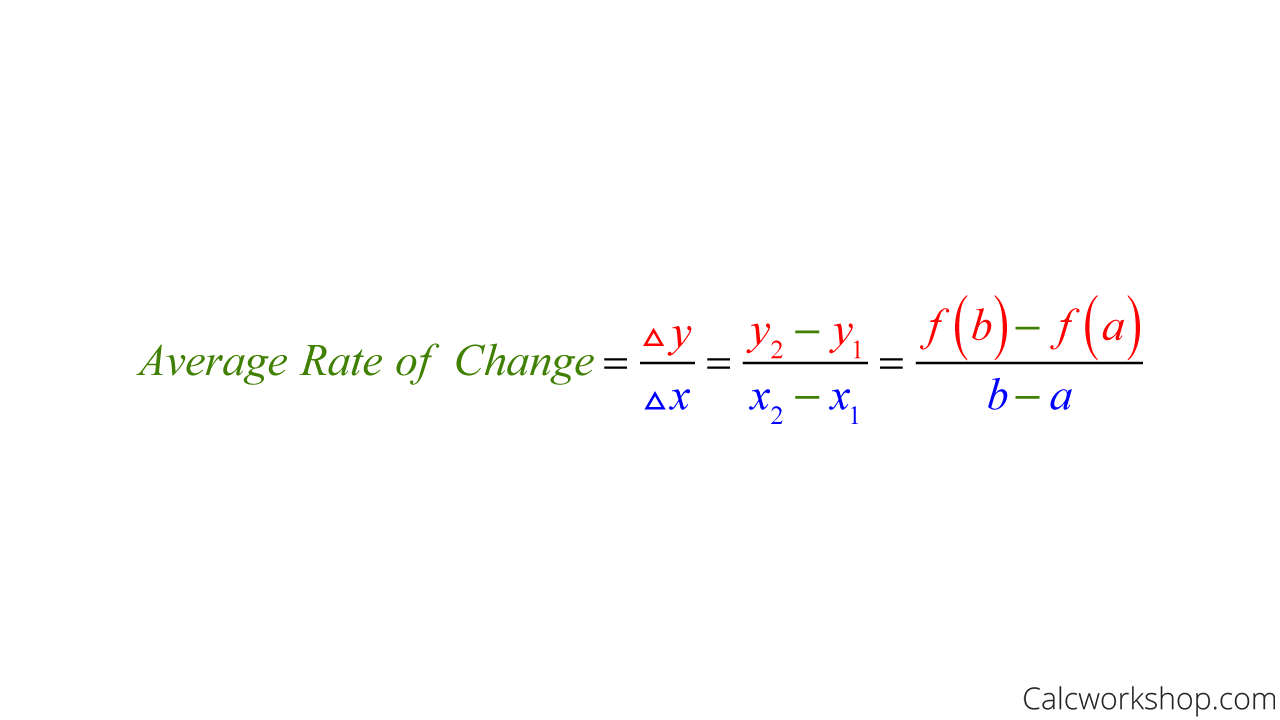
Source: Calcworkshop

© 2024 Fiveable Inc. All rights reserved.