Browse By Unit
4.4 Parametrically Defined Circles and Lines
1 min read•june 18, 2024
Jesse
Jesse
4.4 Parametrically Defined Circles and Lines
A parametrically defined circle is a circle that is defined by a set of parametric equations, rather than by its center and radius. These equations use a parameter, typically denoted by t, to specify the position of a point on the circle as it moves in a counterclockwise direction. 🌀
Similarly, a parametrically defined line is a line that is defined by a set of parametric equations, rather than by its two endpoints. ➖
Fun with Circles
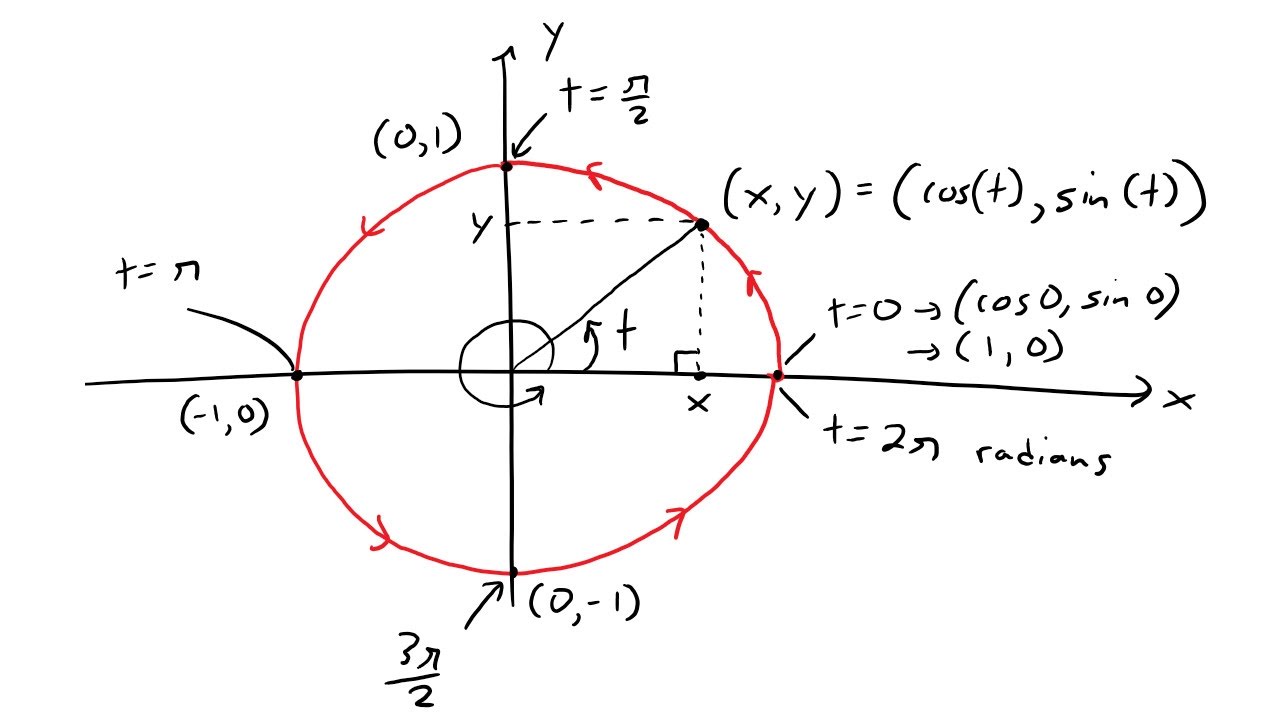
A complete counterclockwise revolution around the unit circle that starts and ends at (1,0) and is centered at the origin can be modeled by the parametric equations (x(t), y(t)) = (cos(t), sin(t)) with the domain 0 ≤ t ≤ 2π.
Source: Math Easy Solutions — YouTube
The equation x(t) = cos(t) represents the x-coordinate of the point on the circle as it moves in a counterclockwise direction. The value of cos(t) ranges from -1 to 1, with cos(0) = 1 and cos(2π) = 1, which corresponds to the starting and ending point (1, 0) on the x-axis.
Similarly, the equation y(t) = sin(t) represents the y-coordinate of the point on the circle as it moves in a counterclockwise direction. The value of sin(t) ranges from -1 to 1, with sin(0) = 0 and sin(2π) = 0, which corresponds to the starting and ending point (1, 0) on the x-axis.
By defining the domain of t to be 0 ≤ t ≤ 2π, we ensure that the point traces out a complete revolution around the unit circle, starting at (1, 0) and ending at (1, 0) again. 🔘
Transformations
The parametric function (x(t), y(t)) = (cos(t), sin(t)) is known as the standard parametric equation for a unit circle centered at the origin. By applying different transformations to this equation, we can model any circular path traversed in the plane. ♻️
For example, to model a circle centered at the point (a, b) with radius r, we can apply the following transformations to the standard equation: (x(t), y(t)) = (a + rcos(t), b + rsin(t))
This transformation shifts the center of the circle from the origin to the point (a,b) and scales the radius from 1 to r. 1️⃣
We can also apply rotation transformation to the standard equation to model a circular path traversed in a different direction. (x(t), y(t)) = (cos(t + c), sin(t + c)), where c is the angle of rotation.
Fun with Lines
A linear path along the line segment from the point (x1, y1) to the point (x2, y2) can be parametrized in many ways, including using an initial position (x1, y1) and rates of change for x with respect to t and y with respect to t. ☂️
One common way to parametrize a linear path is to use the equation of a line in slope-intercept form: y = mx + b, where m is the slope of the line and b is the y-intercept. We can use the two points on the line segment to find the slope (m) of the line and the y-intercept (b). 🤓
We can also parametrize the line segment by using a point on the line (x1, y1) and the direction vector of the line segment, which is given by: (x2 - x1, y2 - y1)
By using this method, we can represent the line segment as the set of all points that can be written as: (x1 + k(x2 - x1), y1 + k(y2 - y1))
Where k is a scalar that varies between 0 and 1. 🫡
In addition, we can also use the parametric equations of the line: x = x1 + k(x2 - x1) y = y1 + k(y2 - y1)
Where k is a scalar that varies between 0 and 1. So, there are many ways to parametrize a linear path along the line segment from the point (x1, y1) to the point (x2, y2) and each one of them has its own advantages and disadvantages! 🌈
<< Hide Menu
4.4 Parametrically Defined Circles and Lines
1 min read•june 18, 2024
Jesse
Jesse
4.4 Parametrically Defined Circles and Lines
A parametrically defined circle is a circle that is defined by a set of parametric equations, rather than by its center and radius. These equations use a parameter, typically denoted by t, to specify the position of a point on the circle as it moves in a counterclockwise direction. 🌀
Similarly, a parametrically defined line is a line that is defined by a set of parametric equations, rather than by its two endpoints. ➖
Fun with Circles
A complete counterclockwise revolution around the unit circle that starts and ends at (1,0) and is centered at the origin can be modeled by the parametric equations (x(t), y(t)) = (cos(t), sin(t)) with the domain 0 ≤ t ≤ 2π.

Source: Math Easy Solutions — YouTube
The equation x(t) = cos(t) represents the x-coordinate of the point on the circle as it moves in a counterclockwise direction. The value of cos(t) ranges from -1 to 1, with cos(0) = 1 and cos(2π) = 1, which corresponds to the starting and ending point (1, 0) on the x-axis.
Similarly, the equation y(t) = sin(t) represents the y-coordinate of the point on the circle as it moves in a counterclockwise direction. The value of sin(t) ranges from -1 to 1, with sin(0) = 0 and sin(2π) = 0, which corresponds to the starting and ending point (1, 0) on the x-axis.
By defining the domain of t to be 0 ≤ t ≤ 2π, we ensure that the point traces out a complete revolution around the unit circle, starting at (1, 0) and ending at (1, 0) again. 🔘
Transformations
The parametric function (x(t), y(t)) = (cos(t), sin(t)) is known as the standard parametric equation for a unit circle centered at the origin. By applying different transformations to this equation, we can model any circular path traversed in the plane. ♻️
For example, to model a circle centered at the point (a, b) with radius r, we can apply the following transformations to the standard equation: (x(t), y(t)) = (a + rcos(t), b + rsin(t))
This transformation shifts the center of the circle from the origin to the point (a,b) and scales the radius from 1 to r. 1️⃣
We can also apply rotation transformation to the standard equation to model a circular path traversed in a different direction. (x(t), y(t)) = (cos(t + c), sin(t + c)), where c is the angle of rotation.
Fun with Lines
A linear path along the line segment from the point (x1, y1) to the point (x2, y2) can be parametrized in many ways, including using an initial position (x1, y1) and rates of change for x with respect to t and y with respect to t. ☂️
One common way to parametrize a linear path is to use the equation of a line in slope-intercept form: y = mx + b, where m is the slope of the line and b is the y-intercept. We can use the two points on the line segment to find the slope (m) of the line and the y-intercept (b). 🤓
We can also parametrize the line segment by using a point on the line (x1, y1) and the direction vector of the line segment, which is given by: (x2 - x1, y2 - y1)
By using this method, we can represent the line segment as the set of all points that can be written as: (x1 + k(x2 - x1), y1 + k(y2 - y1))
Where k is a scalar that varies between 0 and 1. 🫡
In addition, we can also use the parametric equations of the line: x = x1 + k(x2 - x1) y = y1 + k(y2 - y1)
Where k is a scalar that varies between 0 and 1. So, there are many ways to parametrize a linear path along the line segment from the point (x1, y1) to the point (x2, y2) and each one of them has its own advantages and disadvantages! 🌈

© 2024 Fiveable Inc. All rights reserved.